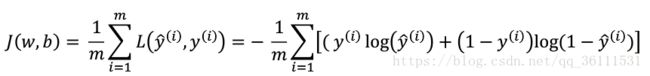算法工程师之路——Deeplearning.ai神经网络与深度学习篇Week2

上一周的回顾

      时间过的很快，转眼又是一周。刚刚过去的一周也是很忙碌，几乎每天都有各种各样工作与生活上的琐事，不过我也在加油努力的学习，毕竟任重而道远嘛！通过与学长学姐的沟通交流，我打算今后的学习采用这样的方式进行：多线程学习法。在学习人工智能领域知识的旅途中，需要涉猎的东西实在是太多太多，比如学习最新的论文，学习别人先进的思想，并尝试着复现；熟练掌握Python、Tensorflow这些人工智能领域常用的工具；学习最新的框架，并在工程项目实践过程加之运用。刚开始接触AI的时候，我喜欢把精力一次放在一个点上，而事实上这样效率并不是非常高，我觉得不管是什么领域的知识，都需要有足够的广度和深度，这样才能在竞争愈发激烈的信息时代站稳脚跟。于是，我计划在学习《神经网络与深度学习》课程的同时，会在文章中总结自己一周看过的论文以及进行过的工程训练，这样多线程的学习方式，不仅提高了学习效率同时也能很好的训练自己的工程与科研能力。继续加油，用这句话来勉励自己和诸君：

书山有路勤为径，学海无涯苦作舟。——《增广贤文》

---

Deeplearning.ai神经网络与深度学习（Week2）

1.1 二分分类与logistic回归

      Binary Classification,即二分分类，是一种非常基础同时又非常重要的监督学习Supervise Learning问题，简单来说就是对样本进行归类，将其归入0类或者1类。举个例子，此时有一张图片，需要我们将其识别出图片中物体是否是猫，如果是，则输出标签1，反之输出0，很好理解。那么问题的关键是，我们应该如何让机器帮我们解决问题呢？答案是logistic回归。
      logistic回归,即逻辑回归，是一种典型的监督学习算法，针对给定的样本，它将帮助输出预测结果为0或者1的标签，更准确的说，是输出预测结果为0或者1的概率。也就是：

      对于给定的样本空间，假设每一个样本都具有n维特征，标签集为[0,1],w为每种特征的权重，b为给定的阈值，那么为了预测出样本标签y，我们利用以下函数进行计算:

$$\hat{y}=w^{T}x+b$$

      需要注意的是，针对多个样本，采用矩阵的形式进行上式的计算。为了得到输出标签为0或1的概率，我们还需要对其进行处理。这里使用一种很经典的sigmoid函数进行处理：

$$s=\sigma (w^T+b)=\sigma (z)=\frac{1}{1+e^{-z}}$$

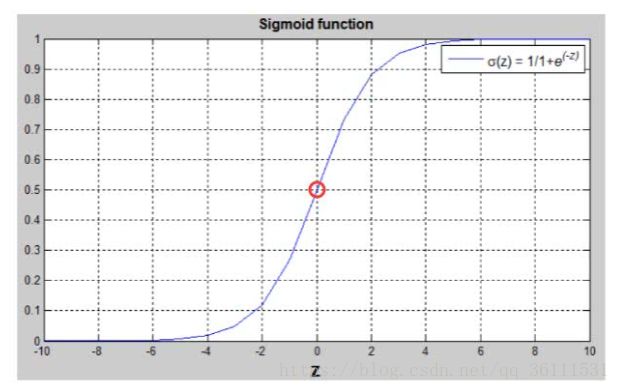
      为什么要用这个函数来处理我们的y值呢？让我们看看sigmoid函数的图像：

      细心的小伙伴可以发现，sigmoid函数的值域是[0,1]，不管你的z值取多少，都可以通过它获得一个大于等于0小于等于1的值，这样就很好的符合了概率的定义。进一步讨论，当通过sigmoid函数处理得到的概率值大于0.5，即z的值大于0时，我们将样本归类为1类（或者说是正类）；相反，当通过sigmoid函数处理得到的概率小于0.5，即z的值小于0时，我们将样本归类为0类（或者说是反类）。
      上文已经提到，我们在进行模型训练时，不会仅采用单个样本进行，训练的对象往往是成千上万个样本，因此，针对多个样本，我们重新给出logistic回归更精确的公式：

$${\hat{y}}^{(i)}=w^T{x}^{(i)}+b$$

      式中的i表示第i个样本，针对每一个样本的每一个特征，我们都需要通过这个公式进行计算。

1.2 logistic回归损失函数与梯度下降法

      显然，通过训练logistic回归模型进行预测得到的结果与真实结果必然存在着一定的误差，我们定义损失函数来度量这个误差值。在统计学习方法中，最小二乘法是度量两个样本距离的一种常用方法，可以用来衡量两个样本之间的相似程度。所以，logistic回归的损失函数可以定义为：

$$L({\hat{y}}^{(i)},y^{(i)})=\frac{1}{2}({\hat{y}}^{(i)}-y^{(i)}{)}^2$$

$$L({\hat{y}}^{(i)},y^{(i)})=-(y^{(i)}log({\hat{y}}^{(i)})+(1-y^{(i)})log(1-{\hat{y}}^{(i)}))$$

      上式为针对单个样本时的计算公式，我们可以发现，当实际样本标签为1时，那么输出标签也应当接近于1才能使损失函数值较小；当实际样本标签为0时，那么输出标签也应当接近于0才能使损失函数较小。
      在单个样本的计算公式基础上，定义成本函数为每个样本损失函数之和，度量回归函数在整个数据集上的误差值：

      为了让我们的logistic回归模型能够更好的去应用在数据集上，我们需要得到最优的w和b值去最小化成本函数的值，使模型更加精准。
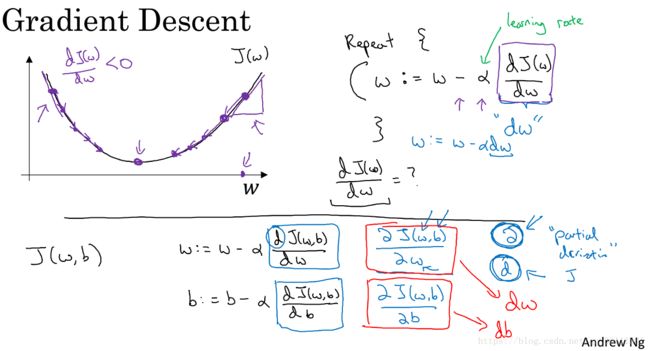
      如何获得最优的w和b呢？需要引入梯度下降法。Gradient Descent，即梯度下降法，其具体含义我不作详细解释，简单来讲就是根据成本函数在某点对w和b的偏导数，动态的对w和b进行更新，直到取得最优解的一种方法：

      通过这样一个对w和b的动态更新过程，我们最终就会得到一个成本函数的最优解。对于m个样本logistic回归的梯度下降计算如下：

      计算的过程运用到了微积分中一个很重要的方法：链式法则。简单来说就是通过一层层的求导和替换，我们可以度量出一个变量通过影响中间变量从而影响另一个变量的影响程度。为了求解导数，我们可以利用一种名为计算图的方法对整个计算过程用流程图进行模拟，并方便找到导数关系。具体计算过程就不再细说，有兴趣的小伙伴可以自己推导一下，会有一些意外收获。

---

论文与工程训练总结

      在学长的建议下，本周我先浏览了深度学习领域综述类文章Recent Advances in Deep Learing，主要讲解了深度学习在近10年里的快速发展，深度神经网络在以非常快的速率持续进步着，科学家们先后提出深度自动编码器、深度卷积神经网络、基于区域卷积神经网络、深度递归网络、循环神经网络、动态记忆网络、长短期记忆网络、增强神经网络等深度学习的神经网络模型。除此之外，还提出了许多深度生成模型，如：波尔曼兹机、深度信念网络、受限波尔曼兹机、深度传感器网络等。训练和优化方式也在发生着很大的改变，Dropout、Maxout、Zoneout、批量正则化、层正则化等等方法在一步步推动着深度学习的发展。我得到的最大感悟就是，以前做建模的时候最多也就用过BP神经网络（不正规的念法）和Elman神经网络，居然还有这么多眼花缭乱的改进神经网络模型，看来确实任重而道远啊。
      工程训练方面，本周完成了实验楼的pandas百题冲关，做的过程感觉很爽，学习了pandas这个常用的Python数据科学库的使用方法，也再加强了我对Python语言的理解。