《数据结构》线段树入门（一）

今天介绍一种非常特殊的数据结构——线段树

首先提出一个问题：


给你n个数，有两种操作：

1：给第i个数的值增加X

2：询问区间[a,b]的总和是什么？

输入描述

输入文件第一行为一个整数n，接下来是n行n个整数，表示格子中原来的整数。接下一个正整数q，再接
下来有q行，表示q个询问，第一个整数表示询问代号，询问代号1表示增加，后面的两个数x和A表示给
位置X上的数值增加A，询问代号2表示区间求和，后面两个整数表示a和b，表示要求[a,b]之间的区间和。

样例输入

4

7 6 3 5

2

1 1 4

2 1 2

样例输出

17

数据范围

1 <= n,q <= 100000

看到这个问题，最朴素的想法是用一个数组模拟，求和时 [ a , b ]中逐个累加 ， 最后输出 。
但是，由于数据量比较大，时间复杂度太高，时间上无法承受。

这时我们可以用线段树( Segment Tree )，这种特殊的数据结构解决这个问题。

那么什么是线段树呢？

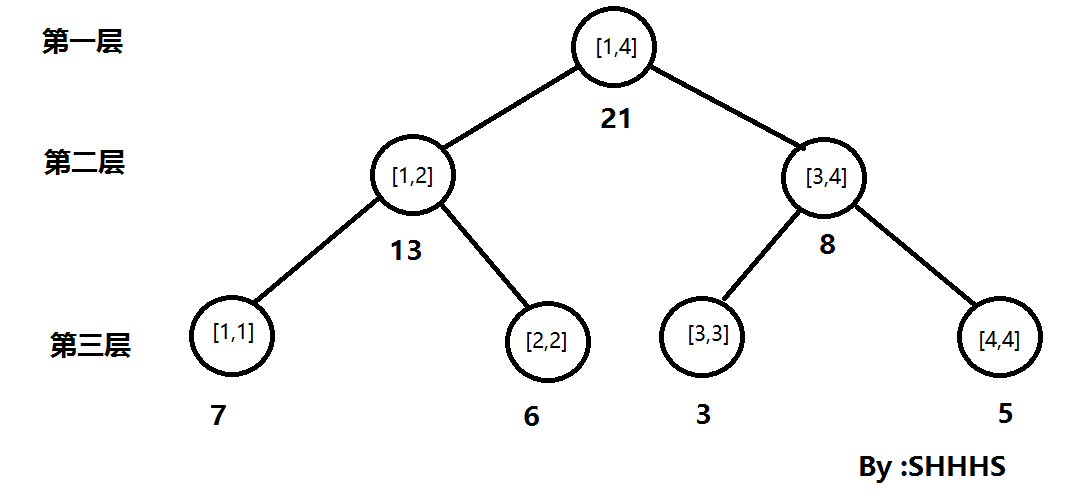
这就是一棵典型的线段树

 

 

一 般的线段树上的每一个节点T[a , b]，代表该节点维护了原数列[ a , b ]区间的信息。对于每一个节点他至少有
三个信息：左端点，右端点，我们需要维护的信息（在本题中我们维护区间和）。由于线段树是一个二叉树，而且是一个平衡二叉树，如果当前结点的编号是i，左端点为L ，右端点为 R ， 那么左儿子的 编号为 i*2 ，左端点为 L ，右端点为 （L + R)/2 ; 同理右儿子的 编号为 i*2+1，左端点为（L+R)/2 ，右端点为 R
。如果当前结点的左端点等于右端点，那么该节点就是叶子节点，直接在该节点赋值即可。显然线段树是递归定义的。

 

线段树就是这样一种数据结构，讲一个大区间分为若干个不相交的区间，每次维护都在小区间上处理，并且查


询也在这些被分解的区间中信息合并出我们需要的结果，这就是线段树高效的原因。

 

线段树的存储：

线段树的存储可用链表和数组模拟。（本文采用数组写法，便于理解）

1.链表存储：

1 struct node
2 {
3     int Left, Right;
4     node *Leftchild , *Rightchild;
5 };

2.数组模拟

1 struct Tree
2 {
3 
4     int l, r;
5     long long sum;
6 
7 } tr[maxN << 2];

注意：数组的空间要开四倍大小，防止访问越界，（理论上大于maxN的最小2x的两倍)

 

建树：

线段树的构建是自顶点而下，即从根节点开始递归构建，根据线段树定义，当左端点等于右端点时（达到递归边界），直接赋值即可，回溯时也要维护区间，代码如下：

 1 void Build_Tree ( int x , int y , int i )
 2 {
 3 
 4     tr[i].l = x;
 5     tr[i].r = y;
 6 
 7     if( x == y )tr[i].sum = a[x] ; //找到叶子节点，赋值
 8 
 9     else
10     {
11         ll mid = (tr[i].l tr[i].r ) >> 1 ;
12 
13         Build_Tree ( x , mid , i << 1); //左子树
14 
15         Build_Tree ( mid + 1 , y , i << 1 | 1); //右子树
16 
17         tr[i].sum = tr[i << 1].sum + tr[i << 1 | 1].sum; //回溯维护区间和
18 
19     }
20 }

 

维护树：

维护树的方法也很好理解，如果目标更新节点在左儿子里，去左儿子中查找；反之，在右儿子中。不断递归，知道找到需要维护的节点，更新它，回溯是一路更新回来。这就是维护的过程，代码如下：

 1 void Update_Tree ( int q , int val , int i )
 2 {
 3     if(tr[i].l == q && tr[i].r == q) //找到需要修改的叶子节点
 4     {
 5         tr[i].sum = val ; //更新当前结点
 6     }
 7     else //当前结点是非叶子结点
 8     {
 9         long long mid = (tr[i].l tr[i].r ) >> 1 ; //取中间
10 
11         if ( q <= mid ) //目标节点在左儿子中
12         {
13             Update_Tree ( q , val , i << 1 );
14         }
15         else if( q > mid ) //目标节点在右儿子中
16         {
17             Update_Tree ( q , val , i << 1 | 1 );
18         }
19         tr[i].sum = tr[i << 1].sum + tr[i << 1 | 1].sum; //回溯
20     }
21 }

 

查询树：

题目中让我们查询区间求和，不难想到如果当前结点的区间完全被目标区间包含，直接返回当前结点的sum值，

否则分类讨论。具体过程通过以下代码理解：

 1 long long Query_Tree ( int q , int w , int i )
 2 {
 3     if ( q <= tr[i].l && w >= tr[i].r ) return tr[i].sum; //当前结点的区间完全被目标区间包含
 4     else
 5     {
 6         long long mid = (tr[i].l tr[i].r) >> 1;
 7         if( q > mid ) //完全在右儿子
 8         {
 9             return Query_Tree ( q , w , i << 1 | 1);
10         }
11         else if (w <= mid ) //完全在左儿子
12         {
13             return Query_Tree ( q , w , i << 1);
14         }
15         else //目标区间在左右都有分布
16         {
17             return Query_Tree ( q , w , i << 1) + Query_Tree ( q , w , i << 1 | 1 );
18         }
19     }
20 }

 

主程序：

 

 1 int main ( )
 2 {
 3 
 4     int N, M, q, val, l, r;
 5     scanf("%d", &N);
 6     for ( int i = 1 ; i <= N ; i++ )scanf("%d", &a[i]);
 7     Build_Tree ( 1 , N , 1);
 8     cin >> M ;
 9     while (M--)
10     {
11         int op ;
12         cin >> op ;
13         if ( op == 1 )
14         {
15             scanf("%d%d", &q, &val);
16             Update_Tree ( q , val , 1);
17         }
18         else
19         {
20             scanf("%d%d", &l, &r);
21             printf("%lld\n", Query_Tree ( l , r, 1 ));
22         }
23     }
24     return 0 ;
25 }

 

线段树的性质：

假设线段树处理的数列长度为N，那么总结点数不超过2*N（满二叉树是最大情况）；

线段分解数量级：线段树能把任意一条长度为M的线段分为不超过2Log2（M）条线段（我们知道一个很大的数，Log一下就变小了），这条性质使线段树的查询与修改复杂度都在O(Log2(n))的范围内解决。

由于线段树是一颗二叉树，深度约为Log2(N)左右。

综上，线段树空间消耗O(n),由于它深度性质，使它在解决问题上有较高的效率。

 

（本期完）

 

 

To Be Continued ;

转载于:https://www.cnblogs.com/shadowland/p/5870339.html