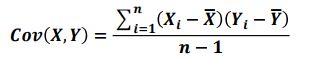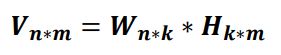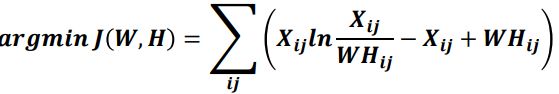Python机器学习应用 Unit2-降维-PCA主成分分析法 和 NMF非负矩阵分解法
> 课源:Python机器学习应用 BIT嵩天,本文作为个人课堂笔记。
主成分分析(PCA )
- 主成分分析(Principal Component Analysis , PCA )是最常用的 一种降维方法,通常用于高维数据集的探索与可视化,还可以用作数 据压缩和预处理等。
- PCA可以把具有相关性的高维变量合成为线性无关的低维变量,称为主成分。主成分能够尽可能保留原始数据的信息。
- 在介绍PCA的原理之前需要回顾涉及到的相关术语: 方差; 协方差 ;协方差矩阵 ;特征向量和特征值。
方差:是各个样本和样本均值的差的平方和的均值,用来度量一组 数据的分散程度。
协方差:用于度量两个变量之间的线性相关性程度,若两个变量的 协方差为0 ,则可认为二者线性无关。协方差矩阵则是由变量的协方差值 构成的矩阵(对称阵)。
特征向量:矩阵的特征向量是描述数据集结构的非零向量,并满足 如下公式:
矩阵的主成分:
就是其协方差矩阵对应的特征向量,按照对应的特征值大小进行排序,最大的特征值就是第一主成分,其次是第二主 成分,以此类推。[可以参考周志华老的西瓜书《机器学习》]
算法过程:
在sklearn库中,可以使用sklearn.decomposition.PCAjn载PCA进行 降维,主要参数有:
- n_components :指定主成分的个数,即降维后数据的维度
- svd_solver :设置特征值分解的方法,默认为’auto',其他可选有 'full' , 'arpack’,’randomized' o
PCA实现高维数据可视化
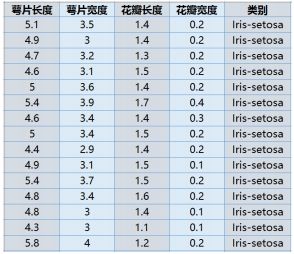
数据下载地址:http://archive.ics.uci.edu/ml/machine-learning-databases/iris/
目标:已知鸢尾花数据是4维的, 共三类样本。使用PCA实现对鸢尾花 数据进行降维,实现在二维平面上的 可视化。
代码部分:
import matplotlib.pyplot as plt
#加载matplotlib用于数据的可视化
from sklearn.decomposition import PCA
#加载PCA算法包
from sklearn.datasets import load_iris
#加载鸢尾花的数据集并导入函数
#加载数据进行降维:
data = load_iris() #以字典的形式加载鸢尾花的数据集
y = data.target #y表示数据集中的标签
X = data.data #X表示数据集中的数据
pca = PCA(n_components=2) #加载PCA算法,设置降维后主成分数量为2
reduced_X = pca.fit_transform(X)#对原始数据进行降维,保存在reduced_X里
#按类别对降维的数据保存:
red_x, red_y = [], [] #第一类数据点
blue_x, blue_y = [], [] #第二类数据点
green_x, green_y = [], [] #第三类数据点
#降维数据的可视化:
for i in range(len(reduced_X)):
if y[i] == 0: #第一类数据点的散点图,下同:
red_x.append(reduced_X[i][0])
red_y.append(reduced_X[i][1])
elif y[i] == 1:
blue_x.append(reduced_X[i][0])
blue_y.append(reduced_X[i][1])
else:
green_x.append(reduced_X[i][0])
green_y.append(reduced_X[i][1])
plt.scatter(red_x, red_y, c='r', marker='x')
plt.scatter(blue_x, blue_y, c='b', marker='D')
plt.scatter(green_x, green_y, c='g', marker='.')
plt.show()
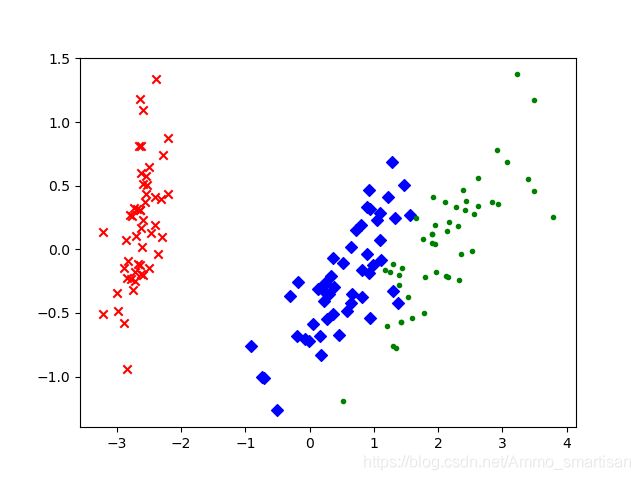
结果分析:可以看出,降维后的数 据仍能够清晰地分成三类。 这样不仅能削减数据的维度, 降低分类任务的工作量,还 能保证分类的质量。
非负矩阵分解(NMF)
非负矩阵分角军(Non-negative Matrix Factorization , NMF ) 是在矩阵中所有元素均为非负数约束条件之下的矩阵分解方法。
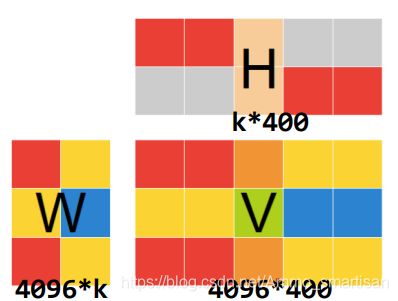
基本思想:给定一个非负矩阵V , NMF能够找到一个非负矩阵W和一个 非负矩阵H ,使得矩阵W和H的乘积近似等于矩阵V中的值。
- W矩阵:基础图像矩阵,相当于从原 矩阵V中抽取出来的特征。
- H矩阵:系数矩阵。
- NMF能够广泛应用于图像分析、文本 挖掘和语音处理等领域。
上图摘自NMF作者的论文,左侧为W矩阵,可以看出从原始图像中抽取出 来的特征,中间的是H矩阵。可以发现乘积结果与原结果是很像的。
矩阵分解优化目标:最小化w矩阵H矩阵的乘积和原始矩阵之间的差 别,目标函数如下:
基于KL散度的优化目标,损失函数如下:
NMF人脸数据特征提取
目标:已知Olivetti人脸数据共 400个,每个数据是64*64大小。由 于N M F分解得到的W矩阵相当于从 原始矩阵中提取的特征,那么就可 以使用N M F对400个人脸数据进行 特征提取。
通过设置k的大小,设置提取的 特征的数目。在本实验中设置k=6 , 随后将提取的特征以图像的形式展示 出来。
代码部分:
#NMF
import matplotlib.pyplot as plt
#加载matplotlib用于数据的可视化
from sklearn import decomposition
#加载PCA算法包
from numpy.random import RandomState
#加载RandomState用于创建随机种子
#设置基本参数并加载数据:
n_row,n_col = 2,3 #设置图像展示的排列情况(2排3列)
n_components = n_row * n_col #设置提取特征值的数目
image_shape = (64,64) #设置人脸数据图片的大小
####
# Load faces data
dataset = fetch_olivetti_faces(shuffle=True, random_state=RandomState(0))
faces = dataset.data
####
def plot_gallery(title, images, n_col=n_col, n_row=n_row):
plt.figure(figsize=(2. * n_col, 2.26 * n_row)) #创建图片并指定图片大小(单位:英寸)
plt.suptitle(title, size=16) #设置标题及字号大小
for i, comp in enumerate(images):
plt.subplot(n_row, n_col, i + 1) #选择画制的子图
vmax = max(comp.max(), -comp.min())
plt.imshow(comp.reshape(image_shape), cmap=plt.cm.gray,
interpolation='nearest',#对数值归一化,
vmin=-vmax, vmax=vmax) #并且以灰度图形显示
plt.xticks(())
plt.yticks(()) #去除子图的坐标轴标签
plt.subplots_adjust(0.01, 0.05, 0.99, 0.94, 0.04, 0.) #对子图位置及间隔调整
plot_gallery("First centered Olivetti faces", faces[:n_components])
####
estimators = [
('Eigenfaces - PCA using randomized SVD',
decomposition.PCA(n_components=6,whiten=True)),
('Non-negative components - NMF',
decomposition.NMF(n_components=6, init='nndsvda', tol=5e-3))
]
####
for name, estimator in estimators:
print("Extracting the top %d %s..." % (n_components, name))
print(faces.shape)
estimator.fit(faces)
components_ = estimator.components_
plot_gallery(name, components_[:n_components])
plt.show()
结果展示: