关于LeetCode中螺旋矩阵 III代码的解析
太久没有编码了,逻辑思维跟不上节奏,阅读别人的代码也费了老半天的劲儿。题目原文在这里。
简要概括题目要求就是输出从方形矩阵中任意位置出发,螺旋遍历矩阵位置并按顺序输出。下面是别人的Python代码:
class Solution(object):
def spiralMatrixIII(self, R, C, r0, c0):
ans = [(r0, c0)]
if R * C == 1: return ans
# For walk length k = 1, 3, 5 ...
for k in xrange(1, 2*(R+C), 2):
# For direction (dr, dc) = east, south, west, north;
# and walk length dk...
for dr, dc, dk in ((0, 1, k), (1, 0, k), (0, -1, k+1), (-1, 0, k+1)):
# For each of dk units in the current direction ...
for _ in xrange(dk):
# Step in that direction
r0 += dr
c0 += dc
# If on the grid ...
if 0 <= r0 < R and 0 <= c0 < C:
ans.append((r0, c0))
if len(ans) == R * C:
return ans这是一段Python2.x的代码。
在Solution类中定义了方法spiralMatrixIII(),列表元素是元组,用于记录遍历位置,初始为(r0,c0),如果是个1x1的矩阵,则直接返回(r0,c0)。接着是循环遍历的语句,下面进行逐句分析。
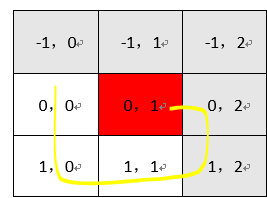
for k in xrange(1, 2*(R+C), 2):xrange()是python2中的函数,如果在python3中请用range(),这里之所以是2*(R+C),是为了包括最坏的情况,也即从除(0,0)之外的其他三个角上出发的情况。下面以2x2的简单情况予以说明:
当(r0,c0)定义为(0,1)的时候,遍历顺序如黄线所示,所以实际执行的时候矩阵已扩展成3x3,这里满足3<(2+2),其他情况类似,读者可自行分析。步进设为2的原因如下:
对一个R*C的矩阵,第一次东南方向走1步,第二次3步,第三次5步……;第一次西北方向2步,第二次4步,第三次6步……。
for dr, dc, dk in ((0, 1, k), (1, 0, k), (0, -1, k+1), (-1, 0, k+1)):这里按顺序分别定义了东、西、南、北四个方向的元组,并且东西方向步数为k,南北方向步数为k+1,
for _ in xrange(dk):
# Step in that direction
r0 += dr
c0 += dc
# If on the grid ...
if 0 <= r0 < R and 0 <= c0 < C:
ans.append((r0, c0))
if len(ans) == R * C:
return ans这里for _ in xrange(dk)实际上就是控制在一个方向上走几步的问题,比如下面的例子:
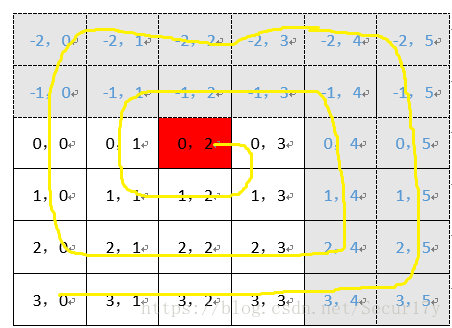
当从(-1,4)到(2,4)后在往西步进,此时对应的应该是(-1,0,4),即后面语句将执行四次,走到(2,0)位置。
由于函数中会判断遍历位置是否属于初始矩阵,所以灰色部分的作标并不会被加入遍历列表ans中,最终当len(ans)=(R+C)时,说明遍历完成。
以上是个人的理解,如有不当还望指正,希望对您有所帮助。