Trie结构

Trie的维基百科

Trie

维基百科，自由的百科全书

跳转到： 导航, 搜索

Trie，又称单词查找树或键树，是一种树形结构，是一种哈希树的变种。典型应用是用于统计和排序大量的字符串（但不仅限于字符串），所以经常被搜索引擎系统用于文本词频统计。它的优点是：最大限度地减少无谓的字符串比较，查询效率比哈希表高。

性质

它有3个基本性质：

1. 根节点不包含字符，除根节点外每一个节点都只包含一个字符。
2. 从根节点到某一节点，路径上经过的字符连接起来，为该节点对应的字符串。
3. 每个节点的所有子节点包含的字符都不相同。

图示

这是一个Trie结构的例子：

在这个Trie结构中，保存了A、to、tea、ted、ten、i、in、inn这8个字符串，仅占用8个字节（不包括指针占用的空间）。

实例

这是一个用于词频统计的程序范例，因使用了getline(3)，所以需要glibc才能链接成功，没有glibc的话可以自行改写。代码由User:JohnBull捐献，遵从GPL版权声明。

#include 
#include 
#include 
 
#define TREE_WIDTH 256
 
#define WORDLENMAX 128
 
struct trie_node_st {
        int count;
        struct trie_node_st *next[TREE_WIDTH];
};
 
static struct trie_node_st root={0, {NULL}};
 
static char *spaces=" \t\n/.\"\'()";
 
static int
insert(const char *word)
{
        int i;
        struct trie_node_st *curr, *newnode;
 
        if (word[0]=='\0') {
                return 0;
        }
        curr = &root;
        for (i=0; ; ++i) {
                if (curr->next[ word[i] ] == NULL) {
                        newnode=(struct trie_node_st*)malloc(sizeof(struct trie_node_st));
                        memset(newnode, 0, sizeof(struct trie_node_st));
                        curr->next[ word[i] ] = newnode;
                }
                if (word[i] == '\0') {
                        break;
                }
                curr = curr->next[ word[i] ];
        }
        curr->count ++;
 
        return 0;
}
 
static void
printword(const char *str, int n)
{
        printf("%s\t%d\n", str, n);
}
 
static int
do_travel(struct trie_node_st *rootp)
{
        static char worddump[WORDLENMAX+1];
        static int pos=0;
        int i;
 
        if (rootp == NULL) {
                return 0;
        }
        if (rootp->count) {
                worddump[pos]='\0';
                printword(worddump, rootp->count);
        }
        for (i=0;inext[i]);
                pos--;
        }
        return 0;
}
 
int
main(void)
{
        char *linebuf=NULL, *line, *word;
        size_t bufsize=0;
        int ret;
 
        while (1) {
                ret=getline(&linebuf, &bufsize, stdin);
                if (ret==-1) {
                        break;
                }
                line=linebuf;
                while (1) {
                        word = strsep(&line, spaces);
                        if (word==NULL) {
                                break;
                        }
                        if (word[0]=='\0') {
                                continue;
                        }
                        insert(word);
                }
        }
 
/* free(linebuf); */
 
        do_travel(&root);
 
        exit(0);
}

隐藏▲ 查  · 论  · 编 计算机科学中的 树 二叉树 二叉树 · 二叉查找树 (BST) · 笛卡尔树 · Top tree · T树   自平衡二叉查找树 AA树 · AVL树 · 红黑树 · 伸展树 · 树堆 · 节点大小平衡树   B树 B树 · B+树 · B*树 · B x树 · UB树 · 2-3树 · 2-3-4树 · (a,b)-树 · Dancing tree · H树   Trie 前缀树 · 后缀树 · 基数树   空间划分树 四叉树 · 八叉树 · k-d树 · vp-树 · R树 · R*树 · R+树 · X树 · M树 · 线段树 · 希尔伯特R树 · 优先R树   非二叉树 Exponential tree  · Fusion tree  · 区间树  · PQ tree  · Range tree  · SPQR tree  · Van Emde Boas tree   其他类型 堆 · 散列树  · Finger tree  · Metric tree  · Cover tree  · BK-tree  · Doubly-chained tree  · iDistance  · Link-cut tree  · 树状数组

Trie

From Wikipedia, the free encyclopedia

Jump to: navigation, search

A trie for keys "A", "to", "tea", "ted", "ten", "i", "in", and "inn".

This article is about a tree data structure. For the French commune, see Trie-sur-Baïse.

In computer science, a trie, or prefix tree, is anordered tree data structure that is used to store an associative array where the keys are usually strings. Unlike a binary search tree, no node in the tree stores the key associated with that node; instead, its position in the tree defines the key with which it is associated. All the descendants of a node have a commonprefix of the string associated with that node, and the root is associated with theempty string. Values are normally not associated with every node, only with leaves and some inner nodes that correspond to keys of interest.

The term trie comes from retrieval. Following the etymology, the inventor, Edward Fredkin, pronounces it /ˈtriː/ "tree".^[1][2] However, it is pronounced /ˈtraɪ/ "try" by other authors.^[1][2][3]

In the example shown, keys are listed in the nodes and values below them. Each complete English word has an arbitrary integer value associated with it. A trie can be seen as adeterministic finite automaton, although the symbol on each edge is often implicit in the order of the branches.

It is not necessary for keys to be explicitly stored in nodes. (In the figure, words are shown only to illustrate how the trie works.)

Though it is most common, tries need not be keyed by character strings. The same algorithms can easily be adapted to serve similar functions of ordered lists of any construct, e.g., permutations on a list of digits or shapes. In particular, abitwise trie is keyed on the individual bits making up a short, fixed size of bits such as an integer number or pointer to memory.

Advantages relative to other search algorithms

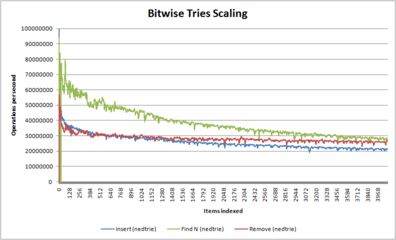
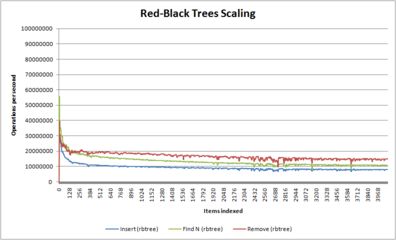
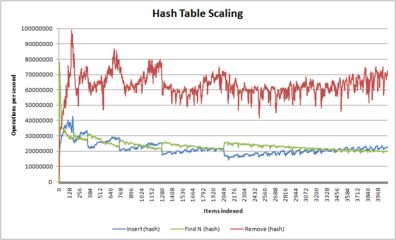
• A series of graphs showing how different algorithms scale with number of items
• 

  Behavior of Fredkin-style tries as a function of size
  (in this case, nedtries, which is an in-place implementation, and therefore has a much steeper curve than a dynamic memory based trie implementation)
  
  

• 

  Behavior of red-black trees as a function of size
  (in this case, the BSD rbtree.h, which shows classic O(log N) behaviour)
  
  

• 

  Behavior of hash tables as a function of size
  (in this case, uthash, which when averaged shows classic O(1) behaviour)
  
  

Unlike most other algorithms, tries have the peculiar feature that the code path, and hence the time required, is almost identical for insert, delete, and find operations. As a result, for situations where code is inserting, deleting and finding in equal measure, tries can handily beat binary search trees, as well as provide a better basis for the CPU's instruction and branch caches.

The following are the main advantages of tries over binary search trees (BSTs):

• Looking up keys is faster. Looking up a key of length m takes worst caseO(m) time. A BST performs O(log(n)) comparisons of keys, wheren is the number of elements in the tree, because lookups depend on the depth of the tree, which is logarithmic in the number of keys if the tree is balanced. Hence in the worst case, a BST takes O(m logn) time. Moreover, in the worst case log(n) will approach m. Also, the simple operations tries use during lookup, such as array indexing using a character, are fast on real machines.
• Tries are more space-efficient when they contain a large number of short keys, since nodes are shared between keys with common initial subsequences.
• Tries facilitate longest-prefix matching.
• The number of internal nodes from root to leaf equals the length of the key. Balancing the tree is therefore of no concern.

The following are the main advantages of tries over hash tables:

• Tries support ordered iteration, whereas iteration over a hash table will result in apseudorandom order given by the hash function (and further affected by the order of hash collisions, which is determined by the implementation).
• Tries facilitate longest-prefix matching, but hashing does not, as a consequence of the above. Performing such a "closest fit" find can, depending on implementation, be as quick as an exact find.
• Tries tend to be faster on average at insertion than hash tables because hash tables must rebuild their index when it becomes full - a very expensive operation. Tries therefore have much better bounded worst-case time costs, which is important for latency-sensitive programs.
• Since no hash function is used, tries are generally faster than hash tables for small keys.

Applications

As replacement of other data structures

As mentioned, a trie has a number of advantages over binary search trees.^[4] A trie can also be used to replace a hash table, over which it has the following advantages:

• Looking up data in a trie is faster in the worst case, O(m) time, compared to an imperfect hash table. An imperfect hash table can have key collisions. A key collision is the hash function mapping of different keys to the same position in a hash table. The worst-case lookup speed in an imperfect hash table is O(N) time, but far more typically is O(1), with O(m) time spent evaluating the hash.
• There are no collisions of different keys in a trie.
• Buckets in a trie which are analogous to hash table buckets that store key collisions are necessary only if a single key is associated with more than one value.
• There is no need to provide a hash function or to change hash functions as more keys are added to a trie.
• A trie can provide an alphabetical ordering of the entries by key.

Tries do have some drawbacks as well:

• Tries can be slower in some cases than hash tables for looking up data, especially if the data is directly accessed on a hard disk drive or some other secondary storage device where the random-access time is high compared to main memory.^[5]
• Some keys, such as floating point numbers, can lead to long chains and prefixes that are not particularly meaningful. Nevertheless a bitwise trie can handle standard IEEE single and double format floating point numbers.

Dictionary representation

A common application of a trie is storing a dictionary, such as one found on amobile telephone. Such applications take advantage of a trie's ability to quickly search for, insert, and delete entries; however, if storing dictionary words is all that is required (i.e. storage of information auxiliary to each word is not required), a minimal acyclic deterministic finite automaton would use less space than a trie. This is because an acyclic deterministic finite automaton can compress identical branches from the trie which correspond to the same suffixes (or parts) of different words being stored.

Tries are also well suited for implementing approximate matching algorithms, including those used inspell checking and hyphenation^[2] software.

Algorithms

We can describe trie lookup (and membership) easily. Given a recursive trie type, storing an optional value at each node, and a list of children tries, indexed by the next character, (here, represented as aHaskell data type):

 data Trie a =
      Trie { value    :: Maybe a
           , children :: [(Char,Trie a)] }

We can look up a value in the trie as follows:

    find :: String -> Trie a -> Maybe a
    find []     t = value t
    find (k:ks) t = case lookup k (children t) of
                        Nothing  -> Nothing
                        Just t'  -> find ks t'

In an imperative style, and assuming an appropriate data type in place, we can describe the same algorithm inPython (here, specifically for testing membership). Note that children is map of a node's children; and we say that a "terminal" node is one which contains a valid word.

def find(node, key):
    for char in key:
        if char not in node.children:
            return None
        else:
            node = node.children[char]
    return node.value

A simple Ruby version:

class Trie
  def initialize
    @root = Hash.new
  end
 
  def build(str) 
    node = @root    
    str.each_char do |ch|
      node[ch] ||= Hash.new
      node = node[ch]
    end
    node[:end] = true
  end
 
  def find(str) 
    node = @root
    str.each_char do |ch|
      return nil unless node = node[ch]
    end
    node[:end] && true
  end
end

A compiling Java version:

public class MinimalExample{
    private interface Node {
        public static final Node EMPTY_NODE = new Node() {
            @Override public String getValue() { return ""; }
            @Override public boolean containsChildValue(char c) { return false; }
            @Override public Node getChild(char c) { return this; }
        };
        public String getValue();
        public boolean containsChildValue(char c);
        public Node getChild(char c);
    }
 
    public Node findValue(Node startNode, String value) {
        Node current = startNode;
        for (char c : value.toCharArray()) {
            if (current.containsChildValue(c)) {
                current = current.getChild(c);
            } else {
                current = Node.EMPTY_NODE;
                break;
            }
        }
        return current;
    }
}

Sorting

Lexicographic sorting of a set of keys can be accomplished with a simple trie-based algorithm as follows:

• Insert all keys in a trie.
• Output all keys in the trie by means of pre-order traversal, which results in output that is in lexicographically increasing order. Pre-order traversal is a kind of depth-first traversal. In-order traversal is another kind of depth-first traversal that is more appropriate for outputting the values that are in abinary search tree rather than a trie.

This algorithm is a form of radix sort.

A trie forms the fundamental data structure of Burstsort, currently (2007) the fastest known, memory/cache-based, string sorting algorithm.^[6]

A parallel algorithm for sorting N keys based on tries is O(1) if there are N processors and the lengths of the keys have a constant upper bound. There is the potential that the keys might collide by having common prefixes or by being identical to one another, reducing or eliminating the speed advantage of having multiple processors operating in parallel.

Full text search

A special kind of trie, called a suffix tree, can be used to index all suffixes in a text in order to carry out fast full text searches.

Bitwise tries

Bitwise tries are much the same as a normal character based trie except that individual bits are used to traverse what effectively becomes a form of binary tree. Generally, implementations use a special CPU instruction to very quickly find the first set bit in a fixed length key (e.g. GCC's __builtin_clz() intrinsic). This value is then used to index a 32 or 64 entry table which points to the first item in the bitwise trie with that number of leading zero bits. The search then proceeds by testing each subsequent bit in the key and choosing child[0] or child[1] appropriately until the item is found.

Although this process might sound slow, it is very cache-local and highly parallelizable due to the lack of register dependencies and therefore in fact has excellent performance on modern out-of-order execution CPUs. Ared-black tree for example performs much better on paper, but is highly cache-unfriendly and causes multiple pipeline andTLB stalls on modern CPUs which makes that algorithm bound by memory latency rather than CPU speed. In comparison, a bitwise trie rarely accesses memory and when it does it does so only to read, thus avoiding SMP cache coherency overhead, and hence is becoming increasingly the algorithm of choice for code which does a lot of insertions and deletions such as memory allocators (e.g. recent versions of the famousDoug Lea's allocator (dlmalloc) and its descendents).

A reference implementation of bitwise tries in C and C++ useful for further study can be found athttp://www.nedprod.com/programs/portable/nedtries/.

Compressing tries

When the trie is mostly static, i.e. all insertions or deletions of keys from a prefilled trie are disabled and only lookups are needed, and when the trie nodes are not keyed by node specific data (or if the node's data is common) it is possible to compress the trie representation by merging the common branches.^[7] This application is typically used for compressing lookup tables when the total set of stored keys is very sparse within their representation space.

For example it may be used to represent sparse bitsets (i.e. subsets of a much fixed enumerable larger set) using a trie keyed by the bit element position within the full set, with the key created from the string of bits needed to encode the integral position of each element. The trie will then have a very degenerate form with many missing branches, and compression becomes possible by storing the leaf nodes (set segments with fixed length) and combining them after detecting the repetition of common patterns or by filling the unused gaps.

Such compression is also typically used in the implementation of the various fast lookup tables needed to retrieveUnicode character properties (for example to represent case mapping tables, or lookup tables containing the combination of base and combining characters needed to support Unicode normalization). For such application, the representation is similar to transforming a very large unidimensional sparse table into a multidimensional matrix, and then using the coordinates in the hyper-matrix as the string key of an uncompressed trie. The compression will then consist of detecting and merging the common columns within the hyper-matrix to compress the last dimension in the key; each dimension of the hypermatrix stores the start position within a storage vector of the next dimension for each coordinate value, and the resulting vector is itself compressible when it is also sparse, so each dimension (associated to a layer level in the trie) is compressed separately.

Some implementations do support such data compression within dynamic sparse tries and allow insertions and deletions in compressed tries, but generally this has a significant cost when compressed segments need to be split or merged, and some tradeoff has to be made between the smallest size of the compressed trie and the speed of updates, by limiting the range of global lookups for comparing the common branches in the sparse trie.

The result of such compression may look similar to trying to transform the trie into adirected acyclic graph (DAG), because the reverse transform from a DAG to a trie is obvious and always possible, however it is constrained by the form of the key chosen to index the nodes.

Another compression approach is to "unravel" the data structure into a single byte array.^[8] This approach eliminates the need for node pointers which reduces the memory requirements substantially and makes memory mapping possible which allows the virtual memory manager to load the data into memory very efficiently.

Another compression approach is to "pack" the trie.^[2] Liang describes a space-efficient implementation of a sparse packed trie applied to hyphenation, in which the descendants of each node may be interleaved in memory.

See also

• Radix tree
• Directed acyclic word graph (aka DAWG)
• Ternary search tries
• Acyclic deterministic finite automata
• Hash trie
• Deterministic finite automata
• Judy array
• Search algorithm
• Extendible hashing
• Hash array mapped trie
• Prefix Hash Tree
• Burstsort
• Luleå algorithm
• Huffman coding
• Ctrie

External links

• NIST's Dictionary of Algorithms and Data Structures: Trie
• Trie implementation and visualisation in flash
• Tries by Lloyd Allison
• Using Tries Topcoder tutorial
• An Implementation of Double-Array Trie
• de la Briandais Tree^{[dead link]}
• Discussing a trie implementation in Lisp
• ServerKit "parse trees" implement a form of Trie in C
• A simple implementation of Trie in Python
• A Trie implemented in Ruby
• A reference implementation of bitwise tries in C and C++
• A reference implementation in Java
• A quick tutorial on TRIE in Java and C++
• A compact C implementation of Judy Tries
• Data::Trie andTree::Trie Perl implementations.

References

1. ^ ^{a b} Black, Paul E. (2009-11-16)."trie". Dictionary of Algorithms and Data Structures. National Institute of Standards and Technology. Archived from the original on 2010-05-19.
2. ^ ^{a b c d} Franklin Mark Liang (1983).Word Hy-phen-a-tion By Com-put-er (Doctor of Philosophy thesis). Stanford University. Archived fromthe original on 2010-05-19. Retrieved 2010-03-28.
3. ^Knuth, Donald (1997). "6.3: Digital Searching".The Art of Computer Programming Volume 3: Sorting and Searching (2nd ed.). Addison-Wesley. p. 492.ISBN 0-201-89685-0.
4. ^Bentley, Jon; Sedgewick, Robert (1998-04-01). "Ternary Search Trees". Dr. Dobb's Journal (Dr Dobb's). Archived fromthe original on 2008-06-23.
5. ^Edward Fredkin (1960). "Trie Memory".Communications of the ACM 3 (9): 490–499. DOI:10.1145/367390.367400.
6. ^"Cache-Efficient String Sorting Using Copying" (PDF). Retrieved 2008-11-15.
7. ^Jan Daciuk, Stoyan Mihov, Bruce W. Watson, Richard E. Watson (2000)."Incremental Construction of Minimal Acyclic Finite-State Automata". Computational Linguistics (Association for Computational Linguistics)26: 3. DOI:10.1162/089120100561601. Archived fromthe original on 2006-03-13. Retrieved 2009-05-28. "This paper presents a method for direct building of minimal acyclic finite states automaton which recognizes a given finite list of words in lexicographical order. Our approach is to construct a minimal automaton in a single phase by adding new strings one by one and minimizing the resulting automaton on-the-fly"
8. ^Ulrich Germann, Eric Joanis, Samuel Larkin (2009)."Tightly packed tries: how to fit large models into memory, and make them load fast, too" (PDF).ACL Workshops: Proceedings of the Workshop on Software Engineering, Testing, and Quality Assurance for Natural Language Processing. Association for Computational Linguistics. pp. 31–39. "We present Tightly Packed Tries (TPTs), a compact implementation of read-only, compressed trie structures with fast on-demand paging and short load times. We demonstrate the benefits of TPTs for storing n-gram back-off language models and phrase tables forstatistical machine translation. Encoded as TPTs, these databases require less space than flat text file representations of the same data compressed with the gzip utility. At the same time, they can be mapped into memory quickly and be searched directly in time linear in the length of the key, without the need to decompress the entire file. The overhead for local decompression during search is marginal."

• de la Briandais, R. (1959). "File Searching Using Variable Length Keys".Proceedings of the Western Joint Computer Conference: 295–298.

[hide] v t e Trees in computer science Binary trees Binary search tree (BST) Cartesian tree Top tree T-tree   Self-balancing binary search trees AA tree AVL tree LLRB tree Red–black tree Scapegoat tree Splay tree Treap   B-trees B+ tree B*-tree Bx-tree UB-tree 2-3 tree 2-3-4 tree (a,b)-tree Dancing tree Htree   Tries Suffix tree Radix tree Ternary search tree X-fast trie Y-fast trie   Binary space partitioning (BSP) trees Quadtree Octree k-d tree Implicitk-d tree vp-tree   Non-binary trees Exponential tree Fusion tree Interval tree PQ tree Range tree SPQR tree Van Emde Boas tree   Spatial data partitioning trees R-tree R+ tree R* tree X-tree M-tree Segment tree Hilbert R-tree Priority R-tree   Other trees Heap Hash tree Finger tree Metric tree Cover tree BK-tree Doubly chained tree iDistance Link-cut tree Fenwick tree