「重磅好文」你能找到的最详细约瑟夫环的数学推导!
文章目录
- 问题描述
- 解法
- 数学推导
- 代码
问题描述
约瑟夫环问题是这样的:
0, 1, …, n - 1 这 n 个数字排成一个圆圈,从数字 0 开始,每次从这个圆圈里删除第 m 个数字。求出这个圆圈里剩下的最后一个数字。
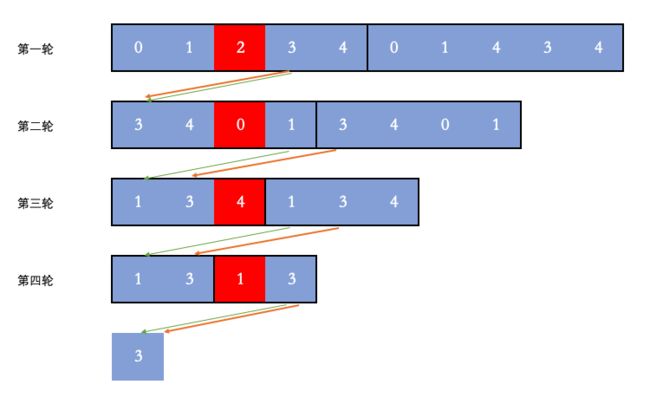
例如,0、1、2、3、4 这 5 个数字组成一个圆圈,从数字 0 开始每次删除第 3 个数字,则删除的前 4 个数字依次是 2、0、4、1,因此最后剩下的数字是 3。如下图所示。
解法
解决约瑟夫环问题,我们采用倒推,我们倒推出:最后剩下的这个数字,在最开始的数组中的位置。
- 剩下最后一个数字(简称“它”)的时候,总个数为 1,它的位置 pos = 0。
- 那么它在上一轮也是安全的,总个数为 2,它的位置 pos = (0 + m) % 2;
- 那么它在上上轮也是安全的,总个数为 3,它的位置 pos = ((0 + m) % 2 + m) % 3;
- 那么它在上上上轮也是安全的,总个数为 4,它的位置 pos = (((0 + m) % 2 + m) % 3) % 4;
- …
- 那么它在游戏开始的第一轮也是安全的,总个数为 n,它的位置 pos 就是最后的结果。
即如果从下向上反推的时候:假如它前一轮的索引为 pos,那么当前轮次的位置就是 (pos + m) % 当前轮次的人数。
最后,由于给出的数字是 nums = 0, 1, 2, …, n - 1,即 nums[i] = i,因此找出 pos 就相当于找到这个数字。
大部分解法解到这里就结束了,缺乏递推公式的数学证明,现就数学推导说明如下。
数学推导
定义:
- 约瑟夫环操作:把一些数字排成一个圆圈,从数字 0 开始,每次从这个圆圈里删除第 m 个数字,直到最后只剩一个数字。
- 函数 f(n, m) :表示对 n 个数字 0, 1, …, n - 1 做约瑟夫环操作,最后剩下的这个数字。(这个定义特别重要,理解之后才向下看)
下面开始推导。
整体思路:
在以 0 为起始的长度为 n 的序列上做约瑟夫环操作的最终结果 f(n, m) =
在完成上轮操作删除数字 k 之后的新序列上的约瑟夫环操作的最终结果 h(n - 1, m) =
将新序列映射成以 0 为起始的长度为 n - 1 的序列上的约瑟夫环操作的最终结果 f(n - 1, m) 的逆映射。
- 得到下次操作的新序列
在 0, 1, …, n - 1 这 n 个数字中,第一个被删除的数字是 (m - 1) % n。为了简单起见,我们把 (m - 1) % n 记为 k,那么删除 k 之后剩下的 n - 1 个数字为 0, 1, …, k - 1, k + 1, …, n - 1,并且下一次删除时要从 k + 1 开始计数。相当于在剩下的序列中, k + 1 排在最前面,所以第二次操作的序列是 k + 1, …, n - 1, 0, 1, …, k - 1。
- 得到新序列上函数
在这个新序列上再完成约瑟夫环操作,最后剩下的数字应该是关于 n 和 m 的函数,即也可以用 f(n, m) 进行表示。但由于现在的这个序列的排列(从 k + 1 开始)和最初的序列(从 0 开始)不一样,因此这个时候的函数已经不同于最初的函数,记为 h(n - 1, m),此函数的定义:在 k + 1, …, n - 1, 0, 1, …, k - 1 这 n - 1个数字的序列上做约瑟夫环操作,最后剩下的这个数字。
- 求解新函数
由于 在最初序列上 和 在新序列上 完成约瑟夫操作剩下的数字均为同一个数字,所以有 f(n, m) = h(n - 1, m)。(新序列是从最初序列转化的,会最终转化到同一个数字)
下面的工作就是求解新函数 h(n - 1, m) ,使其能够用 f(n - 1, m) 表示出来。
由于 f(n - 1, m) 是定义在以 0 为开始的序列上的,所以我们把剩下的这 n - 1 个数字的序列 k + 1, …, n - 1, 0, 1, …, k - 1 进行映射,映射到结果是形成一个 0 ~ n - 2 的序列。
k + 1 → 0
k + 2→ 1
…
n - 1 → n - k -2
0 → n - k - 1
1 → n - k
…
k - 1 → n - 2
该映射函数是个一元一次函数,定义为 p(x),则 p(x) = (x + n - k - 1) % n。(还记得初中的 y = x + a 怎么求么?如果不懂见附录1)
从左到右的映射是 p(x),从右到左的映射叫做逆映射 p-1(x) = (x + k + 1) % n。(该逆映射的求法见本章结尾附录2)
由于映射之后的序列和最初的序列有同样的形式,即都是从 0 开始的连续序列,因此在映射之后的序列上做约瑟夫环操作的结果仍可以用函数 f 表示,记为 f(n - 1, m)。
在映射之前的序列上的约瑟夫环操作的结果是 h(n - 1, m),在映射之后的序列上的约瑟夫环操作的结果是 f(n - 1, m),则 f(n - 1, m) = p( h(n - 1, m) )。
所以有:
h(n - 1, m) = p-1(x)( f(n - 1, m) ) = [ f(n - 1, m) + k + 1] % n
把 k = (m - 1) % n 代入得到:(k 中有取余运算,为什么代入之后没有了?见本章结尾附录3)
f(n, m) = h(n - 1, m) = [ f(n - 1, m) + m ] % n
终于,经过复杂的分析,我们找到了一个只包含有 f 函数的递推公式。要得到 n 个数字的序列中完成约瑟夫环操作最后剩下的数字,只需要得到 n - 1 个数字的序列中最后剩下的数字,并以此类推。(像不像递归?)
当 n = 1 时,也就是序列中只有 1 个数字 0,那么完成约瑟夫操作最后剩下的数字就是0。(像不像递归终止条件?)
我们把这种关系表示为:
f ( x ) = { 0 n = 1 [ f ( n − 1 , m ) + m ] % n n > 1 f(x)= \begin{cases} 0 & n = 1\\ \left[f(n - 1, m) + m\right]\% n & n>1 \end{cases} f(x)={0[f(n−1,m)+m]%nn=1n>1
这个公式无论是递归还是循环都很好实现。
附录0. 模运算的物理含义
附录1. p(x)的推导
看到这里的同学肯定好奇公式中的%号是怎么得到的,其实是个分段函数归纳的。
p ( x ) = { x − k − 1 k + 1 ≤ x ≤ n − 1 x + n − k − 1 0 ≤ x ≤ k − 1 p(x)= \begin{cases} x - k - 1 & k + 1 \leq x \leq n - 1\\ x + n - k - 1 & 0 \leq x \leq k - 1 \end{cases} p(x)={x−k−1x+n−k−1k+1≤x≤n−10≤x≤k−1
所以,为了把分段函数统一,使用 p(x) = (x + n - k - 1) % n。
附录2. p-1(x)的推导
已知p(x) = (x + n - k - 1) % n,求 p-1(x)。
p(x) = (x + n - k - 1) % n = (x + n - k - 1) + (T - 1)n = x - k - 1 + Tn
其中引入的正整数 T 的取值方法:取合适的 T 以保证0 <= p(x) <= n。(这一步不懂的可以用p(0) = n - k -1代入,此时 x = 0, T = 1)
可以得到x = p(x) + k + 1 - Tn,逆函数就是把 x 替换成 p(x),把 p(x) 替换成 x。
所以逆函数 p-1(x) = x + k + 1 - Tn = (x + k + 1) % n。
附录3. 消除括号里的模运算
模运算的四则规则:(a + b) % p = (a % p + b % p) % p,选自百度百科。
证明 [ f(n - 1, m) + (m - 1) % n + 1] % n = [ f(n - 1, m) + m ] % n .
左边 = [ f(n - 1, m) + (m - 1) % n + 1] % n
= [ (f(n - 1, m) + 1) % n + (m - 1) % n] % n ,由于0 < 映射后的取值 f(n - 1, m) < n - 2,所以1 < f(n - 1, m) + 1< n - 1,所以可以添加第一个取余运算。
= [ (f(n - 1, m) + 1) + (m - 1) ] % n ,运用四则运算公式
= [ f(n - 1, m) + m ] % n
= 右边
得证。
代码
pos = 0 开始,代表了最后结果只剩下了 1 个数字,这个数字处于第 0 个位置。
循环从数组长度有 2 个开始,即从剩下了两个数字开始计算。
循环到数组中剩下 n 个人结束,即到达了题目要求的那么多数字,此时的 pos 就是最后剩下的那个数字的在 n 个数字中位置。
Python 代码如下:
class Solution:
def lastRemaining(self, n: int, m: int) -> int:
pos = 0
for i in range(2, n + 1):
pos = (pos + m) % i
return pos
*注:本数学推导基于《剑指Offer》中的推导进行了更详细的讲解。
参考文献:
- 《剑指Offer》
- 力扣(LeetCode)链接:https://leetcode-cn.com/problems/yuan-quan-zhong-zui-hou-sheng-xia-de-shu-zi-lcof
- https://leetcode-cn.com/problems/yuan-quan-zhong-zui-hou-sheng-xia-de-shu-zi-lcof/solution/javajie-jue-yue-se-fu-huan-wen-ti-gao-su-ni-wei-sh/