编译原理中必不可少的算法：中缀表达式转后缀表达式

点赞再看，养成习惯！觉得不过瘾的童鞋，欢迎关注公众号《机器学习算法工程师》，有非常多大神的干货文章可供学习噢…

前言

这篇文章是对参考文献中NFA文章的补充，根据正规式构造NFA的步骤中有中缀表达式转后缀表达式的步骤，小编在这篇文章中将以耳熟能详的算式表达式（如：10+3-2*(5/1)）做例子，讲解中缀表达式转后缀表达式的原理。基本逻辑是：构造符号优先关系表、计算优先函数、中缀表达式转后缀表达式的流程。

正文

为简化模型，小编将字母d作为数字的抽象符号，还有用于指示表达式开始和结束的符号#，那么只包含简单的四则运算规则的算式表达式将包含的符号集为：$S=\{d,+,-,\ast ,/,(,),\#\}$。

构造符号优先关系表

构造符号优先关系表是属于语义分析的知识点，按理说是要先去了解算符优先分析法，不过在这里，小编更希望给童鞋们一个直观上的认识，就跳过概念直接给出了下面的优先关系表。小编从工程实践的角度来帮助大家认识这个优先关系表，首先我们需要知道isp和icp都是什么，前者指的是在栈顶的符号优先级，后者指的是从输入的中缀表达式中读取到的当前符号优先级。然后，我们需要知道在表格中那些{>,<,空}都意味着什么，{>,<}就是我们了解到的大于小于，而空则表示这种情况在中缀表达式构造正确的情况下不会出现isp的那个栈顶元素与icp当前元素相遇的情况，可以举个例子，如果中缀表达式为d+d(d+d)这种情况，d(d就是不正确的构造，中间缺少运算符。最后，我们需要知道这些关系是如何得来的，这其实就是人为设定的规则，具体有：

• 先括号内，再括号外；
• 乘法除法优先级高于加法减法；
• 同优先级情况下，自左向右；
• 开始结束符号#优先级最低，数字d优先级最高，互相匹配的符号优先级相同。

isp\icp	+	-	*	/	(	)	#	d
+	>	>	<	<	<	>	>	<
-	>	>	<	<	<	>	>	<
*	>	>	>	>	<	>	>	<
/	>	>	>	>	<	>	>	<
(	<	<	<	<	<	=		<
)	>	>	>	>		>	>
#	<	<	<	<	<		=	<
d	>	>	>	>		>	>

对这个优先关系表构造有兴趣的童鞋，小编建议去看看参考文献中那本书籍，这个知识点以及下面计算优先函数的知识点都在第6章自底向上优先分析中。

计算优先函数

其实有了上面一节的优先关系表，我们就可以直接开始中缀表达式转后缀表达式的流程，怎么做呢？最简单的就是使用一个哈希结构，key便是一个元组(c1,c2)，c1表示当前栈顶符号，c2表示当前读取的符号，取出value，便是优先级(0代表相同，1表示c1优先级大于c2，-1表示c1优先级小于c2，-2表示空，程序应该中止报错)。但为什么还要有这一计算优先函数的一步呢？优先函数是什么呢？这完全是从节省存储空间的角度出发想出的替代方法，原先优先关系表会占用nxn个内存单元，n表示符号集元素个数，但是如果能够转化为优先函数（即isp和icp函数，输入为符号ch，输出为该符号ch的优先级数值），那么只需2n个单元，将大大节省存储空间。
那么优先关系表如何得到优先函数呢？这其实也有严格的理论，不过小编这里还是直接给出最终的结果，鼓励童鞋们自行探索。

	+	-	*	/	(	)	#	d
isp	3	3	5	5	1	5	1	5
icp	2	2	4	4	6	1	1	6

下面是小编编写的转化代码，供童鞋们参考：

"""
@description:
根据优先关系表计算优先函数
@author: 一帆
@date: 2020/6/10
"""

def getPriorityFunc(pt,n):
    # 初始化isp/icp
    pfunc = [[1]*n for _ in range(2)]
    # 迭代，直至flag不再变动或者超过限制的迭代轮数
    flag = False
    iter = 1
    limit_iter = 10
    while not flag and iter<=limit_iter:
        print("迭代轮数：",iter)
        iter+=1
        for a in range(n):
            for b in range(n):
                if pt[a][b]==1 and pfunc[0][a]<=pfunc[1][b]:
                    #isp(a)优先级高于icp(b)且isp(a)<=icp(b)，则isp(a)=icp(b)+1
                    pfunc[0][a]=pfunc[1][b]+1
                    flag=True
                elif pt[a][b]==-1 and pfunc[0][a]>=pfunc[1][b]:
                    pfunc[1][b]=pfunc[0][a]+1
                    flag=True
                elif pt[a][b]==0 and pfunc[0][a]!=pfunc[1][b]:
                    if pfunc[0][a]<pfunc[1][b]:
                        pfunc[0][a]=pfunc[1][b]
                    else:
                        pfunc[1][b]=pfunc[0][a]
                    flag=True
        if not flag:
            return pfunc
        else:
            flag=False
    return None


if __name__ == '__main__':
    pt = [[1,1,-1,-1,-1,1,1,-1],
          [1,1,-1,-1,-1,1,1,-1],
          [1,1,1,1,-1,1,1,-1],
          [1,1,1,1,-1,1,1,-1],
          [-1,-1,-1,-1,-1,0,-2,-1],
          [1,1,1,1,-2,1,1,-2],
          [-1,-1,-1,-1,-1,-2,0,-1],
          [1,1,1,1,-2,1,1,-2]]
    pfunc = getPriorityFunc(pt,len(pt))
    print(pfunc)

中缀表达式转后缀表达式

经过了前面的准备工作，有了isp和icp这两个优先函数，我们终于可以着手开始中缀表达式向后缀表达式的转化了。基本逻辑如下图所示：

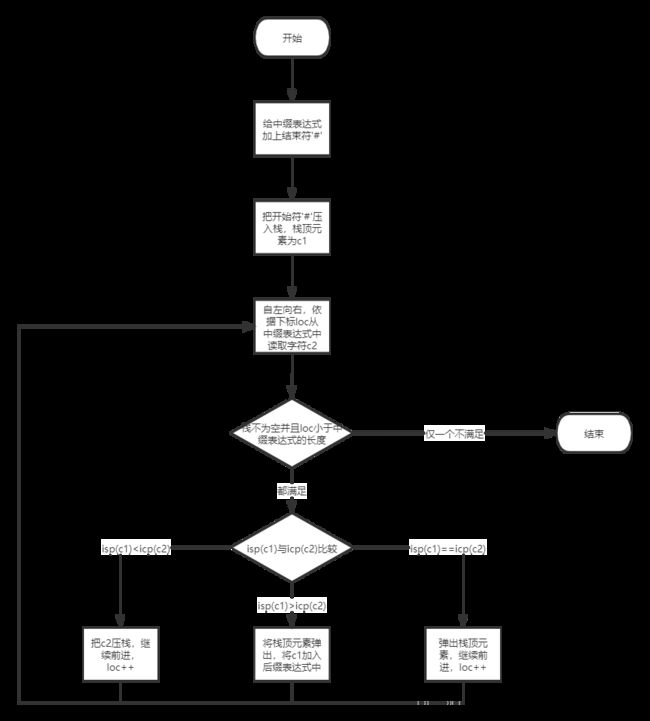
对应的代码如下：

"""
@description:
实现中缀表达式向后缀表达式地转化
符号集：数字[d]、四则运算[+-*/]和括号[()]
@author: 一帆
@date: 2020/6/10
"""

import sys


class In2Postfix:
    def __init__(self, infix_expression):
        self.__infix = infix_expression
        self.__postfix = ""
        self.__isp = {'+': 3, '-': 3, '*': 5, '/': 5, '(': 1, ')': 5, '#': 1, 'd': 5}
        self.__icp = {'+': 2, '-': 2, '*': 4, '/': 4, '(': 6, ')': 1, '#': 1, 'd': 6}

    def ispFunc(self, char):
        priority = self.__isp.get(char, -1)
        if priority == -1:
            print("error: 出现未知符号！")
            sys.exit(1)  # 异常退出
        return priority

    def icpFunc(self, char):
        priority = self.__icp.get(char, -1)
        if priority == -1:
            print("error: 出现未知符号！")
            sys.exit(1)  # 异常退出
        return priority

    def in2post(self):
        infix = self.__infix + '#'
        stack = ['#']
        loc = 0
        while stack and loc < len(infix):
            c1, c2 = stack[-1], infix[loc]
            if self.ispFunc(c1) < self.icpFunc(c2):
                # 栈外字符优先级更高，压栈
                stack.append(c2)
                loc += 1  # 前进
            elif self.ispFunc(c1) > self.icpFunc(c2):
                # 栈顶字符优先级更高，弹出
                self.__postfix += stack.pop()
            else:
                # 优先级相等，要么结束了，要么碰到右括号了，都弹出但并不添加至后缀表达式中
                stack.pop()
                loc += 1

    def getResult(self):
        self.in2post()
        return self.__postfix


if __name__ == '__main__':
    infix_expression = "d+d-d*(d/d)"  # 简单测试
    # infix_expression = input("请输入算式表达式：")
    print("infix_expression:", infix_expression)
    solution = In2Postfix(infix_expression)
    print("postfix_expression:", solution.getResult())

结语

其实小编还是有点疑惑的，根据正规式构造NFA是词法分析的知识点，但是其构造过程却涉及到本篇文章讲述的算法，而这个算法是在后面语义分析才会学到的，所以小编想这应该是为什么有那么多童鞋找小编要NFA的源码的原因吧。本篇中的重难点知识点集中在符号优先级关系的确定与优先函数的计算，理论性非常强，但编程实现却并不难，建议正在学习编译原理的童鞋尽量自行实现，实在卡住了再来参考借鉴。

参考文献

1. 张素琴. 《编译原理》第二版
2. NFA: https://blog.csdn.net/gongsai20141004277/article/details/52949995

童鞋们，让小编听见你们的声音，点赞评论，一起加油。