NLP基础(二):递归神经网络
1.RNN
RNN神经网络每一个状态的输出与上一个状态的输出有关, x t x_t xt和 h t − 1 h_{t-1} ht−1进行拼接作为神经网络的输入计算得到 t t t时刻的输出 h t h_t ht, h 1 = f ( h 0 , x 0 ) h_1=f(h_0, x_0) h1=f(h0,x0)。因此RNN模型无法进行GPU并行加速。
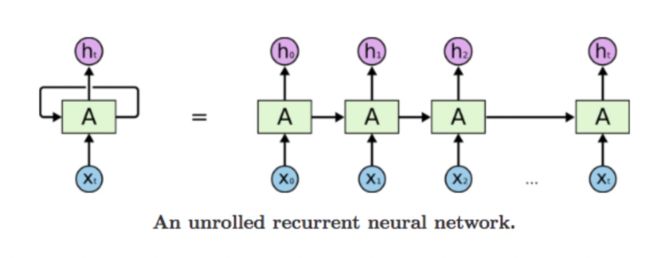
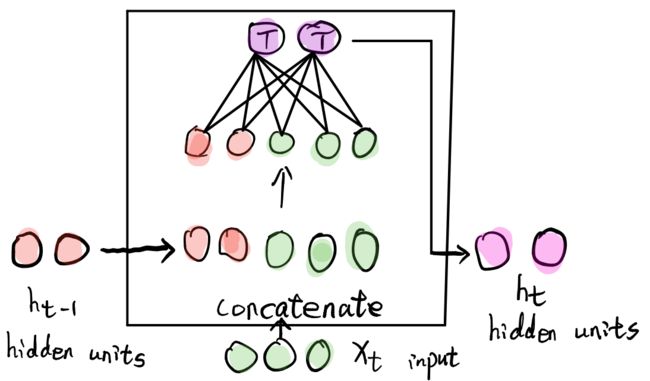
1.1 parameter sharing
神经网络的参数为 w h w_h wh,通过不断循环递归训练得到该参数。
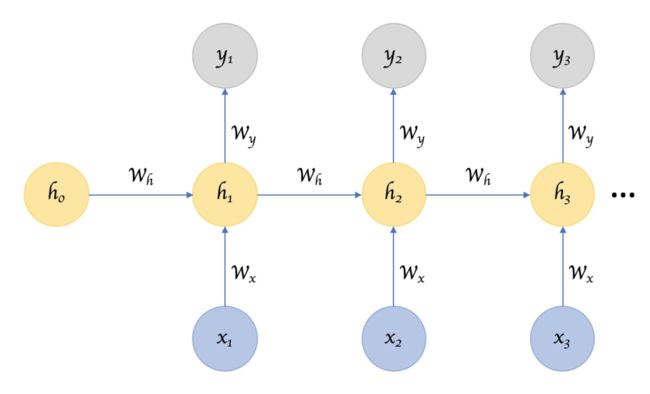
1.2 Exploding and Vanishing
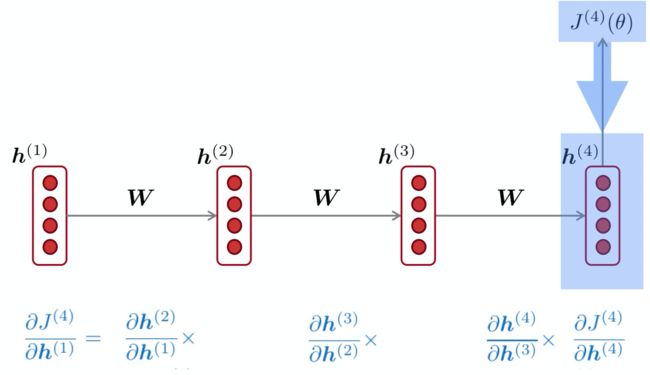
根据链式法则,在导数值很小的情况下,经过连乘,出现梯度消失的现象。由于RNN常采用sigmoid激活函数 σ ( w x + b ) \sigma(wx+b) σ(wx+b),在 w x + b wx+b wx+b很小或很大时,其导数会非常小,比如0.0001,在反向传播时出现梯度消失。
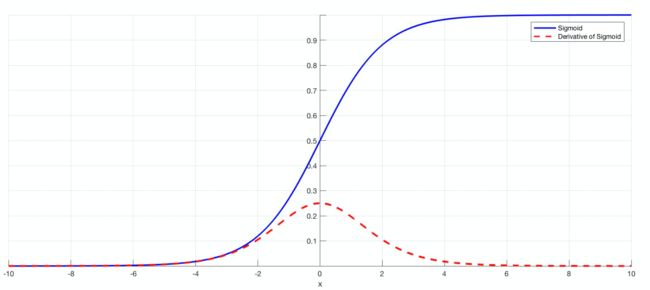
1)解决梯度爆炸的方法:截断
在梯度值达到阈值时,取阈值,直接截断。 i f ∣ ∣ g ∣ ∣ > t h r e s h o l d , g = t h r e s h o l d × g ∣ ∣ g ∣ ∣ if ||g||>threshold,g=\frac {threshold \times g}{||g||} if∣∣g∣∣>threshold,g=∣∣g∣∣threshold×g。
2)解决梯度消失的方法
A.更换激活函数:tanh,relu
B.更换结构:LSTM,GRU
C.ResNet残差网络
何恺明大佬提出的残差网络,通过残差的连接跳过导数的连乘,有效解决deep神经网络层数过深导致梯度消失的问题。
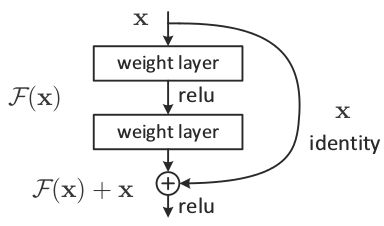
D.Batch Normalization
在样本内进行归一化(均值为0,方差为1),保证x在绿色的合理范围内,防止经过sigmoid函数出现导数过小的情况出现。
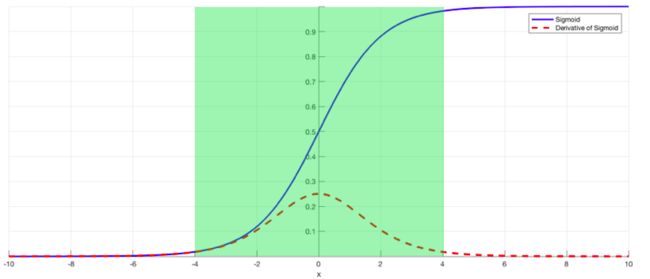
2.LSTM
LSTM由遗忘门、输入门、输出门三个门组成。
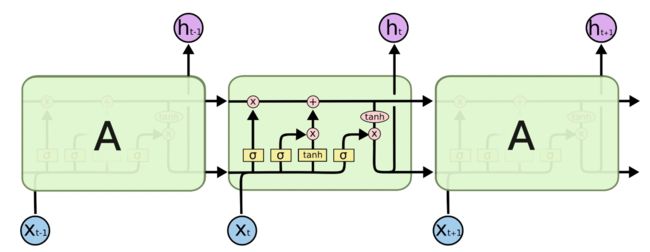
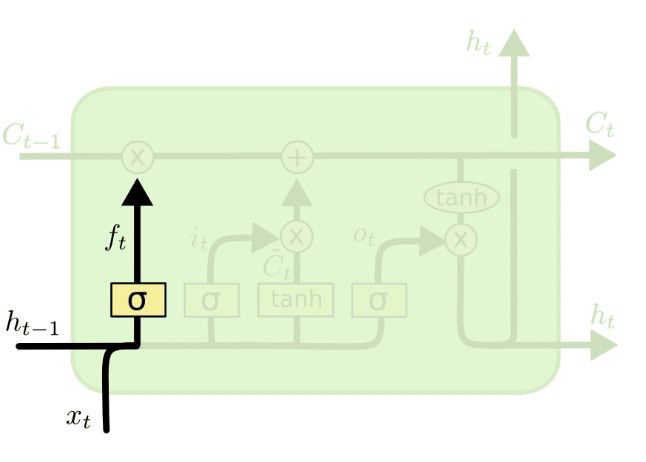
1)forget gate: f t = σ ( w f [ h t − 1 , x t ] + b f ) f_t = \sigma(w_f[h_{t-1},x_t]+b_f) ft=σ(wf[ht−1,xt]+bf)
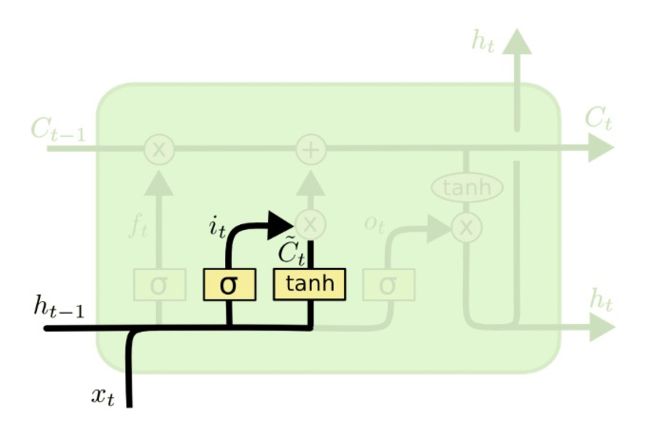
2)input gate: i t = σ ( w i [ h t − 1 , x t ] + b i ) , C ~ t = t a n h ( w c [ h t − 1 , x t ] + b c ) i_t = \sigma(w_i[h_{t-1},x_t]+b_i),\widetilde C_t=tanh(w_c[h_{t-1},x_t]+b_c) it=σ(wi[ht−1,xt]+bi),C t=tanh(wc[ht−1,xt]+bc)
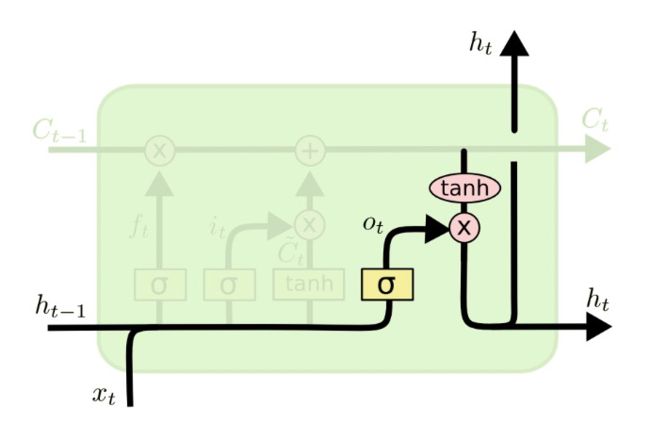
3)output gate: o t = σ ( w o [ h t − 1 , x t ] + b o ) o_t = \sigma(w_o[h_{t-1},x_t]+b_o) ot=σ(wo[ht−1,xt]+bo)
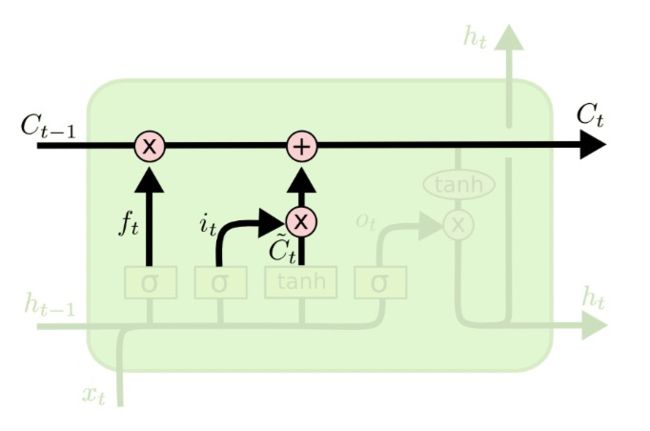
4)长记忆: C t = f t ∗ C t − 1 + i t ∗ C ~ t C_t = f_t \ast C_{t-1}+i_t \ast \widetilde C_t Ct=ft∗Ct−1+it∗C t
4)短记忆: h t = o t ∗ t a n h ( C t ) h_t=o_t \ast tanh(C_t) ht=ot∗tanh(Ct)
3.GRU
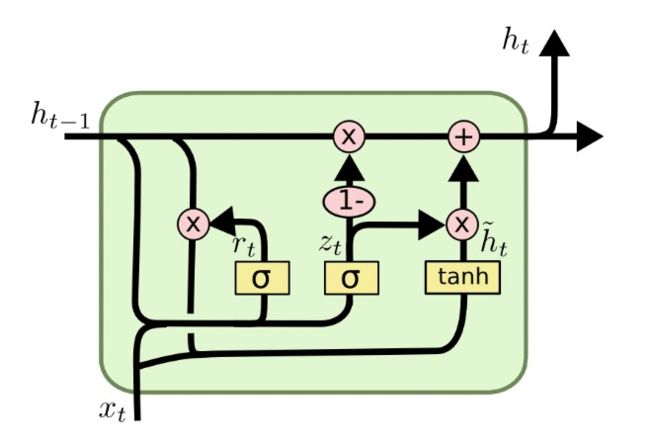
与LSTM不同,GRU只有两个门了,分别为重置门和更新门。GRU较LSTM所需数据集较少一些,速度也更快一些。
1)重置门: r t = σ ( w r [ h t − 1 , x t ] + b r ) r_t = \sigma(w_r[h_{t-1},x_t]+b_r) rt=σ(wr[ht−1,xt]+br)
2)更新门: z t = σ ( w z [ h t − 1 , x t ] + b z ) z_t = \sigma(w_z[h_{t-1},x_t]+b_z) zt=σ(wz[ht−1,xt]+bz)
3)记忆: h ~ t = t a n h ( r t ∗ h t − 1 , x t ) , h t = ( 1 − z t ) ∗ h t − 1 + z t ∗ h ~ t \widetilde h_t =tanh(r_t \ast h_{t-1}, x_t),h_t=(1-z_t) \ast h_{t-1}+z_t \ast \widetilde h_t h t=tanh(rt∗ht−1,xt),ht=(1−zt)∗ht−1+zt∗h t
参考文献
[1]word2vec Parameter Learning Explained
[2]LSTM原理及实现(一)