线段树入门+例题
线段树入门
最近预备队里教了线段树,刚学的时候只是觉得神奇,但是还是有点迷,后来自己对这个数据结构进行了琢磨,发现真的是非常的巧妙。正好趁热打铁,对线段树总结一下。
为什么需要线段树?
假设我们有一个数组arr,对于这个数组,我们有两种操作,第一种操作就是求从arr数组从某一区间的和,第二种操作就是修改arr中的某一个值或者是修改某一区间的值。
针对此问题,我们最简单的有两种方法。
**第一种:**对于修改操作,我们可以直接改变该位置的值,这种时间复杂度为o(1),但是对于求和,我们需要arr[i]+arr[i+1]+……+arr[j],而这样的时间复杂度为o(n);
**第二种:**对于求和操作,我们可以事先创建一个数组sum用来保存前缀和,那么从i到j求和,只需要sum[j]-sum[i-1]即可,这样的时间复杂度为o(1),但是对于修改操作,我们修改了arr数组中的值,需要将前缀和数组sum也给修改一遍,这样的时间复杂度就为o(n)了;
由上可知,当数据足够大、操作足够多的时候,以上两种两种方法都在某一操作的时候会有十分大的复杂度,这是我们不能接受的,所以为了取一个折中的方案,我们就引入了线段树这一数据结构。因为是二分思想,所以对于修改和求和,线段树的时间复杂度都是o(logn)。
什么是线段树?
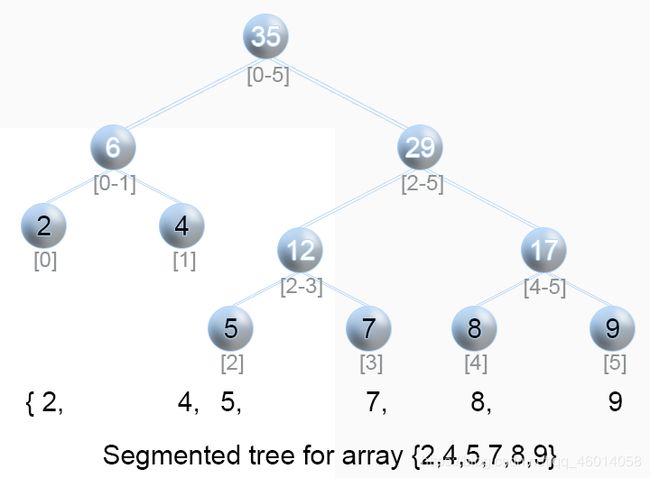
1、线段树,顾名思义,他就是树,线段树的实质就是一棵二叉搜索树,它的每个节点都存放着数组某一区间的和,而不仅仅是某一位置的值。
我们可以看到,每个叶节点都是存放着数组某一位置的值,而其他节点的值,则是它的两个儿子的值的和。
3、线段树的特殊性质:
(1)线段树中的一个节点的范围是从start到end,那么其左儿子的范围是便是从start到mid,右儿子的范围是从mid+1到end。
(2)线段树的第node个结点,它的左儿子是线段树中的第node*2个节点,而右儿子是线段树中的第(node*2+1)个节点。
4、实现线段树的重要思想——二分法!
怎么使用线段树?
要想实现线段树的功能,主要四种操作:建立线段树、单点修改、区间修改、区间查询
1、建立线段树
代码:
void build_tree(int arr[],int tree[],int node,int start,int end)
{
if(start==end)
tree[node]=arr[start];
else
{
int mid = (start+end)/2;
int left_node=2*node;
int right_node=2*node+1;
build_tree(arr,tree,left_node,start,mid);
build_tree(arr,tree,right_node,mid+1,end);
tree[node]=tree[left_node]+tree[right_node];
}
}
我们这里是已经有了一个arr数组,我们将这个数组建成一棵树。这个函数的目的就是以当前的node结点建树,并且求出tree[node]这个位置的值。
先看这个函数的形参。arr[]表示现有的数组,tree[]表示存储这棵树的数组,node表示当前结点,而start和end表示这个结点控制的范围。
如果start==end,那么就限制说明线段树中的这个结点只负责arr数组中的这一个结点,也就是说明这是一个叶节点,不能继续往下建树了,那么就将这个tree[node]赋上arr[start]的值(此时start和end都是一样的,都是同一个点,那这里用start还是用end都是一样的)。
如果start!=end,说明当前结点负责的还是一个区间,只要是个区间,他就可以继续往下分。我们要想求tree[node]的值,就必须先求出来node两个儿子的值,然后再加起来,而想要求他的两个儿子的值,就需要递归调用build函数。那这里调用build函数的时候,参数怎么填呢?我们说过,线段树的一个重要思维就是二分法,我们需要将这个区间均分成两半,一段是[start,mid],另一端就是[mid+1,end],而node结点的左子节点是node*2,右子节点是node*2+1,所以我们分别以左子节点和左半区域、右子节点和右半区域为参量调用build函数,再把这两个子节点的值加起来,就求出了tree[node]的值。
这样只要一直递归下去,就能建成一棵线段树。
2、单点修改
代码:
void update_point(int arr[],int tree[],int node,int start,int end,int idx,int val)
{
if(start==end)
{
arr[idx]=val;
tree[node]=val;
}
else
{
int mid = (start+end)/2;
int left_node=2*node;
int right_node=2*node+1;
if(idx>=start &&idx<=mid)
update_tree(arr,tree,left_node,start,mid,idx,val);
else
update_tree(arr,tree,right_node,mid+1,end,idx,val);
tree[node]=tree[left_node]+tree[right_node];
}
}
这个函数的功能就是单点修改,将arr数组的第pos个元素修改为val,并且维护好这个线段树。
这里主要是使用了二分查找,递归查找到arr[pos]在tree中的位置,修改这个值,并在每次递归过后,维护一下父节点的值。因为修改单个结点,只会影响到查找过程中经历过的结点,所以仅需每次维护父节点,就能保证整棵树没有问题。
3、区间修改
为了减少额外操作,我们这里引入一个新的标签——lazy tag(懒标签)。为什么叫做懒标签呢,因为他就是懒得动,让他移动一下就跟挤牙膏一样,按理说他应该把下面所有的结点都更新,但是他就只下放一次,你说这懒不懒。但是懒也有懒的好处,那就是操作少了,时间也少了,你不查询这个结点,那我就不进行额外的操作,能够省下好多时间。
当我们对线段树进行更新或者查询的时候,如果当前节点有lazy tag的标记,那我们就下放(pushdown)一次,并且将树中该节点的子节点的值加上lazy tag标记的值乘上这个子结点负责的区域的长度,那么这就相当于把更新这段区间内的所有点所需要的值都加上了。
那我们什么时候需要标记lazy tag呢?当我们在递归过程中,发现当前结点负责的区间,是包含在所要修改的区间内的,那么我们就没有必要继续向下递归,直接打上标记即可。
void pushdown(int tree[], int node, int length)
{
if (tag[node])
{
int c = tag[node];
tag[node] = 0;
int left_node = node << 1,right_node = node << 1 | 1;
tag[left_node] = c,tag[right_node] = c;
tree[left_node] = c * (length - (length >> 1));
tree[right_node] = c * (length >> 1);
}
}
void update_segment(int arr[],int tree[],int node, int start, int end, int L, int R, int val)
{
if (L <= start && end <= R)
{
tag[node] = val;
tree[node] = val * (end - start + 1);
return;
}
pushdown(tree, node, end - start + 1);
int mid = (start + end) / 2;
int left_node = node * 2;
int right_node = node * 2 + 1;
if (L <= mid)
update(arr, tree, left_node, start, mid, L, R, val);
if (R > mid)
update(arr, tree, right_node, mid + 1, end, L, R, val);
tree[node] = tree[left_node] + tree[right_node];
}
我们这里进行递归,只有当当前结点负责的区间被包含于修改区间的时候才会打上标记,否则调用这个函数的时候回一直向下递归,一直递归到叶节点,进而保证这个区间的准确性(有大区间就将这个大区间标记上,如果一直没有大区间,那就将最底下的叶节点修改,最后将叶节点的区间和大区间加起来就是目标结点了)。
4、区间查询
代码
int query_tree(int arr[],int tree[],int node,int start,int end,int L,int R)
{
if(start>R||end对于区间查询,目标区间和当前区间之间有这么几种关系:
1、
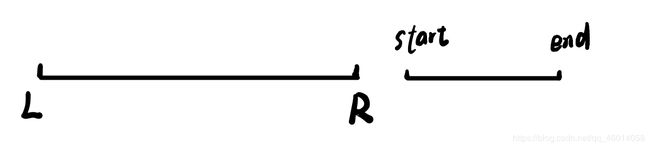
当前区间与目标区间无交集,那么不用往下继续找,这段区间的和肯定为0,所以直接return 0就好。
当前区间被包含于目标区间,那么这段区间的所有值都要了,直接return tree[node]即可。
3、
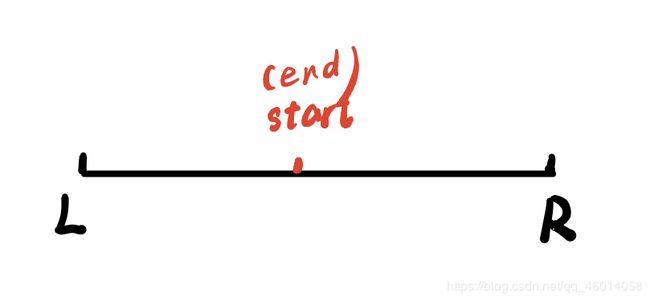
当前start==end,说明这已经找到了叶节点,而这叶节点也在目标区间内,那么也没办法往下找,return tree[node]即可。
4、
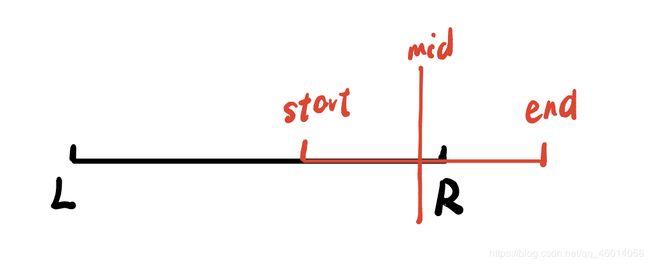
此时当前区间与目标区间有交集,那此时怎么求呢?我们可以递归求出左半区间在目标区间中的和以及右半区间在目标区间中的和,将这两个和相加,就得到了总区间的和。这里是递归思想,最终会求到最小的满足条件的区间的和。
例题
1、[HDU 1166] 敌兵布阵
这道题目就是线段树单点修改区间查询的模板题,套模板即可。注意在update的时候,不是将arr[pos]修改为val,而是加上val。
AC代码
#include
#include
#include
using namespace std;
int arr[50005];
int tree[200010];
void build(int node, int start, int end)
{
if (start == end)
tree[node] = arr[end];
else
{
int mid = (start + end)>>1;
int left_node = node <<1;
int right_node = (node <<1) + 1;
build(left_node, start, mid);
build(right_node, mid + 1, end);
tree[node] = tree[left_node] + tree[right_node];
}
}
void update(int node, int start, int end, int pos, int val)
{
if (start == end)
{
arr[pos] += val;
tree[node] += val;
}
else {
int mid = (start + end) >> 1;
int left_node = node << 1;
int right_node = (node << 1) + 1;
if (pos >= start && pos <= mid)
update(left_node, start, mid, pos, val);
else
update(right_node, mid + 1, end, pos, val);
tree[node] = tree[left_node] + tree[right_node];
}
}
int query(int node, int start, int end, int L, int R)
{
if (L > end || R < start)
return 0;
else if (start == end)
return tree[node];
else if (start >= L && R >= end)
return tree[node];
else
{
int mid = (start + end) >> 1;
int left_node = node << 1;
int right_node = (node << 1) + 1;
int sum_left = query(left_node, start, mid, L, R);
int sum_right = query(right_node, mid + 1, end, L, R);
return sum_left + sum_right;
}
}
int main(void)
{
int T;
cin >> T;
for (int i = 1; i <= T; i++)
{
int n;
cin >> n;
for (int j = 1; j <= n; j++)
scanf("%d", arr + j);
build(1, 1, n);
string op;
printf("Case %d:\n", i);
while (cin >> op)
{
if (op == "End")break;
else if (op == "Query")
{
int start, end;
cin >> start >> end;
int ans = query(1, 1, n, start, end);
cout << ans << endl;
}
else if (op == "Add")
{
int pos, val;
cin >> pos >> val;
update(1, 1, n, pos, val);
}
else if (op == "Sub")
{
int pos, val;
cin >> pos >> val;
update(1, 1, n, pos, -val);
}
}
}
return 0;
}
2、[HDU 1698]Just a Hook
线段树区间修改的模板题,在建树的时候,我们直接将叶节点的值设置为1即可,就不用额外的arr数组了,另外将tree和tag设置为全局变量也更加方便。最后要求和,直接输出线段树的第一个结点即可。
AC代码
#include
using namespace std;
const int maxn = 400010;
int tree[maxn];
int tag[maxn];
void build(int node, int start, int end)
{
tag[node] = 0;
if (start == end)
tree[node] = 1;
else
{
int mid = (start + end) >> 1;
int left_node = node << 1;
int right_node = (node << 1) | 1;
build(left_node, start, mid);
build(right_node, mid + 1, end);
tree[node] = tree[left_node] + tree[right_node];
}
}
void pushdown(int node, int length)
{
if (tag[node])
{
int c = tag[node];
tag[node] = 0;
int left_node = node << 1;
int right_node = node << 1 | 1;
tag[left_node] = c;
tag[right_node] = c;
tree[left_node] = c * (length - (length >> 1));
tree[right_node] = c * (length >> 1);
}
}
void update(int node, int start, int end, int L, int R, int val)
{
if (L <= start && end <= R)
{
tag[node] = val;
tree[node] = val * (end - start + 1);
return;
}
pushdown(node, end - start + 1);
int mid = (start + end) >> 1;
int left_node = node << 1;
int right_node = node << 1 | 1;
if (L <= mid)
update(left_node, start, mid, L, R, val);
if (R > mid)
update(right_node, mid + 1, end, L, R, val);
tree[node] = tree[left_node] + tree[right_node];
}
int main(void)
{
ios::sync_with_stdio(false);
int T;
cin >> T;
for (int i = 1; i <= T; i++)
{
int n;
cin >> n;
build(1, 1, n);
int op;
cin >> op;
for (int j = 0; j < op; j++)
{
int l, r, val;
cin >> l >> r >> val;
update(1, 1, n, l, r, val);
}
printf("Case %d: The total value of the hook is %d.\n", i, tree[1]);
}
return 0;
}
我自己也是刚刚学习这部分,虽然说写出来之后受益匪浅,但终究还是理解有限,未来还需要多多刷题以增加熟练度。如果这篇文章有问题,希望有大佬能够批评指正,谢谢各位。