机器学习笔记（五） 机器学习（特征工程）

主要来源：视频学习网站Google机器学习教程

将原始数据映射到特征

传统编程的特征点是代码，而在机器学习项目中，关注点就是特征表示。也就是说，开发者通过添加或改善特征来调整模型；

特征工程：指的是将原始数据转换为特征矢量。（往往特征工程会占用整个工作的大部分时间精力）
许多机器学习模型都必须将特征表示为实数向量，因为特征值必须与模型权重相乘。
下图左侧表示来自输入数据源的原始数据，右侧表示特征矢量，也就是组成数据集中样本的浮点值集。

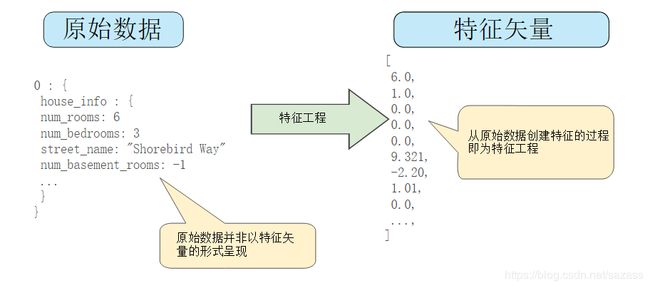
映射数值
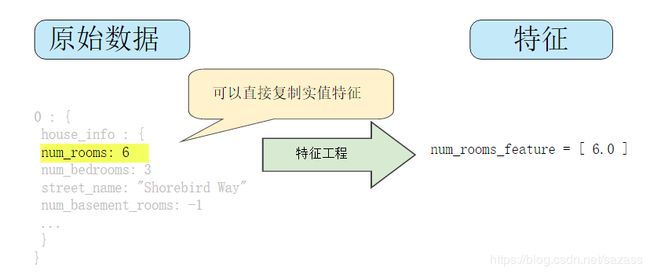
整数和浮点数据不需要特殊编码，因为它们可以与数字权重相乘。如下图所示，将原始整数值 6 转换为特征值 6.0 并没有多大的意义：

映射分类值
分类特征具有一组离散的可能值。例如，可能有一个名为 street_name 的特征，其中的选项包括：
{‘Charleston Road’, ‘North Shoreline Boulevard’, ‘Shorebird Way’, ‘Rengstorff Avenue’}
由于模型不能将字符串与学习到的权重相乘，因此我们使用特征工程将字符串转换为数字值。

要实现这一点，我们可以定义一个从特征值（我们将其称为可能值的词汇表）到整数的映射。世界上的每条街道并非都会出现在我们的数据集中，因此我们可以将所有其他街道分组为一个全部包罗的“其他”类别，称为 OOV（词汇表外）分桶。

通过这种方法，我们可以按照以下方式将街道名称映射到数字：

将 Charleston Road 映射到 0
将 North Shoreline Boulevard 映射到 1
将 Shorebird Way 映射到 2
将 Rengstorff Avenue 映射到 3
将所有其他街道 (OOV) 映射到 4

不过，如果我们将这些索引数字直接纳入到模型中，将会造成一些可能存在问题的限制：

我们将学习适用于所有街道的单一权重。例如，如果我们学习到 street_name 的权重为 6，那么对于 Charleston Road，我们会将其乘以 0，对于 North Shoreline Boulevard 则乘以 1，对于 Shorebird Way 则乘以 2，依此类推。以某个使用 street_name 作为特征来预测房价的模型为例。根据街道名称对房价进行线性调整的可能性不大，此外，这会假设您已根据平均房价对街道排序。我们的模型需要灵活地为每条街道学习不同的权重，这些权重将添加到利用其他特征估算的房价中。
我们没有将 street_name 可能有多个值的情况考虑在内。例如，许多房屋位于两条街道的拐角处，因此如果模型包含单个索引，则无法在 street_name 值中对该信息进行编码。

要去除这两个限制，我们可以为模型中的每个分类特征创建一个二元向量来表示这些值，如下所述：
对于适用于样本的值，将相应向量元素设为 1；
将所有其他元素设为 0；
该向量的长度等于词汇表中的元素数。当只有一个值为 1 时，这种表示法称为独热编码；当有多个值为 1 时，这种表示法称为多热编码。
下图所示为街道 Shorebird Way 的独热编码。在此二元矢量中，代表 Shorebird Way 的元素的值为 1，而代表所有其他街道的元素的值为 0。

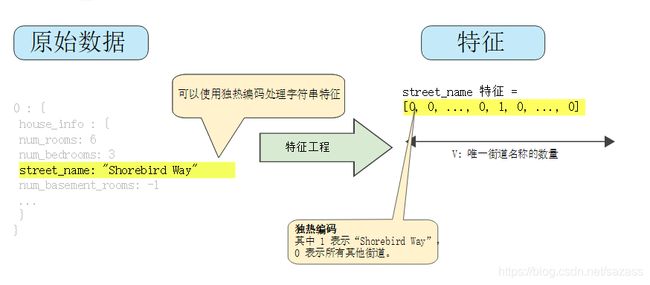
该方法能够有效地为每个特征值（例如，街道名称）创建布尔变量。采用这种方法时，如果房屋位于 Shorebird Way 街道上，则只有 Shorebird Way 的二元值为 1。因此，该模型仅使用 Shorebird Way 的权重。

同样，如果房屋位于两条街道的拐角处，则将两个二元值设为 1，并且模型将使用它们各自的权重。
独热编码会扩展到您不希望直接与权重相乘的数字数据，例如邮政编码。

稀疏表示法 (sparse representation)
假设数据集中有 100 万个不同的街道名称，您希望将其包含为 street_name 的值。如果直接创建一个包含 100 万个元素的二元向量，其中只有 1 或 2 个元素为 ture，则是一种非常低效的表示法，在处理这些向量时会占用大量的存储空间并耗费很长的计算时间。在这种情况下，一种常用的方法是使用稀疏表示法，其中仅存储非零值。在稀疏表示法中，仍然为每个特征值学习独立的模型权重，如上所述。

例如，假设以两种方式来表示句子“Dogs wag tails.”。如下表所示，密集表示法将使用约一百万个单元格；稀疏表示法则只使用 3 个单元格：

良好特征的特点

1.避免很少使用的离散特征值
良好的特征值应该在数据集中出现大约 5 次以上。这样一来，模型就可以学习该特征值与标签是如何关联的。也就是说，大量离散值相同的样本可让模型有机会了解不同设置中的特征，从而判断何时可以对标签很好地做出预测。例如，house_type 特征可能包含大量样本，其中它的值为 victorian：

相反，如果某个特征的值仅出现一次或者很少出现，则模型就无法根据该特征进行预测。例如，unique_house_id 就不适合作为特征，因为每个值只使用一次，模型无法从中学习任何规律：

2.最好具有清晰明确的含义
每个特征对于项目中的任何人来说都应该具有清晰明确的含义。例如，下面的房龄适合作为特征，可立即识别是以年为单位的房龄：

相反，对于下方特征值的含义，除了创建它的工程师，其他人恐怕辨识不出：

在某些情况下，混乱的数据（而不是糟糕的工程选择）会导致含义不清晰的值。例如，以下 user_age 的来源没有检查值恰当与否：

3.实际数据内不要掺入特殊值
良好的浮点特征不包含超出范围的异常断点或特殊的值。例如，假设一个特征具有 0 到 1 之间的浮点值。那么，如下值是可以接受的：

不过，如果用户没有输入 quality_rating，则数据集可能使用如下特殊值来表示不存在该值：

为解决特殊值的问题，需将该特征转换为两个特征：

一个特征只存储质量评分，不含特殊值。
一个特征存储布尔值，表示是否提供了 quality_rating。为该布尔值特征指定一个名称，例如 is_quality_rating_defined。

4.考虑上游不稳定性
特征的定义不应随时间发生变化。例如，下列值是有用的，因为城市名称一般不会改变。（注意，我们仍然需要将“br/sao_paulo”这样的字符串转换为独热矢量。）

但收集由其他模型推理的值会产生额外成本。可能值“219”目前代表圣保罗，但这种表示在未来运行其他模型时可能轻易发生变化：

清理数据

作为一名机器学习工程师，您将花费大量的时间挑出坏样本并加工可以挽救的样本。即使是非常少量的“坏苹果”也会破坏掉一个大规模数据集。

缩放特征值

缩放是指将浮点特征值从自然范围（例如 100 到 900）转换为标准范围（例如 0 到 1 或 -1 到 +1）。如果某个特征集只包含一个特征，则缩放可以提供的实际好处微乎其微或根本没有。不过，如果特征集包含多个特征，则缩放特征可以带来以下优势：

1.帮助梯度下降法更快速地收敛。
2.帮助避免“NaN 陷阱”。在这种陷阱中，模型中的一个数值变成 NaN（例如，当某个值在训练期间超出浮点精确率限制时），并且模型中的所有其他数值最终也会因数学运算而变成 NaN。
3.帮助模型为每个特征确定合适的权重。如果没有进行特征缩放，则模型会对范围较大的特征投入过多精力。
您不需要对每个浮点特征进行完全相同的缩放。即使特征 A 的范围是 -1 到 +1，同时特征 B 的范围是 -3 到 +3，也不会产生什么恶劣的影响。不过，如果特征 B 的范围是 5000 到 100000，您的模型会出现糟糕的响应。

处理极端离群值
下面的曲线图表示的是加利福尼亚州住房数据集中称为 roomsPerPerson 的特征。roomsPerPerson 值的计算方法是相应地区的房间总数除以相应地区的人口总数。该曲线图显示，在加利福尼亚州的绝大部分地区，人均房间数为 1 到 2 间。不过，请看一下 x 轴：

如何最大限度降低这些极端离群值的影响？一种方法是对每个值取对数

对数缩放可稍稍缓解这种影响，但仍然存在离群值这个大尾巴。我们来采用另一种方法。如果我们只是简单地将 roomsPerPerson 的最大值“限制”为某个任意值（比如 4.0），会发生什么情况呢？

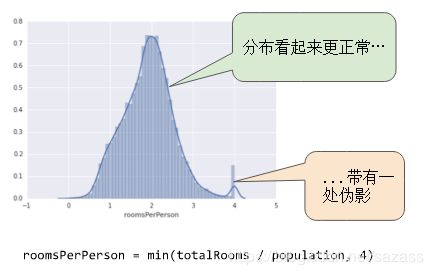
将特征值限制到 4.0 并不意味着我们会忽略所有大于 4.0 的值。而是说，所有大于 4.0 的值都将变成 4.0。这就解释了 4.0 处的那个有趣的小峰值。尽管存在这个小峰值，但是缩放后的特征集现在依然比原始数据有用。

分箱（应用于特征与标签没有线性关系模型中）
下面的曲线图显示了加利福尼亚州不同纬度的房屋相对普及率。注意集群 - 洛杉矶大致在纬度 34 处，旧金山大致在纬度 38 处。

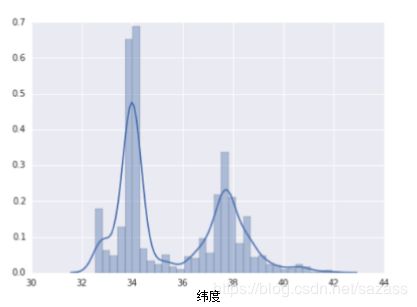
在数据集中，latitude 是一个浮点值。不过，在我们的模型中将 latitude 表示为浮点特征没有意义。这是因为纬度和房屋价值之间不存在线性关系。例如，纬度 35 处的房屋并不比纬度 34 处的房屋贵 35/34（或更便宜）。但是，纬度或许能很好地预测房屋价值。

为了将纬度变为一项实用的预测指标，我们对纬度“分箱”，如下图所示：

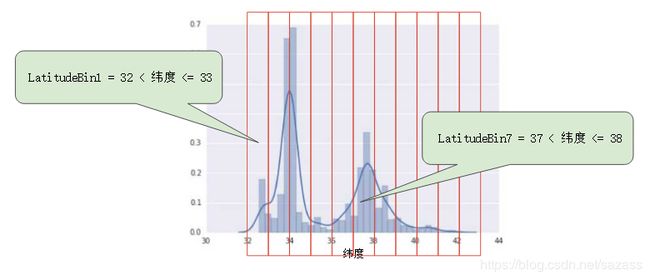
我们现在拥有 11 个不同的布尔值特征（LatitudeBin1、LatitudeBin2、…、LatitudeBin11），而不是一个浮点特征。拥有 11 个不同的特征有点不方便，因此我们将它们统一成一个 11 元素矢量。这样做之后，我们可以将纬度 37.4 表示为：
[0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0]
分箱之后，我们的模型现在可以为每个纬度学习完全不同的权重。

清查

截至目前，我们假定用于训练和测试的所有数据都是值得信赖的。在现实生活中，数据集中的很多样本是不可靠的，原因有以下一种或多种：

遗漏值。 例如，有人忘记为某个房屋的年龄输入值。
重复样本。 例如，服务器错误地将同一条记录上传了两次。
不良标签。 例如，有人错误地将一颗橡树的图片标记为枫树。
不良特征值。 例如，有人输入了多余的位数，或者温度计被遗落在太阳底下。

一旦检测到存在这些问题，您通常需要将相应样本从数据集中移除，从而“修正”不良样本。要检测遗漏值或重复样本，您可以编写一个简单的程序。检测不良特征值或标签可能会比较棘手。

除了检测各个不良样本之外，您还必须检测集合中的不良数据。直方图是一种用于可视化集合中数据的很好机制。此外，收集如下统计信息也会有所帮助：
最大值和最小值
均值和中间值
标准偏差

遵循以下规则：

1.记住您预期的数据状态。
2.确认数据是否满足这些预期（或者您可以解释为何数据不满足预期）。
3.仔细检查训练数据是否与其他来源（例如信息中心）的数据一致。

像处理任何任务关键型代码一样谨慎处理您的数据。良好的机器学习依赖于良好的数据