最简单易懂的10堂算法入门课——算法是什么

算法太重要了

“人工智能”，“机器学习”，“大数据”，这些越来越常听到的字眼，背后其实都是一个个“算法”。

诸多高新科技，似乎都离不开“算法”的“加持”。

科学家 / 工程师 / 技术人员，现在如果不懂点算法，都不太好意思了。

算法其实很容易

听着这么高大上的“算法”其实一点也不难学！

为啥讲算法的书却很难看懂？

就是讲得太复杂了么，不同编程语言还都不一样。

专栏特点

1. 语言和逻辑极简，化复杂为通俗易懂，极速掌握；

2. 不使用编程语言！是的，这才是算法入门的最速方法；

3. 直击算法思维的核心点，不在次要知识上浪费时间。

 

什么是“算法”

算法，一看字面就知道，肯定是“计算方法”的简称啦，特指“计算机的计算方法”，所以，算法是由电脑程序来实现的。

算法，英文叫Algorithm，就是为了让电脑解决一个问题而设计出来的一套计算方法，这套计算方法的设计是依靠“数学模型”的建立。

也就是说，程序员在设计算法之前，会将实际问题理解分析，归纳为一个“具体的数学问题”。

算法是解决问题的计算方法

算法有这么几个特征

1 确定

算法的每一个步骤都有“明确的意义”，对于算法结果的预期也是明确的。

2 有穷

算法不能一直算，停不下来是不行的；要有一个明确的结束条件，要不然算到“天荒地老”还有什么意义呢？

3 可行

有个笑话说一个人面试会计师，算数特别快瞬间出结果，但是就是算得不对。

4 输入输出

算法就是用来解决问题的，问题的来源就是输入，问题的结果就是输出。

再复杂的算法也是由一个个小算法组合成的

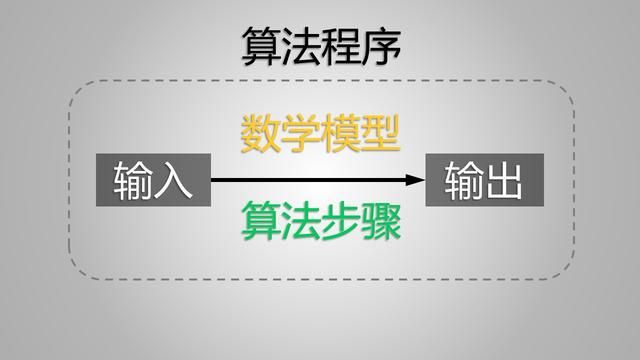
怎么设计一个算法程序呢

算法有三个要素——

数学模型，输入输出方法，算法步骤。

 

所以说，怎么设计一个算法呢？

首先，先对要解决的问题建立一个数学模型，把原问题化为数学问题；

然后，将问题的“已知条件”化为“数据”输入到数学模型中；

再然后，通过对输入一步一步的转化/处理/计算，得到结果；

最后，把结果按照希望的形式，输出出来。

举个例子吧

比如我们要解决一个问题——班级里有30个同学，我们现在知道他们的姓名和考试分数，比如小红90分，小刚97分，小明60分等等，求班级里面哪位同学成绩最好？

谁的成绩最好呢？

那么我们按照上面的步骤来设计一个小算法吧。

1 把原问题转化为数学问题

求30个成绩值中的最大值及对应的姓名；

2 已知条件化为输入数据

依次输入30个名字和30个成绩值；（其中名字的数据类型为字符串，成绩值的数据类型为整数型，关于数据类型我们将在后面详细讲解）

3 分步计算

这是一个典型的求最大值的问题，方法很多，这里举一种方法：

3-1 取出第1个同学和第2个同学的姓名和成绩，比较大小，将那个较大的成绩值储存在一个位置，这个位置我们给他起个名字，就叫<当前最大成绩值>吧，再把这个较好的成绩对应的同学姓名存到另一个位置，就叫<当前最好成绩的同学姓名>；

3-2 这样，第1个同学和第2个同学成绩比较完成，得到了这2名同学中的成绩最好的同学，信息储存在：<当前最大成绩值>和<当前最好成绩的同学姓名>中；

3-3 下面就是重复性的工作了，把得到的<当前最大成绩值>和<当前最好成绩的同学姓名>与第3位同学进行比较，仍然是把较大的成绩值储存在<当前最大成绩值>里，把这个较好的成绩对应的同学姓名存到<当前最好成绩的同学姓名>里；

3-4 这个过程一直进行，直到把30个同学的信息都比较完，这时<当前最大成绩值>里存的值就是最好的成绩，<当前最好成绩的同学姓名>里存的值就是这位最厉害的同学的姓名。

4 输出

按照你想要的格式，将上面两个储存的值显示出来，就完成了！

借上面的例子有几点要说明一下

1 解决同一个问题，可能有各种各样的算法。不同的算法，可能执行速度不同，可能编写难易度不同，可能占用的资源不同，甚至可能计算准确度都不同；很多时候并没有最好的算法，只有在特定条件下最适合的算法。

2 每一个算法都有适用的条件，条件变了，算法可能就用好用了。比如上面例子，如果这个班级中有2个同学的成绩刚好一样，那么按理说就应该输出两个姓名和成绩，上面的算法就需要改进一下了。

算法 —— 一个强逻辑体

3 能把问题具体化为一个或几个数学问题，问题就解决了一半。就如同学习和工作中一样，所谓解决问题的能力，有一半是分析问题的能力，能够将大问题分解成小问题，将抽象问题等价为具体问题。