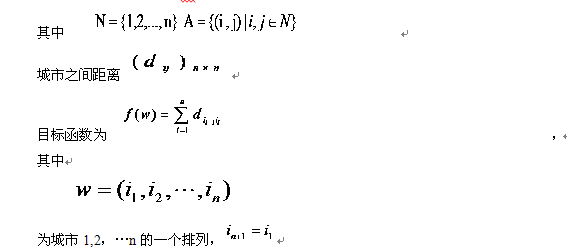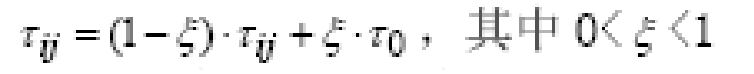ACS蚁群算法求解对称TSP旅行商问题的JavaScript实现

    本来以为在了解蚁群算法的基础上实现这道奇怪的算法题并不难，结果实际上大相径庭啊。做了近三天时间，才改成现在这能勉强拿的出手的模样。由于公式都是图片，暂且以截图代替那部分内容吧，mark一记。

 

1 蚁群算法

(1) 蚁群AS算法简介

      20世纪90年代意大利学者M．Dorigo，V．Maniezzo，A．Colorni等从生物进化的机制中受到启发，通过模拟自然界蚂蚁搜索路径的行为，提出来一种新型的模拟进化算法—— 蚁群算法，是群智能理论研究领域的一种主要算法。用该方法求解TSP问题、分配问题、job-shop调度问题，取得了较好的试验结果．虽然研究时间不长，但是现在的研究显示出，蚁群算法在求解复杂优化问题（特别是离散优化问题）方面有一定优势，表明它是一种有发展前景的算法。

      这种方法能够被用于解决大多数优化问题或者能够转化为优化求解的问题。现在其应用领域已扩展到多目标优化、数据分类、数据聚类、模式识别、电信QoS管理、生物系统建模、流程规划、信号处理、机器人控制、决策支持以及仿真和系统辩识等方面，群智能理论和方法为解决这类应用问题提供了新的途径。

(2) 蚁群AS算法过程

      蚁群算法是对自然界蚂蚁的寻径方式进行模似而得出的一种仿生算法。蚂蚁在运动过程中，能够在它所经过的路径上留下一种称之为外激素(pheromone)的物质进行信息传递，而且蚂蚁在运动过程中能够感知这种物质，并以此指导自己的运动方向，因此由大量蚂蚁组成的蚁群集体行为便表现出一种信息正反馈现象：某一路径上走过的蚂蚁越多，则后来者选择该路径的概率就越大。

     为了说明蚁群算法的原理，先简要介绍一下蚂蚁搜寻食物的具体过程。在蚁群寻找食物时，它们总能找到一条从食物到巢穴之间的最优路径。这是因为蚂蚁在寻找路径时会在路径上释放出一种特殊的信息素。当它们碰到一个还没有走过的路口时．就随机地挑选一条路径前行。与此同时释放出与路径长度有关的信息素。路径越长，释放的激索浓度越低.当后来的蚂蚁再次碰到这个路口的时候．选择激素浓度较高路径概率就会相对较大。这样形成一个正反馈。最优路径上的激索浓度越来越大．而其它的路径上激素浓度却会随着时间的流逝而消减。最终整个蚁群会找出最优路径。

 

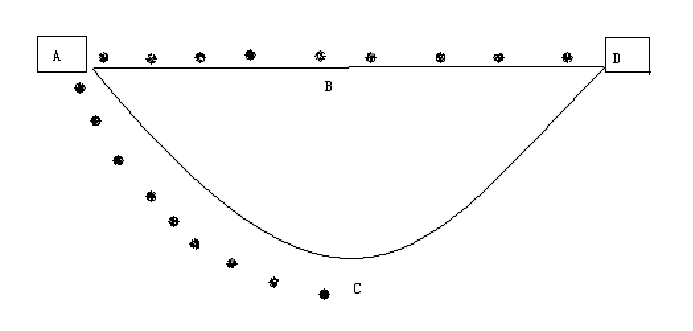
图1 蚂蚁单次行走示意图

      蚂蚁从A点出发，速度相同，食物在D点，可能随机选择路线ABD或ACD。假设初始时每条分配路线一只蚂蚁，每个时间单位行走一步，本图为经过9个时间单位时的情形：走ABD的蚂蚁到达终点，而走ACD的蚂蚁刚好走到C点，为一半路程。

 

图2 蚂蚁来回行走示意图

      图2为从开始算起，经过18个时间单位时的情形：走ABD的蚂蚁到达终点后得到食物又返回了起点A，而走ACD的蚂蚁刚好走到D点。

假设蚂蚁每经过一处所留下的信息素为一个单位，则经过36个时间单位后，所有开始一起出发的蚂蚁都经过不同路径从D点取得了食物，此时ABD的路线往返了2趟，每一处的信息素为4个单位，而 ACD的路线往返了一趟，每一处的信息素为2个单位，其比值为2：1。

      寻找食物的过程继续进行，则按信息素的指导，蚁群在ABD路线上增派一只蚂蚁（共2只），而ACD路线上仍然为一只蚂蚁。再经过36个时间单位后，两条线路上的信息素单位积累为12和4，比值为3：1。

      若按以上规则继续，蚁群在ABD路线上再增派一只蚂蚁（共3只），而ACD路线上仍然为一只蚂蚁。再经过36个时间单位后，两条线路上的信息素单位积累为24和6，比值为4：1。

      若继续进行，则按信息素的指导，最终所有的蚂蚁会放弃ACD路线，而都选择ABD路线。这也就是前面所提到的正反馈效应。

(3) 蚁群AS算法TSP问题应用

      基于以上蚁群寻找食物时的最优路径选择问题，可以构造人工蚁群，来解决最优化问题，如TSP问题。

      人工蚁群中把具有简单功能的工作单元看作蚂蚁。二者的相似之处在于都是优先选择信息素浓度大的路径。较短路径的信息素浓度高，所以能够最终被所有蚂蚁选择，也就是最终的优化结果。两者的区别在于人工蚁群有一定的记忆能力，能够记忆已经访问过的节点。同时，人工蚁群再选择下一条路径的时候是按一定算法规律有意识地寻找最短路径，而不是盲目的。例如在TSP问题中，可以预先知道当前城市到下一个目的地的距离。

TSP问题表示为一个N个城市的有向图G=（N，A），

 

      TSP问题的人工蚁群算法中，假设m只蚂蚁在图的相邻节点间移动，从而协作异步地得到问题的解。每只蚂蚁的一步转移概率由图中的每条边上的两类参数决定：

      1．  信息素值 也称信息素痕迹。

      2．  可见度，即先验值。

      信息素的更新方式有2种，一是挥发，也就是所有路径上的信息素以一定的比率进行减少，模拟自然蚁群的信息素随时间挥发的过程；二是增强，给评价值“好”(有蚂蚁走过)的边增加信息素。

蚂蚁向下一个目标的运动是通过一个随机原则来实现的，也就是运用当前所在节点存储的信息，计算出下一步可达节点的概率，并按此概率实现一步移动，逐此往复，越来越接近最优解。

      蚂蚁在寻找过程中，或者找到一个解后，会评估该解或解的一部分的优化程度，并把评价信息保存在相关连接的信息素中。                     。

 

(4) 蚁群算法应用于TSP步骤

2蚁群系统(Ant Colony System, ACS)

(1) 蚁群系统

      为了进一步克服AS中暴露出的问题，提出了蚁群系统(Ant Colony System, ACS)。该系统的提出是以Ant-Q算法为基础的。Ant-Q将蚂蚁算法和一种增强型学习算法Q-learning有机的结合了起来。ACS与AS之间存在三方面的主要差异：首先，ACS采用了更为大胆的行为选择规则；其次，只增强属于全局最优解的路径上的信息素。其中，0<ρ<1是信息素挥发参数， 是从寻路开始到当前为止全局最优的路径长度。

      再次，还引入了负反馈机制，每当一只蚂蚁由一个节点移动到另一个节点时，该路径上的信息素都按照如下公式被相应的消除一部分，从而实现一种信息素的局部调整，以减小已选择过的路径再次被选择的概率。

(2) ACS解决TSP问题

      在本文中，使用ACS解决对称TSP问题，具体的解题步骤如下：

      A.初始化全局参数

      n:城市数n，

      m:蚂蚁只数m (用随机数取n^0.5 ~ n/2之间的值),

      p:信息素蒸发系数p=0.7，

      NC,NC_max:初始外循环次数NC=1，最大循环次数NC_max=60，

      D:用坐标计算两两城市之间的距离矩阵D，

      T:初始城市路线之间的信息素浓度矩阵T(初始默认相等，均为1/(n*(n-1)),即和为1)，

      E:每只蚂蚁前进时的城市路线信息素浓度矩阵E(每一轮均为当时的T，假设每一轮的蚂蚁之间相互影响极小，忽略不计，留下的信息素主要对后面的蚂蚁起作用)，

      last,lastRoute:用于存储当前最优路线的总长度last和最优过程lastRoute。

      B.外循环

      循环变量为轮数NC。每一次外循环均初始化当前轮数当前蚂蚁i的行走路径。每一次内循环结束之后计算当前NC下每只蚂蚁的总行走长度sAll，记录每只蚂蚁的行走过程并由此得到当前最短的行走总长度last和路线lastRoute，之后按照公式1相对增强当前最佳路线的信息素，挥发其它路线信息素，再进入下一轮。

      C.内循环

      对于每一只蚂蚁i，记录它们的需要访问城市列表route。

默认从城市0出发(从哪儿出发其实都一样)，按照到其它城市信息素的比例随机选择下一个城市。具体做法为求出下一个城市到当前城市的距离比上总的距离之和，然后逐个累加，于是求得比例区间[0 ~ p1 , p1 ~ p1 + p2 , p1 + p2 ~ p1 + p2 + p3......1]。用Math.random函数取0~1之间的随机值判断在哪个区间，则下一步走到对应的城市。然后将route中对应的城市置0，并将已选城市与原始城市之间的距离置0，重新计算比例区间的时候即可不影响，当route中所有的数值之和为0时说明除了初始城市全部都访问了，最后访问初始城市0，一只蚂蚁即完成使命。

3 具体实现

      根据以上算法过程，可以写出程序如下：

(1)  Functions.js

      自定义工具函数，减少全局对象，尽可能代码重用。

      其中：

      minAll(arr)： 返回一维数组arr中的最小值

      all(arr) ：一维数组arr求和

      nextStep(x,E)： 根据当前城市x和所有路径信息素的浓度矩阵E随机确定下一座城市，类似转盘法。详细算法见上面2.(2).C。

      sum(x,E) ：配合nextStep实现转盘效果

      new2Arr(arr,x)： 将undefined类型的新建arr转化为二维数组，一般用来初始化

      getAntNum(x) ：通过城市数量得到最佳蚂蚁数量

      getType(o) , extend(destination,source)： 实现对象的深复制，尤其针对多维数组(一般情况下的一维的用slice或者concat就行)，见参考文献[6]。

(2)  AntSystem.js

      ACS蚁群算法的具体实现，封装于AntSystem(C)中，便于调用。输入城市坐标矩阵C，输入最优路径总长度last和最优路径lastRoute。

(3)  Action.js

      利用jquery.js工具库实现自定义数据输入和最终结果展现。有部分数据类型判断。(基于关注算法本身的准则，仅对输入的蚂蚁数量n有一定的判断和提示)

(4)  Jquery-1.11.0.js

      一种流行的js库，用于js快速兼容开发

 

4 算法测试

      点击default.html 按照提示输入数据一步步提交即可。兼容IE8.0+，firefox，chrome等浏览器。

      运行过程截图：

1. 输入合适数目后点击确认弹出坐标矩阵输入窗口

 

 

      2.输入坐标矩阵点击确认得到最终的结果

      输入为(0,0), (0,1), (0,2), (0,3), (0,4), (1,0), (1,1), (1,2), (1,3), (2,2), (2,3), (2,4), (3,3), (3,4)。

 

 

      3.在FF的控制台脚本中合适的地方设置断点可以单步查看具体的运行过程(由于具体展示出来过于占据篇幅，全部输出网页显示过于琐细，这儿列一张图)(可以按照需要将每一轮的重要数据抽取出来查看具体变化)

 

 

 

5 分析和总结

      本次ACS解决对称TSP问题的javascript实现，相对于经典的ACS，有一些修改的地方：

      1.外循环结束条件只有循环轮数NC

      2.采用参考文献[4]上的推荐挥发系数p值，不是多次数据测量确认。

 

      Js作为一种弱变量的语言，拥有一些隐性默认的规则：

      1.使用+符号时可能会默认将两边变量的数据类型改为string。参见参考文献[7]。

      2.在函数内部申明变量x时，如果不使用var语句而是直接给变量x赋值会导致变量x变为全局变量，污染全局空间。

      3.函数的参数在函数内部作为局部变量存在，当函数结束时结束（除非使用闭包），不会对外面同名变量产生影响。

      4.对象变量之间使用=号是对象的引用传递，即两个对象指向内存中同一块区域，当一个变量改变对象的属性时，另外一个变量对应的属性也会变。因此，需要用到对象的深复制。对于一维数组使用slice和concat函数，对于多维数组参照参考文献[6]。

6 参考文献

      [1] 彭喜元 彭宇 戴毓丰. 群智能理论及应用. 电子学报, 2003年 S1期.

      [2] 李士勇. 蚁群算法及其应用. 哈工大出版社.

      [3] 吴启迪. 智能蚁群算法及应用. 上海科技出版社.

      [4] 詹士昌,徐婕,吴俊. 蚁群算法中有关算法参数的最优选择[J]. 科技通报,2003,05:381-386.

      [5] 宋志飞. 基于蚁群算法的TSP问题研究[D].江西理工大学,2013.

      [6] js深复制http://www.cnblogs.com/Loofah/archive/2012/03/23/2413665.html

      [7] js类型转换http://weibo.com/p/230418c3aa9eb60102vh10#_loginLayer_1436233053863

 

      具体的源码可以在我的github上下载 https://github.com/codetker/AntSystem 。

      由于最近开始实习，得先完成公司手头的工作(忙里偷闲才是真闲，，，)。所以后续的想法：在不同的浏览器中对算法执行平均速度的测试，以及用C和matlab对于同一代码的平均执行时间的比较，还有 线性神经网络实现spammer判断系统的JavaScript实现，估计得要一段时间才能出炉咯。

      鉴于我对许多JavaScript内置函数不熟悉，代码里面肯定有很多的弯路，求大家指出来，谢谢。

 

转载于:https://www.cnblogs.com/codetker/p/4627167.html