2020牛客寒假算法基础集训营3 【A - J】

题目来源：https://ac.nowcoder.com/acm/contest/3004#question

实力是7题吧，有2题题目都没看… 今天主要被G搞了心态，一个取模没取 debug2个小时，枯了…好玩的是那个汉诺塔 打表找规律233（可能不是正解）

---

A - 牛牛的DRB迷宫I

一个二维递推的dp,全场题，不多解释了。

 #include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#define ls k<<1,l,mid
#define rs k<<1|1,mid+1,r
#define mp(x,y) make_pair(x,y)
#define r(x) read(x)
#define rrr(x,y,z) read(x);read(y);read(z)
#define FOR(i,l,r) for(int i=l;i<=r;i++)
using namespace std;
typedef long long LL;
typedef pair<int,int> pt;
const int N=1e6+5;
const int M=2e3+5;
const int INF=0x7fffffff;
const int mod=1e9+7;
const double eps=1e-8;
const double pi=acos(-1);
LL n,m;
LL dp[M][M];
char s[M][M];
template<class T>
inline void read(T &x)
{
    char c; x=1;
    while((c=getchar())<'0'||c>'9') if(c=='-') x=-1;
    T res=c-'0';
    while((c=getchar())>='0'&&c<='9') res=res*10+c-'0';
    x*=res;
}
int main()
{
    r(n); r(m);
    FOR(i,1,n){
        scanf("%s",s[i]+1);
    }
    dp[1][1]=1;
    FOR(i,1,n){
        FOR(j,1,m){
            if(s[i][j]=='R'){
                dp[i][j+1]=(dp[i][j+1]+dp[i][j])%mod;
            }
            else if(s[i][j]=='D'){
                dp[i+1][j]=(dp[i+1][j]+dp[i][j])%mod;
            }
            else{
                dp[i][j+1]=(dp[i][j+1]+dp[i][j])%mod;
                dp[i+1][j]=(dp[i+1][j]+dp[i][j])%mod;
            }
        }
    }
    cout<<dp[n][m]<<endl;
    return 0;
}

---

B - 牛牛的DRB迷宫II

这题真的好神奇，长见识了！感谢出题的dalao，orz

我们就构造一个特殊的方阵，它的主对角线上都是B，主对角线下面一条都是R，上面一条都是D，那么假如其他的都是R，此时主对角线上能走到的是不是1 2 4 8

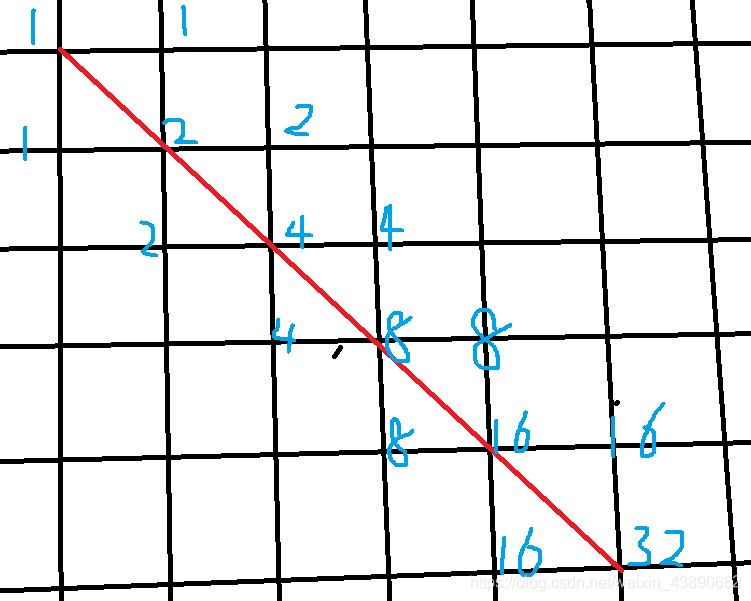
红色的线为主对角线，可见这种方式可以构造出所有的2ⁱ，那怎么构造其他的呢？
现在我们来构造25，绿线表示出了之前的路 额外可达的路

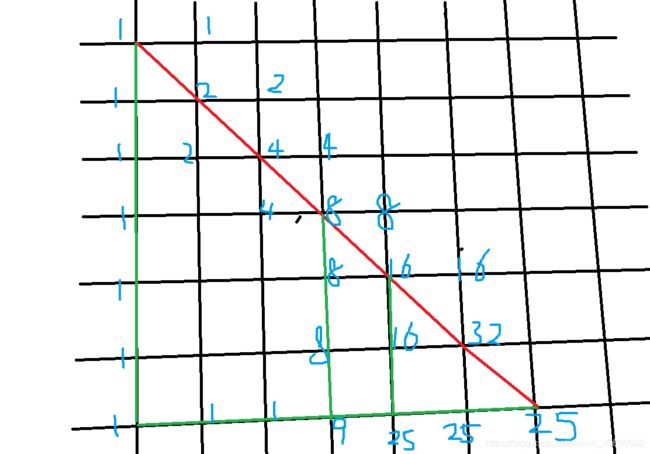
就是标记25的哪些位有1，然后一个一条路下来就好了

#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#define ls k<<1,l,mid
#define rs k<<1|1,mid+1,r
#define mp(x,y) make_pair(x,y)
#define r(x) read(x)
#define rrr(x,y,z) read(x);read(y);read(z)
#define FOR(i,l,r) for(int i=l;i<=r;i++)
using namespace std;
typedef long long LL;
typedef pair<LL,LL> pt;
const int N=1e5+5;
const int M=2e3+5;
const int INF=0x7fffffff;
const int mod=1e9+7;
const double eps=1e-8;
const double pi=acos(-1);
LL n,m;
bool vis[M];
char s[M][M];
template<class T>
inline void read(T &x)
{
    char c; x=1;
    while((c=getchar())<'0'||c>'9') if(c=='-') x=-1;
    T res=c-'0';
    while((c=getchar())>='0'&&c<='9') res=res*10+c-'0';
    x*=res;
}
int main()
{
    LL k;
    r(k);
    k%=mod;
    if(k==0){
        cout<<2<<' '<<2<<endl;
        cout<<"RR\n";
        cout<<"RR\n";
    }
    n=0;
    while(k){
        n++;
        if(k&1) vis[n]=1;
        k>>=1;
    }
    FOR(i,1,n){
        s[i][i]='B';
    }
    FOR(i,1,n-1){
        s[i][i+1]='D';
        s[i+1][i]='R';
    }
    n++;
    FOR(i,1,n){
        if(vis[i]){
            s[i+1][i]='B';
            FOR(j,i+2,n) s[j][i]='D';
            FOR(j,1,n) s[n][j]='R';
        }
    }
    cout<<n<<' '<<n<<endl;
    FOR(i,1,n){
        FOR(j,1,n){
            if(s[i][j]==0) s[i][j]='R';
            cout<<s[i][j];
        }
        cout<<endl;
    }
    return 0;
}

---

C - 牛牛的数组越位

模拟题，不是大模拟还好…

#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#define ls k<<1,l,mid
#define rs k<<1|1,mid+1,r
#define mp(x,y) make_pair(x,y)
#define r(x) read(x)
#define rrr(x,y,z) read(x);read(y);read(z)
#define FOR(i,l,r) for(int i=l;i<=r;i++)
using namespace std;
typedef long long LL;
typedef pair<int,int> pt;
const int N=1e6+5;
const int M=2e3+5;
const int INF=0x7fffffff;
const int mod=1e9+7;
const double eps=1e-8;
const double pi=acos(-1);
LL n,m;
LL f[1005][1005];
template<class T>
inline void read(T &x)
{
    char c; x=1;
    while((c=getchar())<'0'||c>'9') if(c=='-') x=-1;
    T res=c-'0';
    while((c=getchar())>='0'&&c<='9') res=res*10+c-'0';
    x*=res;
}
int main()
{
    int t,k;
    r(t);
    while(t--){
        rrr(n,m,k);
        FOR(i,1,n){
            FOR(j,1,m) f[i][j]=0;
        }
        bool err=0;
        bool noot=0;
        while(k--){
            int a,b,c;
            rrr(a,b,c);
            if(a<0||a>=n||b<0||b>=m){
                noot=1;
            }
            LL pos=a*m+b;
            //cout<
            if(pos<0||pos>=n*m){
                err=1;
                continue;
            }
            LL px=pos/m;
            LL py=pos%m;
            f[px+1][py+1]=c;
        }
        if(err){
            cout<<"Runtime error\n";
        }
        else{
            FOR(i,1,n){
                FOR(j,1,m) cout<<f[i][j]<<' ';
                cout<<endl;
            }
            if(noot) cout<<"Undefined Behaviour\n";
            else cout<<"Accepted\n";
        }
    }
    return 0;
}

---

D - 牛牛与二叉树的数组存储

题目看错了 坑了2发罚时…

#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#define ls k<<1,l,mid
#define rs k<<1|1,mid+1,r
#define mp(x,y) make_pair(x,y)
#define r(x) read(x)
#define rrr(x,y,z) read(x);read(y);read(z)
#define FOR(i,l,r) for(int i=l;i<=r;i++)
using namespace std;
typedef long long LL;
typedef pair<int,int> pt;
const int N=1e6+5;
const int M=2e3+5;
const int INF=0x7fffffff;
const int mod=1e9+7;
const double eps=1e-8;
const double pi=acos(-1);
LL n,m;
int f[N];
struct node
{
    int id,pos;
}g[N];
template<class T>
inline void read(T &x)
{
    char c; x=1;
    while((c=getchar())<'0'||c>'9') if(c=='-') x=-1;
    T res=c-'0';
    while((c=getchar())>='0'&&c<='9') res=res*10+c-'0';
    x*=res;
}
bool cmp(node a,node b)
{
    return a.id<b.id;
}
int main()
{
    r(n);
    memset(f,-1,sizeof f);
    int cnt=0;
    FOR(i,1,n){
        r(f[i]);
        if(f[i]>0){
            g[++cnt].pos=i;
            g[cnt].id=f[i];
        }
    }
    sort(g+1,g+cnt+1,cmp);
    cout<<"The size of the tree is "<<cnt<<endl;
    if(cnt) printf("Node %d is the root node of the tree\n",f[1]);
    for(int i=1;i<=cnt;i++){
        int now=g[i].pos;
        printf("The father of node %d is %d, the left child is %d, and the right child is %d\n",i,f[now/2],f[now<<1],f[now<<1|1]);
    }
    return 0;
}

---

E - 牛牛的随机数

数据实在是太大了，我们不能从数上考虑，要从位入手，考虑二进制
有一个规律，假如说现在是第k位（从右往左），那么这一位在数中的分布周期为1<。比如第一位的周期为2，呈01010101的分布，这也是奇偶数的划分条件。 知道这个规律我们可以求 1 - n的数里面有多少个数 的第k位为1，这是写这题很重要的一部分。
然后既然是随机，那所有情况都要考虑到对不对，也就是说，所有的位也会和其他所有的位异或，那我们就从位来看。假如这一位与另一个数的这一位异或值为1，代表这两位异或对答案有贡献。
现在考虑第k位的贡献，假如[ l1 , r1 ]的所有数里面第k位有x个1，y个0 （显然x+y=r1-l1+1) ，[ l2 , r2 ]的所有数里面第k位有p个1，q个0 ，那么贡献不就是(x*q+y*p)*(1<吗
枚举1 - 60 位即可~

---

F - 牛牛的Link Power I

前缀和可以O(n) 解决 线段树也可以写（见G题）

#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#define ls k<<1,l,mid
#define rs k<<1|1,mid+1,r
#define mp(x,y) make_pair(x,y)
#define r(x) read(x)
#define rrr(x,y,z) read(x);read(y);read(z)
#define FOR(i,l,r) for(int i=l;i<=r;i++)
using namespace std;
typedef long long LL;
typedef pair<int,int> pt;
const int N=1e6+5;
const int M=2e3+5;
const int INF=0x7fffffff;
const int mod=1e9+7;
const double eps=1e-8;
const double pi=acos(-1);
LL n,m;
char s[N];
LL f[N];
LL sum[N];
template<class T>
inline void read(T &x)
{
    char c; x=1;
    while((c=getchar())<'0'||c>'9') if(c=='-') x=-1;
    T res=c-'0';
    while((c=getchar())>='0'&&c<='9') res=res*10+c-'0';
    x*=res;
}
int main()
{
    r(n); scanf("%s",s+1);
    int cnt=0;
    FOR(i,1,n){
        if(s[i]=='1') f[++cnt]=i;
    }
    FOR(i,1,cnt){
        sum[i]=sum[i-1]+f[i];
        //cout<
        }
    LL ans=0;
    FOR(i,1,cnt){
       // cout<
        ans=(ans+sum[cnt]-sum[i]-(cnt-i)*f[i]%mod+mod)%mod;
    }
    cout<<ans<<endl;
    return 0;
}

---

G - 牛牛的Link Power II

建两个线段树分别维护 和 和 个数 每次查询加减那个点的贡献就好了

#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#define ls k<<1,l,mid
#define rs k<<1|1,mid+1,r
#define mp(x,y) make_pair(x,y)
#define r(x) read(x)
#define rrr(x,y,z) read(x);read(y);read(z)
#define FOR(i,l,r) for(int i=l;i<=r;i++)
using namespace std;
typedef long long LL;
typedef pair<LL,LL> pt;
const int N=1e5+5;
const int M=2e3+5;
const int INF=0x7fffffff;
const int mod=1e9+7;
const double eps=1e-8;
const double pi=acos(-1);
int f[N],g[N];
LL sum[N<<2],num[N<<2];
char s[N];
LL n,m;
template<class T>
inline void read(T &x)
{
    char c; x=1;
    while((c=getchar())<'0'||c>'9') if(c=='-') x=-1;
    T res=c-'0';
    while((c=getchar())>='0'&&c<='9') res=res*10+c-'0';
    x*=res;
}
void build(int k,int l,int r)
{
    if(l==r){
        sum[k]=f[l];
        num[k]=g[l];
        return ;
    }
    int mid=(l+r)>>1;
    build(ls); build(rs);
    sum[k]=(sum[k<<1]+sum[k<<1|1])%mod;
    num[k]=(num[k<<1]+num[k<<1|1])%mod;
}
void update(int k,int l,int r,int pos,int op)
{
    if(l==r){
        if(op==1){sum[k]=pos; num[k]=1;}
        else if(op==2){sum[k]=0; num[k]=0;}
        return ;
    }
    int mid=(l+r)>>1;
    if(mid>=pos) update(ls,pos,op);
    else update(rs,pos,op);
    sum[k]=(sum[k<<1]+sum[k<<1|1])%mod;
    num[k]=(num[k<<1]+num[k<<1|1])%mod;
}
LL query1(int k,int l,int r,int x,int y)
{
    if(x<=l&&r<=y){
        return sum[k];
    }
    int mid=(l+r)>>1;
    LL res=0;
    if(mid>=x) res=(res+query1(ls,x,y))%mod;
    if(mid<y) res=(res+query1(rs,x,y))%mod;
    return res;
}
LL query2(int k,int l,int r,int x,int y)
{
    if(x<=l&&r<=y){
        return num[k];
    }
    int mid=(l+r)>>1;
    LL res=0;
    if(mid>=x) res=(res+query2(ls,x,y))%mod;
    if(mid<y) res=(res+query2(rs,x,y))%mod;
    return res;
}
int main()
{
    r(n);
    scanf("%s",s+1);
    r(m);
    FOR(i,1,n){
        if(s[i]=='1'){
            f[i]=i;
            g[i]=1;
        }
        else{f[i]=0; g[i]=0;}
    }
    build(1,1,n);
    LL ans=0;
    FOR(i,1,n-1){
        if(f[i]!=0) ans=(ans+query1(1,1,n,i,n)-query2(1,1,n,i,n)*f[i])%mod;
    }
    cout<<ans<<endl;
    while(m--){
        int op,a;
        r(op); r(a);
        update(1,1,n,a,op);
        LL ans1=0,ans2=0;
        if(a>1) ans1=(1ll*query2(1,1,n,1,a-1)*a%mod-1ll*query1(1,1,n,1,a-1)+mod)%mod;
        if(a<n) ans2=(1ll*query1(1,1,n,a+1,n)-1ll*query2(1,1,n,a+1,n)*a%mod+mod)%mod;
//        FOR(j,1,10) cout<
//        cout<
//        if(a>1) cout<
        if(op==1) ans=(ans+ans1+ans2)%mod;
        else if(op==2) ans=(ans-ans1-ans2+mod+mod)%mod;
        cout<<ans<<endl;
    }
    return 0;
}

---

H - 牛牛的k合因子数

埃氏筛标记出所有的合数 然后大循环枚举i 小循环枚举其因子 复杂度O(n^3/2)

#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#define ls k<<1,l,mid
#define rs k<<1|1,mid+1,r
#define mp(x,y) make_pair(x,y)
#define r(x) read(x)
#define rrr(x,y,z) read(x);read(y);read(z)
#define FOR(i,l,r) for(int i=l;i<=r;i++)
using namespace std;
typedef long long LL;
typedef pair<int,int> pt;
const int N=1e6+5;
const int M=2e3+5;
const int INF=0x7fffffff;
const int mod=1e9+7;
const double eps=1e-8;
const double pi=acos(-1);
LL n,m;
int num[N];
bool isp[N];
int p[N];
template<class T>
inline void read(T &x)
{
    char c; x=1;
    while((c=getchar())<'0'||c>'9') if(c=='-') x=-1;
    T res=c-'0';
    while((c=getchar())>='0'&&c<='9') res=res*10+c-'0';
    x*=res;
}
int main()
{
    r(n); r(m);
    int cnt=0;
    FOR(i,1,n) isp[i]=1;
    FOR(i,2,n){
        if(isp[i]){
            p[++cnt]=i;
            for(int j=2*i;j<=n;j+=i) isp[j]=0;
        }
    }
    //FOR(i,1,n) cout<
    //cout<
    FOR(i,1,n){
        int now=i;
        int res=0;
        for(int j=2;j<=sqrt(now);j++){
            if(now%j==0){
                if(j==sqrt(now)){
                    if(isp[j]==0) res++;
                }
                else{
                    if(isp[j]==0) res++;
                    if(isp[now/j]==0) res++;
                }
            }
        }
        if(isp[now]==0) res++;
        //cout<
        num[res]++;
    }
    while(m--){
        int a; r(a);
        cout<<num[a]<<endl;
    }
    return 0;
}

---

I - 牛牛的汉诺塔

这题我一开始真不会写，但是盯着打出来的表看了十几分钟就想到了233
我也不知道为什么，看我的代码吧 （打表找规律）

#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#define ls k<<1,l,mid
#define rs k<<1|1,mid+1,r
#define mp(x,y) make_pair(x,y)
#define r(x) read(x)
#define rrr(x,y,z) read(x);read(y);read(z)
#define FOR(i,l,r) for(int i=l;i<=r;i++)
using namespace std;
typedef long long LL;
typedef pair<int,int> pt;
const int N=1e5+5;
const int M=2e3+5;
const int INF=0x7fffffff;
const int mod=1e9+7;
const double eps=1e-8;
const double pi=acos(-1);
LL dp[M][7];
template<class T>
inline void read(T &x)
{
    char c; x=1;
    while((c=getchar())<'0'||c>'9') if(c=='-') x=-1;
    T res=c-'0';
    while((c=getchar())>='0'&&c<='9') res=res*10+c-'0';
    x*=res;
}
int main()
{
    int n;
    FOR(i,1,6) dp[1][i]=0;
    FOR(i,1,6) dp[2][i]=0;
    dp[1][2]=dp[2][2]=dp[2][1]=dp[2][4]=1;
    dp[1][0]=1;
    dp[2][0]=3;
    r(n);
    FOR(i,3,n){
        FOR(j,1,6){
            if(j==1||j==4){
                if(i&1){
                    dp[i][j]=dp[i-1][j];
                }
                else dp[i][j]=dp[i-1][2]+dp[i-1][3];
            }
            else if(j==3||j==6){
                if(i&1){
                    dp[i][j]=dp[i-1][5]+dp[i-1][4];
                }
                else dp[i][j]=dp[i-1][j];
            }
            else if(j==2){
                if(i&1){
                    dp[i][j]=dp[i-1][j]+1+dp[i-1][1]+dp[i-1][3];
                }
                else dp[i][j]=dp[i-1][j];
            }
            else if(j==5){
                if(i&1){
                    dp[i][j]=dp[i-1][j];
                }
                else dp[i][j]=dp[i-1][j]+dp[i-1][4]+dp[i-1][6];
            }
        }
        dp[i][0]=dp[i-1][0]*2+1;
    }
//    FOR(i,1,n){
//        FOR(j,1,6) cout<
//        cout<
//    }
    printf("A->B:%lld\n",dp[n][1]);
    printf("A->C:%lld\n",dp[n][2]);
    printf("B->A:%lld\n",dp[n][3]);
    printf("B->C:%lld\n",dp[n][4]);
    printf("C->A:%lld\n",dp[n][5]);
    printf("C->B:%lld\n",dp[n][6]);
    printf("SUM:%lld\n",dp[n][0]);
    return 0;
}

---

J - 牛牛的宝可梦Go

这题我是真的想不到，虽然现在勉强看懂题解了…
首先用Floyd跑最短路 （我现在只会这个了，你们用高级的也行）
然后dp，设dp[ i ]表示前i个点 到达了点i之后的最大值
转移方程：dp[i]=max(dp[i],dp[i-j]+f[i].v); 这样的复杂度为O(k²) 肯定不行
然后有一点我们是知道的，过了n秒人一定可以到达他可以到达的任意点，我们不妨变通一下 n个宝可梦（因为宝可梦的生成时间均不等）我们可以利用这一点 往前循环n次 以O(n*k)的复杂度过这题

坑点：不能让dp初始值太大 最好是-INF 不然f[ i ].v大的时候会影响答案，至于为什么加INF，你不加的话 能保证是从1开始走的吗

#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#define ls k<<1,l,mid
#define rs k<<1|1,mid+1,r
#define mp(x,y) make_pair(x,y)
#define r(x) read(x)
#define rrr(x,y,z) read(x);read(y);read(z)
#define FOR(i,l,r) for(int i=l;i<=r;i++)
using namespace std;
typedef long long LL;
typedef pair<LL,LL> pt;
const int N=1e5+5;
const int M=2e3+5;
const int INF=0x7fffffff;
const int mod=1e9+7;
const double eps=1e-8;
const double pi=acos(-1);
LL n,m;
LL dis[M][M];
LL dp[N];
struct node
{
    int t,p,v;
}f[N];
template<class T>
inline void read(T &x)
{
    char c; x=1;
    while((c=getchar())<'0'||c>'9') if(c=='-') x=-1;
    T res=c-'0';
    while((c=getchar())>='0'&&c<='9') res=res*10+c-'0';
    x*=res;
}
bool cmp(node a,node b)
{
    return a.t<b.t;
}
int main()
{
    r(n); r(m);
    FOR(i,1,n)
    FOR(j,1,n){
        if(i==j) dis[i][i]=0;
        else dis[i][j]=INF;
    }
    FOR(i,1,m){
        int a,b;
        r(a); r(b);
        dis[a][b]=1;
        dis[b][a]=1;
    }
    FOR(k,1,n)
    FOR(i,1,n)
    FOR(j,1,n){
        if(i!=j&&j!=k&&k!=i){
            dis[i][j]=min(dis[i][j],dis[i][k]+dis[k][j]);
        }
    }
    r(m);
    FOR(i,1,m){
        rrr(f[i].t,f[i].p,f[i].v);
    }
    sort(f+1,f+m+1,cmp);
    memset(dp,0,sizeof dp);
    f[0].p=1;
    LL ans=0;
    LL maxx=-1;
    FOR(i,1,m){
        if(i>n){
            maxx=max(maxx,dp[i-n]);
            dp[i]=maxx+f[i].v;
        }
        else dp[i]=-INF;
        FOR(j,1,n){
            if(i-j<0) break;
            if(dis[f[i].p][f[i-j].p]<=f[i].t-f[i-j].t){
                dp[i]=max(dp[i],dp[i-j]+f[i].v);
            }
        }
        ans=max(dp[i],ans);
    }
    cout<<ans<<endl;
    return 0;
}

---

还是七题，ε=(´ο｀*)))唉