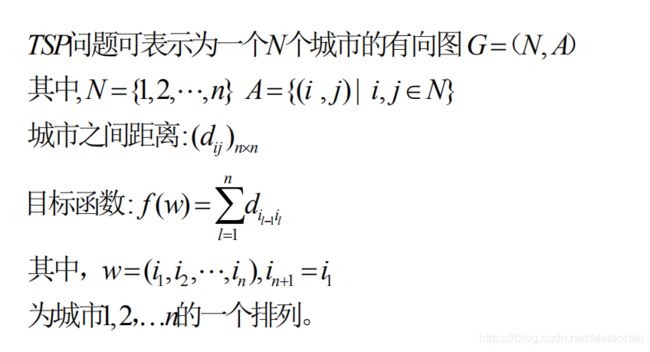Matlab环境下蚁群优化算法关于TSP问题的应用
Matlab环境下蚁群优化算法关于TSP问题的应用
- 1 基本概念
- 1.1生物学原理
- 1.2 基本思想
- 1.3TSP问题
- 2 蚁群算法的基本流程
- 1. 路径构建
- 2. 信息素更新
- 3.流程图
- 3 matlab代码模型展示
- ① 导入城市地图
- ②设置运用到的参数 ★
- ③ 迭代寻找最佳路径
- ④计算城市间的转移概率★
- ⑤轮盘赌决定下一次的旅行城市★
- ⑥ 计算各个蚂蚁的路径距离
- ⑦ 计算最短路径距离及平均距离
- ⑧ 更新信息素和逐个计算
- ⑨ 图形绘制(可视化展示)
- 4 运行结果分析
- 4.1 导入的城市地图设置
- 4.2老师原始参数
- 4.3自设参数
- 4.4最终结论
1 基本概念
蚁群算法是一种用来寻找优化路径的概率型算法。
1.1生物学原理
人们在研究蚂蚁觅食的过程中,发现单个蚂蚁的行为比较简单,但是蚁群整体却可以体现一些智能的行为。例如蚁群可以在不同的环境下,寻找最短到达食物源的路径。这是因为蚁群内的蚂蚁可以通过某种信息机制实现信息的传递。后又经进一步研究发现,蚂蚁会在其经过的路径上释放一种可以称之为“信息素”的物质,蚁群内的蚂蚁对“信息素”具有感知能力,它们会沿着“信息素”浓度较高路径行走,而每只路过的蚂蚁都会在路上留下“信息素”,这就形成一种类似正反馈的机制,这样经过一段时间后,整个蚁群就会沿着最短路径到达食物源了。
1.2 基本思想
将蚁群算法应用于解决优化问题的基本思路为:用蚂蚁的行走路径表示待优化问题的可行解,整个蚂蚁群体的所有路径构成待优化问题的解空间。路径较短的蚂蚁释放的信息素量较多,随着时间的推进,较短的路径上累积的信息素浓度逐渐增高,选择该路径的蚂蚁个数也愈来愈多。最终,整个蚂蚁会在正反馈的作用下集中到最佳的路径上,此时对应的便是待优化问题的最优解。
1.3TSP问题
在求解这个问题前,我们先来回顾以下tsp问题的定义。旅行商问题,即TSP问题(Travelling Salesman Problem)又译为旅行推销员问题、货郎担问题,是数学领域中著名问题之一。假设有一个旅行商人要拜访n个城市,他必须选择所要走的路径,路径的限制是每个城市只能拜访一次,而且最后要回到原来出发的城市。路径的选择目标是要求得的路径路程为所有路径之中的最小值。
2 蚁群算法的基本流程
蚁群AS算法对TSP问题的求解主要有两大步骤:
1. 路径构建
2. 信息素更新
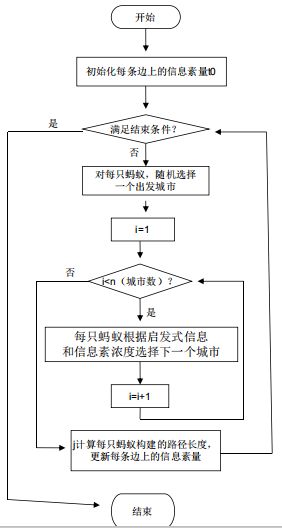
3.流程图
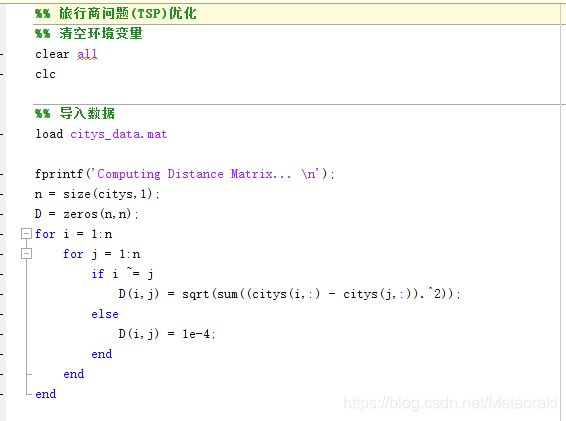
3 matlab代码模型展示
① 导入城市地图
设置好多个城市构建路径,将设计好的城市地图(一般为有向图)导入matlab环境模型中。
②设置运用到的参数 ★
其中非常重要影响迭代能力,进而求出最后的最佳路径的主要参数为:
alpha α :信息素重要程度因子
beta β :启发函数重要程度因子(一般为距离的倒数,这里的距离一 般采用欧几里得距离求解)
rho ρ : 信息素挥发因子
重要程度是指对影响蚂蚁选择下一次的旅行城市的概率的影响因素所占的概率,图中所示基础的第一次运行表示启发函数的重要程度较高。

③ 迭代寻找最佳路径
这边比较重要的变量为禁忌表,用于存放已经走过的城市,不重复旅行。

④计算城市间的转移概率★
⑤轮盘赌决定下一次的旅行城市★
⑥ 计算各个蚂蚁的路径距离
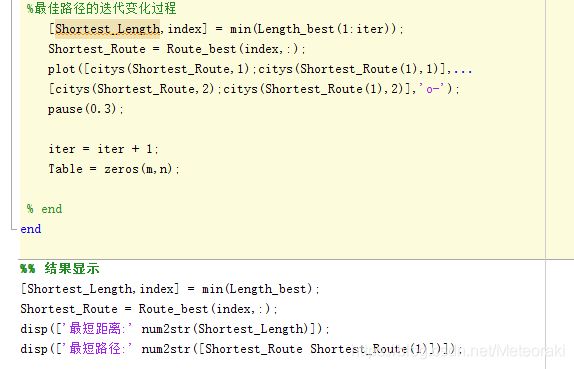
⑦ 计算最短路径距离及平均距离
通过不断的迭代,可以通过这两个变量看出α,β,ρ三个参数对迭代效率的影响。

⑧ 更新信息素和逐个计算
迭代次数+1,清空原来路径记录,开始下一轮新的迭代。
⑨ 图形绘制(可视化展示)
4 运行结果分析
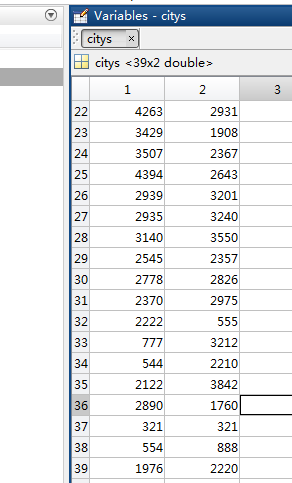
4.1 导入的城市地图设置
如下图所示:
大概设置了39座城市作为此次的TSP问题的地图组成。
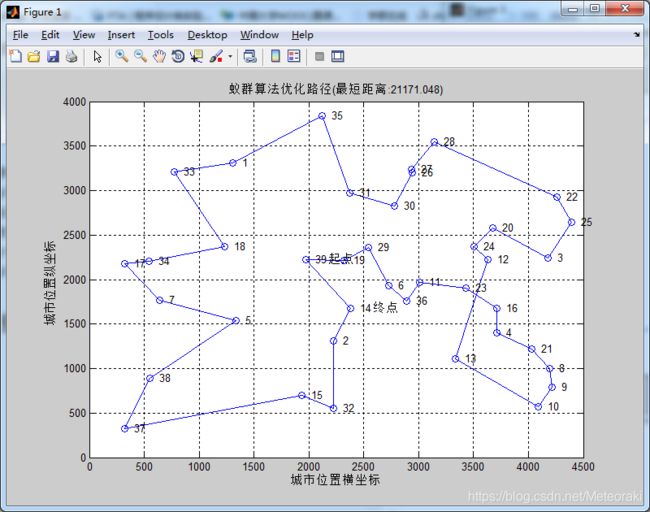
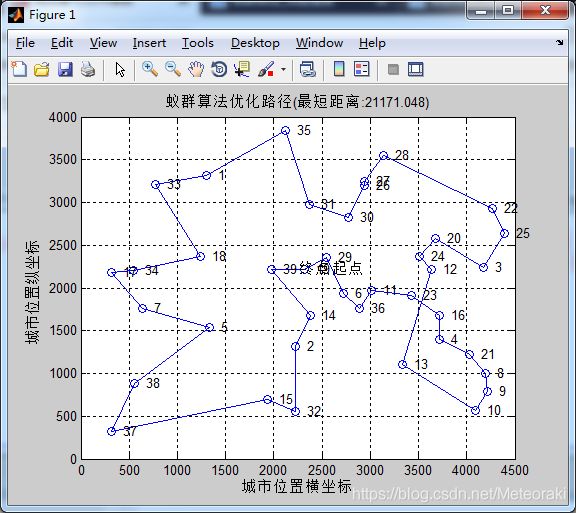
4.2老师原始参数
α=1 β=5 ρ= 0.1
从图中可以看出求出的最短距离为21171
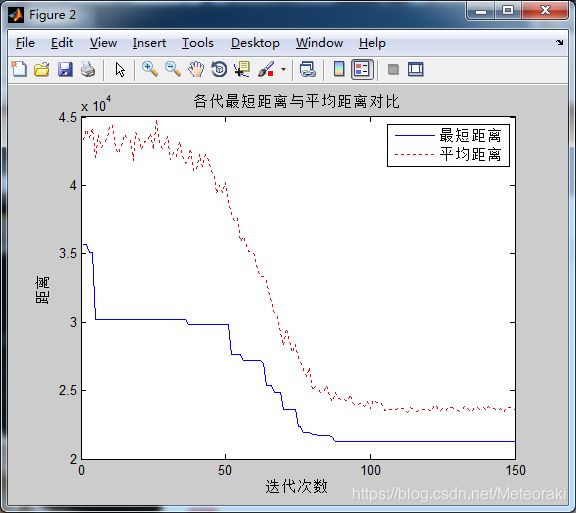
在迭代过程中,最短距离变换平缓,且不断发生变化,最后趋于平稳。
(在这里启发函数的重要程度较大)
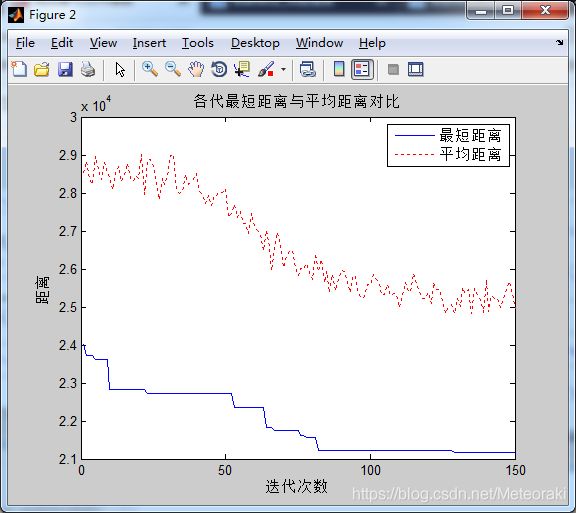
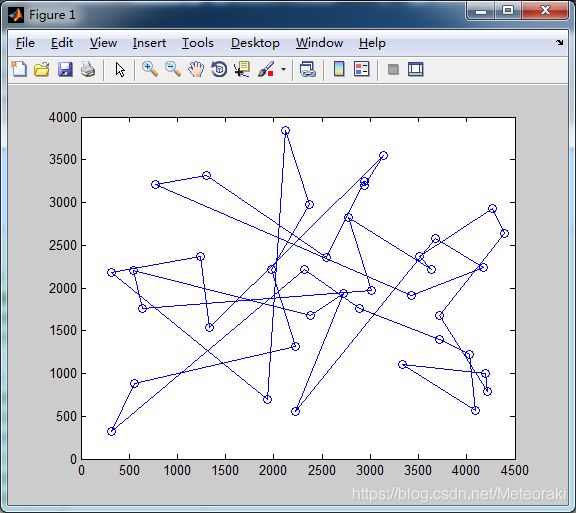
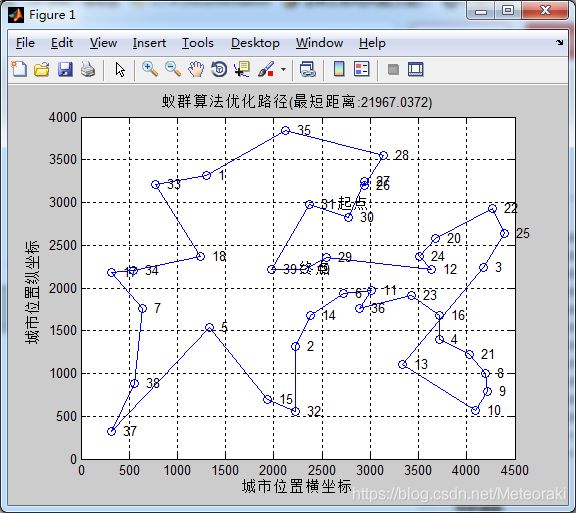
4.3自设参数
α=10 β=1 ρ= 0.1
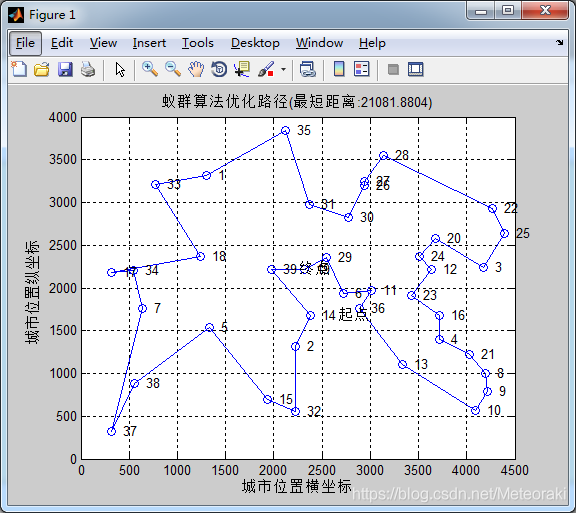
从图中可以看出求出的最短距离为21081
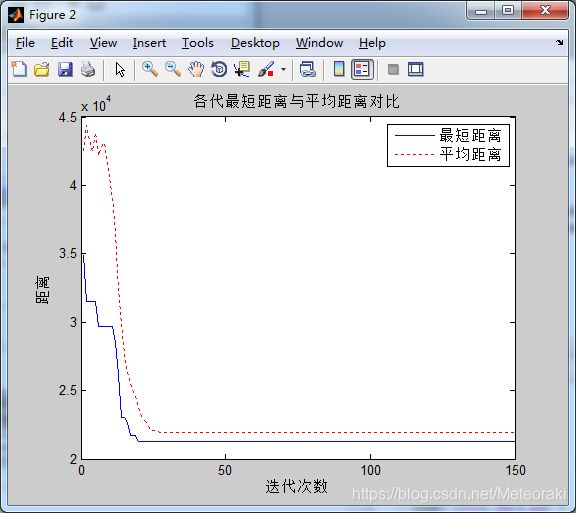
开始迭代以后,刚开始蚁群的迭代十分混乱,因为迭代侧重于信息素,前期一团乱麻,蚁群活动较为随机,后来随着蚁群的生物特性,最短距离骤降,很快趋于平稳。
刚开始的路线可以从图上看出十分混乱。
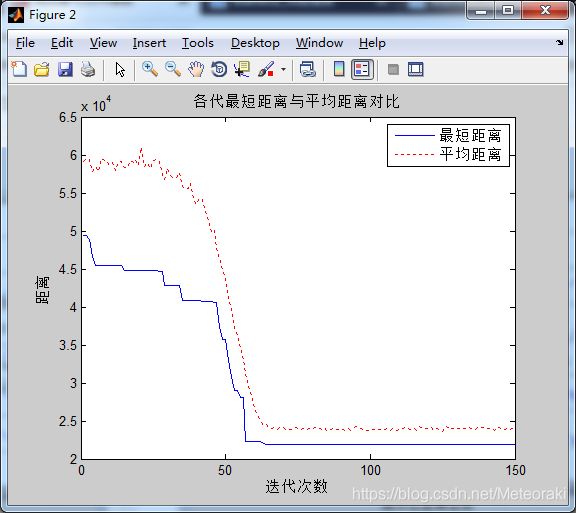
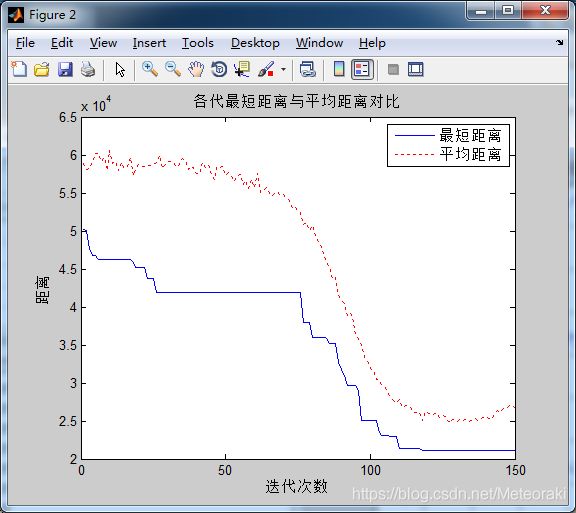
α=10 β=1 ρ= 0.05
从图中可以看出求出的最短距离为21081
与上一条测试来看,不同的地方为信息素的挥发速度减缓了,即蚁群的学习能力和受信息素的影响时间拉长,即虽然最短距离有骤降但是总体的没有之前的快速。
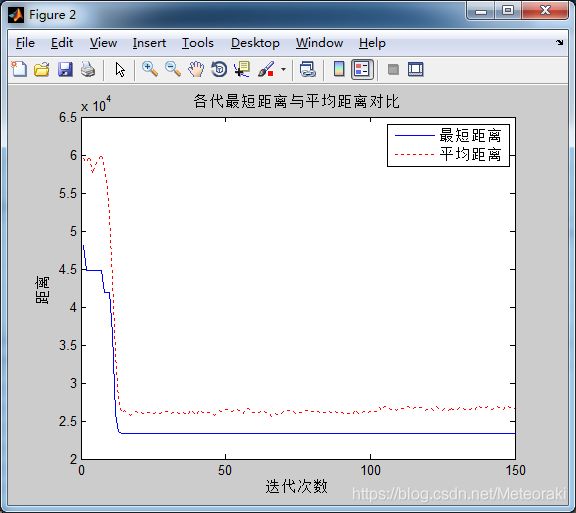
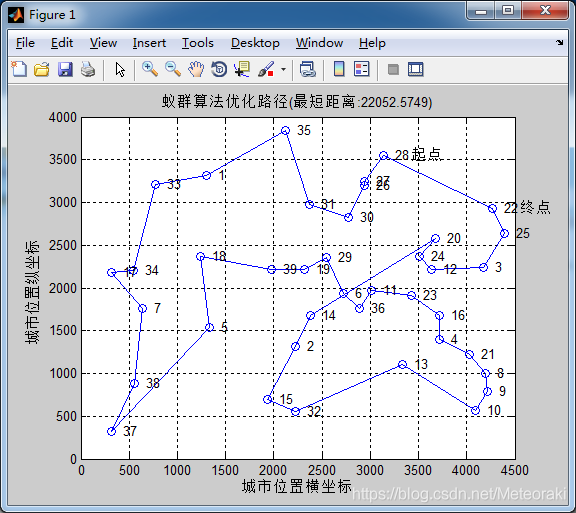
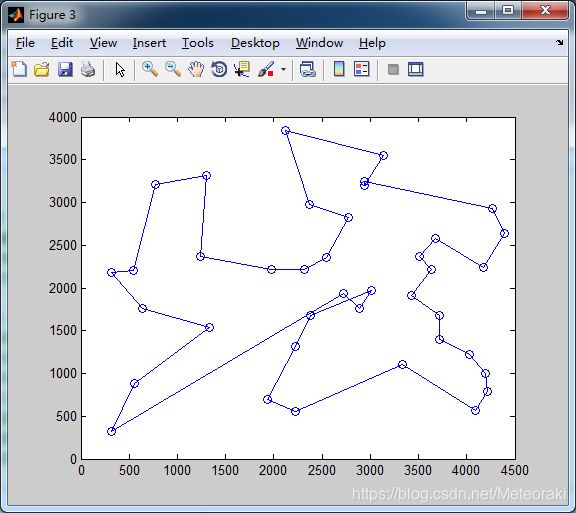
α=10 β=2 ρ= 0.5
从图中可以看出求出的最短距离为22052
与上一条测试来看,不同的使这次我们提高了蚁群的信息素挥发速度,可以看出骤降速度极快,且后期的迭代基本不再发生变化,即很快就能得出该参属下的最短距离。也正是因为信息素挥发过快,且占比大,所有其得到的最短距离相较于其他没有那么小。(信息素的重要因子和信息素的挥发相互影响)
 a=2 b=2 r=0.1
a=2 b=2 r=0.1
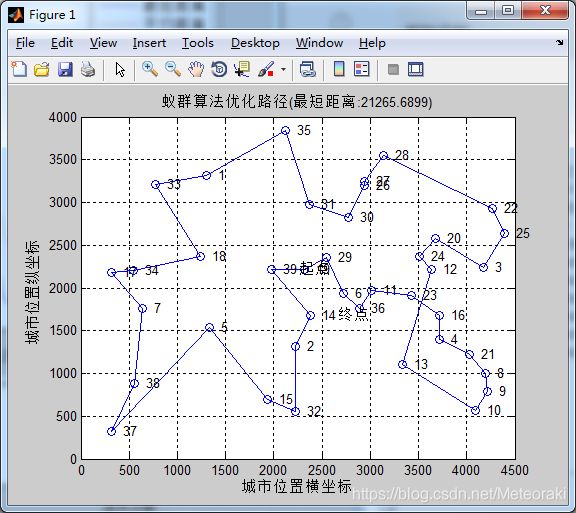
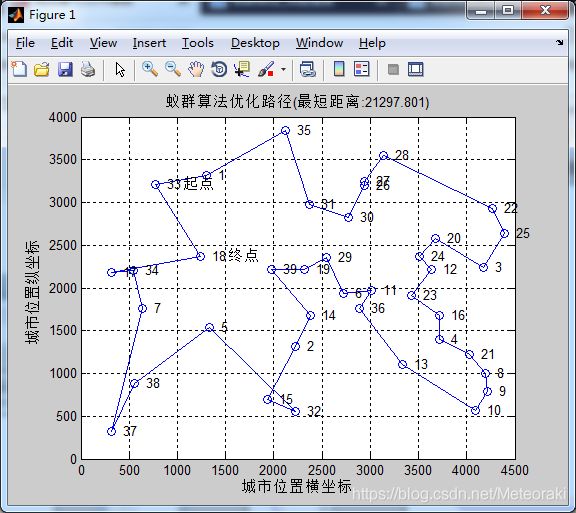
α=2 β=2 ρ= 0.1
从图中可以看出求出的最短距离为21265
即二者的影响因素相等,挥发速度也持普通速度
最短距离的求取也变得平庸了
 a=2 b=10,r=0.1
a=2 b=10,r=0.1
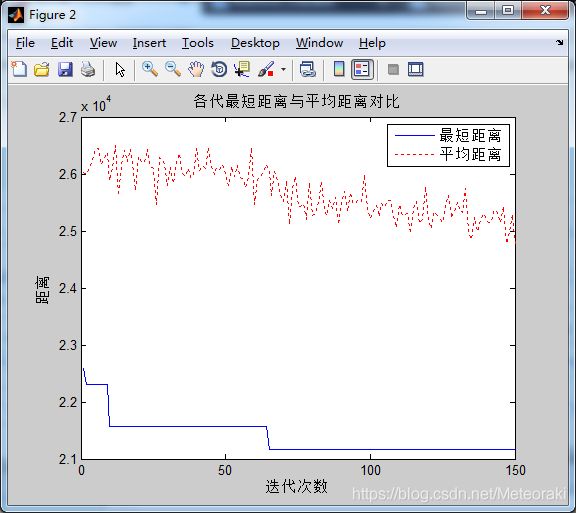
α=2 β=10 ρ= 0.1
从图中可以看出求出的最短距离为21171
从图中可以看出迭代变换缓慢,启发函数占比越大,则越快能达到迭代的最后结果,但是可以看出其最短距离的求解并没有最优。
4.4最终结论
所以信息素取较大重要因子,配合不宜太容易挥发的信息素和启发函数,能够得到较为优化的解,但是迭代次数相较于启发函数占主导,所需要的迭代次数会更大一些。