树与二叉树

本文主要整理数据结构中和树相关的重要或较难的知识点，仅供个人复习。

二叉树的主要性质

1）非空二叉树上叶子节点数等于双分支节点数+1。
2）二叉树的第 i 层上最多有 $2^{i-1}(i>=1)$ 个节点。
3）高度（深度）为 k 的二叉树最多有 $2^k-1(k>=1)$ 个节点。
4）有 n 个节点的完全二叉树，对各个节点从上到下、从左到右依次编号（1~n），节点之间有如下关系：

• 编号为 x 的节点的父亲编号是 $\lfloor \frac{x}{2}\rfloor$；
• 编号为 x 的节点的左儿子编号是 2x，右儿子编号为 2x+1。

5）Catalan()：给定 n 个节点，能构成 Catalan( n ) 中不同的二叉树。
6）具有 n 个节点的完全二叉树的深度（高度）为 $\lfloor lo{g}_{2}n+1\rfloor$。

以上性质均可以通过画一个结构简单的树得到。

二叉树的非递归遍历

线索二叉树

通过二叉链表来构造二叉树，其中空闲的指针域总是过半，因此提出了一种利用空链表域放指针，指向其它节点的思路，称这种指针为线索。

如果树上有 n 个节点，那么就会有 2n 个指针域，而树上是只有 n - 1 条边的，因此我们只用了 n-1 个指针域，浪费了 n+1 个；故一棵有 n 个节点的线索二叉树共有 n+1 个线索。

记 ptr 指向二叉链表中的一个结点，以下是建立线索的规则：

1. 如果 ptr->lchild 为空，则存放指向中序遍历序列中该结点的前驱结点。这个结点称为 ptr 的中序前驱；
2. 如果 ptr->rchild 为空，则存放指向中序遍历序列中该结点的后继结点。这个结点称为 ptr 的中序后继；

显然，在决定 lchild 是指向左孩子还是前驱，rchild 是指向右孩子还是后继，需要一个区分标志的。因此，我们在每个结点再增设两个标志域 ltag 和 rtag，注意 ltag 和 rtag 只是区分 0 或 1 数字的布尔型变量，其占用内存空间要小于像 lchild 和 rchild 的指针变量。结点结构如下所示。
| lchild | ltag | rchild | rtag |
注意： ltag = 0 表示 lchild 指向左孩子，ltag = 1 表示 lchild 为线索，虽然反过来定义也可以，但是考研教材就这样默认的。

线索化的实质就是将二叉链表中的空指针改为指向前驱或后继的线索。由于前驱和后继信息只有在遍历该二叉树时才能得到，所以，线索化的过程就是在遍历的过程中修改空指针的过程。

二叉树的前驱与后继

由于线索二叉树中的线索是指向前驱和后继，因此这里要介绍前驱后继定义及求法。
这里只介绍中序遍历下的前驱与后继，其它遍历的定义类似。

节点 x 的前驱就是遍历中在 x 之前的、最后一个被访问的节点。 依据定义，x 中序遍历下的前驱也就是中序遍历序列中 x 前面的节点。
类似的，节点 x 的后继就是遍历中在 z 之后被访问的第一个节点。

于是这就为我们画线索树提供了指导。在中序遍历下，x 的前驱就是其左子树上最后一个被访问的节点，即最右边的节点；后继就是其右子树第一个被访问的节点，即右子树上最左边的节点。

注： 以上所说的“访问”是指读取数据，路过不算；我们知道中序遍历是先遍历当前节点的左子树才访问它。

怎么使用线索二叉树，怎么用代码实现线索二叉树不写了。

树与二叉树的转换

树转二叉树

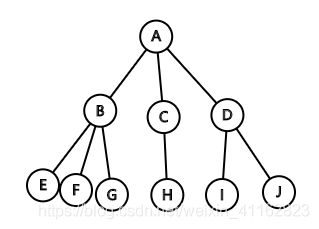
树转二叉树遵循左儿子右兄弟的规律。以图1为例，节点 A 有 3 个儿子 B C D ，而 C 和 D 是 B 的兄弟。所谓的“左儿子右兄弟”即转化后的二叉树的左子节点是自己的儿子，右子节点上全是自己的兄弟。

如果这样操作，得到如图 3 所示的二叉树，那么原树中的结构信息是否会被破坏呢？显然不会，因为儿子的兄弟是儿子，兄弟的兄弟是兄弟，所以可以根据这个关系还原原树上一个节点的所有儿子。

具体的，根据上述转换理论会有如下结论：

1. 二叉树的左右儿子有区别，不可互换；
2. 二叉树上当前节点的左子节点是儿子，右子节点是兄弟（在原树上）；
3. 兄弟的兄弟还是兄弟；
4. 儿子的兄弟还是儿子。

上述结论正确性显而易见，完全是根据转换定义得出来的结论。至此我们证明了“左儿子右兄弟”思路的正确性与实用性，下面就是具体操作步骤。

1. 加线：就是在所有兄弟结点之间加一条连线；
2. 抹线：就是对树中的每个结点，只保留他与第一个孩子结点之间的连线，删除它与其它孩子结点之间的连线；
3. 旋转：就是以树的根结点为轴心，将整棵树顺时针旋转一定角度，使之结构层次分明。

以上 3 个步骤分别对应图 1 2 3 。

图1：普通树

图2：进行左儿子右兄弟后的二叉树

图3：旋转调整后的最终二叉树

二叉树转树

根据上述结论 3 和 4，二叉树上某个节点 X 的左节点是 X 在原树上的儿子，左节点的右子节点是 X 儿子的兄弟，也是Ｘ的儿子，同理，左节点的右节点的右节点还是 X 的儿子，… ；例如图 3 中，E 为 B （在原树中，下同）的儿子，F 为 E 的兄弟，故 F 也是 B 的儿子，而 G 是 F 的兄弟，故 G 也是 E 的兄弟，故 G 也是 B 的儿子。

顺着这个关系我们就可以还原原树的（完整）结构。上述步骤其实也就是二叉树转树的核心思想及其步骤。

具体的步骤可以描述如下：

1. 若某结点的左孩子结点存在，将左孩子结点，左孩子节点的右孩子结点、右孩子结点的右孩子结点 … 都作为该结点的孩子结点，将该结点与这些右孩子结点用线连接起来；
2. 删除原二叉树中所有结点与其右孩子结点的连线；
3. 整理 1 和 2 两步得到的树，使之结构层次分明。

森林转二叉树

森林也不过是若干棵树而已，因此可以先把每颗树都按照上述步骤转化为二叉树，又由于转化后的二叉树根节点是没有右儿子的（因为根节点没有兄弟），因此可以利用这个把所有二叉树依次连接到上一个二叉树的右儿子节点位置，就形成了一颗根节点有右儿子的二叉树。

具体步骤如下：

1. 先把每棵树转换为二叉树；
2. 第一棵二叉树不动，从第二棵二叉树开始，依次把后一棵二叉树的根结点作为前一棵二叉树的根结点的右孩子结点，用线连接起来。当所有的二叉树连接起来后得到的二叉树就是由森林转换得到的二叉树。

二叉树转森林

二叉树转换为森林比较简单，其步骤如下：

1. 先把每个结点与右孩子结点的连线删除，得到分离的二叉树；
2. 把分离后的每棵二叉树转换为树；
3. 整理第 2 步得到的树，使之规范，得到森林。

以上就是二叉树与树和森林之间的转换步骤，上述步骤既适合手工模拟，也适合代码实现。

根据遍历序列建树

已知二叉树的两种遍历序列，来求另一种遍历。这类题目如果仅仅是求另一个序列的内容的话有两种方法，一种是直接利用先序/后序遍历的特点来找当前树的根节点，然后再通过中序遍历划分子树，递归求解，由于一般是选择题，序列不会太长，因此计算不会太复杂。另一种方式是先建树再求目标序列。

已知先序遍历和中序遍历，求后序遍历

解题思路
由先序遍历的特点可知，先序遍历第一个元素为二叉树的根。由中序遍历的特点可知，二叉树的根的左面为左子树的中序遍历，右面为右子树的中序遍历。

由先序遍历可以知道二叉树的根，由中序遍历可以知道二叉树的左子树和右子树，因此，我们可以用递归的思想，将整个二叉树递归分解成左子树和右子树，直到子树为空为止。

实现细节
已知先序遍历是先遍历当前二叉树的根，然后递归遍历左子树和右子树。再由中序遍历根的位置可以得出左子树和右子树的长度（大小）。再将左右子树的长度带入先序遍历，就可以得出左子树的先序遍历和右子树的先序遍历，结合左右子树的中序遍历，就可以递归求解。

已知后序遍历和中序遍历，求先序遍历

解题思路
总体思想和用先序、中序求后序相同。后序遍历是先遍历左右子树，最后才是根。因此，后序遍历最后一个元素是二叉树的根。在中序遍历找到根的位置，根的左面就是左子树的中序遍历，右边就是右子树的先序遍历，根据其长度，将后序遍历分成左右子树的后序遍历。

实现细节
假设中序遍历中，根的左面有lenA个元素，右边有lenB个元素，那么就可以知道其左子树有lenA个元素，右子树有lenB个子树。由后序遍历的特点可知，最后一个元素为根，根的前面lenB个元素为右子树的后序遍历，在这些元素前面的lenA个元素为左子树的后序遍历，因此可以递归求解。

代码示例
下述代码将会读入一棵树的后序遍历和中序遍历，构造好该树后会输出它的先序遍历。

#include
using namespace std;
const int maxn = 50;
char post[maxn],in[maxn];
struct Node{
	char data;
	Node *ls,*rs;
};
Node* BuildTree(Node *root,int l1,int r1,int l2,int r2){
	if(l1 > r1)	return NULL;
	root = new Node();
	root->data = post[r1];
	int p = l2;
	while(in[p] != post[r1])	p++;
	int len = p-l2;
	root->ls = BuildTree(root->ls,l1,l1+len-1,l2,l2+len-1);
	root->rs = BuildTree(root->rs,l1+len,r1-1,l2+len+1,r2);
	return root;
}
void printTree(Node *root){
    cout << root->data << " ";
	if(root->ls != NULL)	printTree(root->ls);
	if(root->rs != NULL)	printTree(root->rs);
	return;
}
int main(){
	int n;
    freopen("in","r",stdin);
    freopen("out","w",stdout);
	scanf("%d",&n);
	scanf("%s%s",post,in);
	Node* root;
	root = BuildTree(root,0,n-1,0,n-1);
    printTree(root);
	return 0;
}

一个测试用例：

8
AEFDHZMG
ADEFGHMZ