PyTorch 不同类型的优化器
不同类型的优化器
- 随机梯度下降法(SGD)
如果我们的样本非常大,比如数百万到数亿,那么计算量异常巨大。因此,实用的算法是SGD算法。在SGD算法中,每次更新的迭代,只计算一个样本。这样对于一个具有数百万样本的训练数据,完成一次遍历就会对更新数百万次,效率大大提升。由于样本的噪音和随机性,每次更新并不一定按照减少的方向。
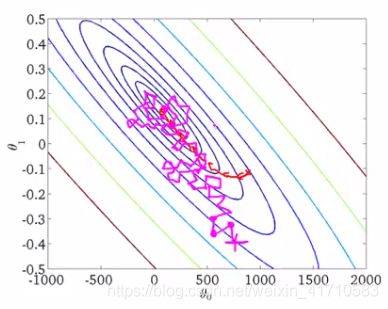
如上图,椭圆表示的是函数值的等高线,椭圆中心是函数的最小值点。红色是BGD的逼近曲线,而紫色是SGD的逼近曲线。我们可以看到BGD(批量梯度下降算法)是一直向着最低点前进的,而SGD明显躁动了许多,但总体上仍然是向最低点逼近的。
最后需要说明的是,SGD不仅仅效率高,而且随机性有时候反而是好事。今天的目标函数是一个『凸函数』,沿着梯度反方向就能找到全局唯一的最小值。然而对于非凸函数来说,存在许多局部最小值。随机性有助于我们逃离某些很糟糕的局部最小值,从而获得一个更好的模型。
代码可以参考上一节
- 动量法(Momentum)
如果把梯度下降法想象成一个小球从山坡到山谷的过程,那么前面几篇文章的小球是这样移动的:从A点开始,计算当前A点的坡度,沿着坡度最大的方向走一段路,停下到B。在B点再看一看周围坡度最大的地方,沿着这个坡度方向走一段路,再停下。确切的来说,这并不像一个球,更像是一个正在下山的盲人,每走一步都要停下来,用拐杖来来探探四周的路,再走一步停下来,周而复始,直到走到山谷。而一个真正的小球要比这聪明多了,从A点滚动到B点的时候,小球带有一定的初速度,在当前初速度下继续加速下降,小球会越滚越快,更快的奔向谷底。momentum 动量法就是模拟这一过程来加速神经网络的优化的。

在CNN的训练中,我们的开山祖师已经给了我们冲量的建议配置——0.9(刚才的例子全部是0.7),那么0.9的冲量有多大量呢?终于要来点公式了……
我们用G表示每一轮的更新量,g表示当前一步的梯度量(方向*步长),t表示迭代轮数,\gamma表示冲量的衰减程度,那么对于时刻t的梯度更新量有:
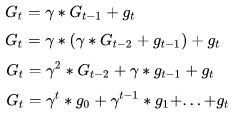
那么我们可以计算下对于梯度g0对从G0到GT的总贡献量为
![]()
- 对应实现代码
#定义函数二元二次函数z=x^2+50y^2
def f(x):
return x[0] * x[0] + 50 * x[1] * x[1]
def g(x):
return np.array([2 * x[0], 100 * x[1]])
xi = np.linspace(-200,200,1000)
yi = np.linspace(-100,100,1000)
X,Y = np.meshgrid(xi, yi)
Z = X * X + 50 * Y * Y
#momentum算法
def momentum(x_start, step, g, discount=0.7): # gd代表了Gradient Descent
x = np.array(x_start, dtype='float64')
passing_dot = [x.copy()]
pre_grad = np.zeros_like(x)
for i in range(50):
grad = g(x)
pre_grad = pre_grad * discount + grad
x -= pre_grad * step
passing_dot.append(x.copy())
print(
'[ Epoch {0} ] grad = {1}, x = {2}'.format(i, grad, x))
if abs(sum(grad)) < 1e-6:
break;
return x, passing_dot
- 结果
grad表示对应x和y的梯度,x为上次和本次的变化范围
[ Epoch 38 ] grad = [-0.26399377 0.4346231 ], x = [-0.13411544 -0.09018577]
[ Epoch 39 ] grad = [-0.26823088 -9.01857721], x = [-0.13130674 -0.01206094]
[ Epoch 40 ] grad = [-0.26261348 -1.20609389], x = [-0.12513883 0.06192395]
[ Epoch 41 ] grad = [-0.25027766 6.19239466], x = [-0.11681685 0.01463505]
[ Epoch 42 ] grad = [-0.2336337 1.46350519], x = [-0.10725333 -0.04188326]
[ Epoch 43 ] grad = [-0.21450666 -4.18832574], x = [-0.09712675 -0.01443286]
[ Epoch 44 ] grad = [-0.19425351 -1.44328621], x = [-0.0869301 0.02787499]
[ Epoch 45 ] grad = [-0.17386019 2.7874994 ], x = [-0.07701067 0.0128905 ]
[ Epoch 46 ] grad = [-0.15402135 1.28905028], x = [-0.06760274 -0.01822345]
[ Epoch 47 ] grad = [-0.13520547 -1.82234455], x = [-0.05885389 -0.0108457 ]
[ Epoch 48 ] grad = [-0.11770778 -1.08456965], x = [-0.05084638 0.01167184]
[ Epoch 49 ] grad = [-0.10169275 1.16718422], x = [-0.04361403 0.00875917]
adagrad
前面的一系列文章的优化算法有一个共同的特点,就是对于每一个参数都用相同的学习率进行更新。但是在实际应用中各个参数的重要性肯定是不一样的,所以我们对于不同的参数要动态的采取不同的学习率,让目标函数更快的收敛。
adagrad方法是将每一个参数的每一次迭代的梯度取平方累加再开方,用基础学习率除以这个数,来做学习率的动态更新。这个比较简单,直接上公式。
RMSProp
import d2lzh as d2l
import math
from mxnet import nd
def rmsprop_2d(x1, x2, s1, s2):
g1, g2, eps = 0.2 * x1, 4 * x2, 1e-6
s1 = gamma * s1 + (1 - gamma) * g1 ** 2
s2 = gamma * s2 + (1 - gamma) * g2 ** 2
x1 -= eta / math.sqrt(s1 + eps) * g1
x2 -= eta / math.sqrt(s2 + eps) * g2
return x1, x2, s1, s2
def f_2d(x1, x2):
return 0.1 * x1 ** 2 + 2 * x2 ** 2
eta, gamma = 0.4, 0.9
d2l.show_trace_2d(f_2d, d2l.train_2d(rmsprop_2d))
#结果
epoch 20, x1 -0.010599, x2 0.000000
Adam
- 介绍
https://blog.csdn.net/leadai/article/details/79178787 深度学习最常用的学习算法:Adam优化算法 - 代码
import torch
# N is batch size; D_in is input dimension;
# H is hidden dimension; D_out is output dimension.
N, D_in, H, D_out = 64, 1000, 100, 10
# Create random Tensors to hold inputs and outputs
x = torch.randn(N, D_in)
y = torch.randn(N, D_out)
# Use the nn package to define our model and loss function.
model = torch.nn.Sequential(
torch.nn.Linear(D_in, H),
torch.nn.ReLU(),
torch.nn.Linear(H, D_out),
)
loss_fn = torch.nn.MSELoss(reduction='sum')
# Use the optim package to define an Optimizer that will update the weights of
# the model for us. Here we will use Adam; the optim package contains many other
# optimization algoriths. The first argument to the Adam constructor tells the
# optimizer which Tensors it should update.
learning_rate = 1e-4
optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate)
for t in range(500):
# Forward pass: compute predicted y by passing x to the model.
y_pred = model(x)
# Compute and print loss.
loss = loss_fn(y_pred, y)
print(t, loss.item())
# Before the backward pass, use the optimizer object to zero all of the
# gradients for the variables it will update (which are the learnable
# weights of the model). This is because by default, gradients are
# accumulated in buffers( i.e, not overwritten) whenever .backward()
# is called. Checkout docs of torch.autograd.backward for more details.
optimizer.zero_grad()
# Backward pass: compute gradient of the loss with respect to model
# parameters
loss.backward()
# Calling the step function on an Optimizer makes an update to its
# parameters
optimizer.step()
- 结果
为迭代次数以及对应的损失
488 2.2479953543097508e-07
489 2.130966834101855e-07
490 2.0217059670812887e-07
491 1.917220657787766e-07
492 1.8173946614297165e-07
493 1.7244451555598062e-07
494 1.635135902233742e-07
495 1.5510966022702632e-07
496 1.4692679428662814e-07
497 1.3925993869179365e-07
498 1.3208712346113316e-07
499 1.25094473446552e-07
参考文章
https://blog.csdn.net/tsyccnh/article/details/76769232 深度学习优化函数详解
https://www.zybuluo.com/hanbingtao/note/448086 零基础入门深度学习(2) - 线性单元和梯度下降

