从梯度下降到反向传播
从梯度下降到反向传播
- 1 梯度下降
- 1.1 偏微分
- 1.2 梯度下降
- 2 反向传播
- 2.1 矩阵乘法求导
- 2.1.1 数学中的乘法($.$)求导
- 2.1.2 numpy中的默认乘法,对应位置相乘 ($\cdot *$) 求导
- 2.2 反向传播算法
- 2.2.1 求每一层的误差 $\delta$
- 2.2.2 求每一层权重的偏导数 $\partial J\over\partial \theta^{(i)}$
- 2.2.3 反向传播算法总结
- 3 梯度爆炸和梯度消失
- 3.1 梯度爆炸消失对反向传播的影响
- 3.2 梯度爆炸消失对前馈网络的影响
- 3.3 梯度爆炸、梯度消失原因总结
本文的思路如下:
偏微分 -> 梯度下降 -> 矩阵求导 -> 反向传播
1 梯度下降
1.1 偏微分
下图是一个 z = cos ( x ) + sin ( y ) z=\cos(x)+\sin(y) z=cos(x)+sin(y) 的函数图像,假设有一个点 p 1 ( x 1 , y 1 ) p_1(x_1, y_1) p1(x1,y1),求在p1点处关于x的偏微分 ∂ z ∂ x ∣ x = x 1 {\partial z\over \partial x}|_{x=x_1} ∂x∂z∣x=x1 的思路如下:
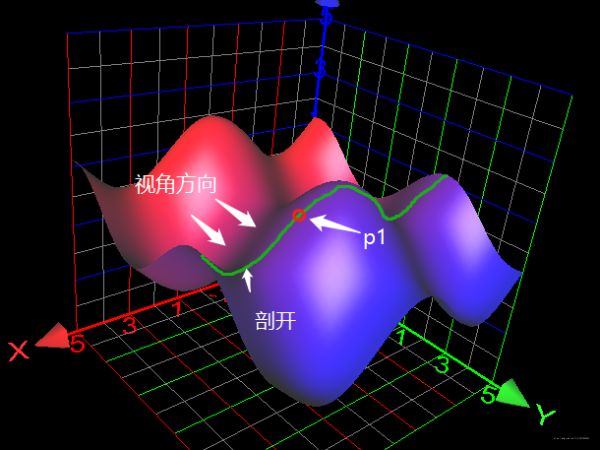
- 取一个平行于 x ⃗ 、 z ⃗ \vec{x}、\vec{z} x、z的平面a要求这个平面过p1,与函数相交于上图中的绿色曲线
- 画出平面a的正视图,视角沿着上图中的视角箭头,得到下图(注意坐标值)。
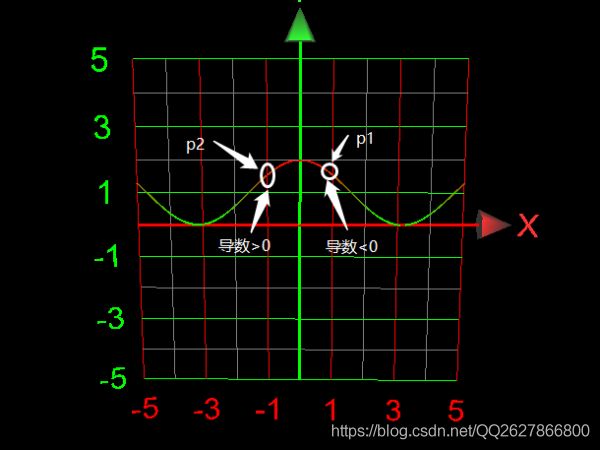
- 在上述图像中求解曲线在p1点处的导数,即我们要求的 ∂ z ∂ x ∣ x = x 1 {\partial z\over\partial x}|_{x={x_1}} ∂x∂z∣x=x1
通过图投影图,在p1处的导数<0;在p2处的导数>0。从而:
- 沿着x增大的方向,下坡方向,那么导数<0;如果要到达谷底,需要 x − α ∂ z ∂ x x-\alpha{\partial z\over\partial x} x−α∂x∂z
- 沿着x增大的方向,上坡方向,那么导数>0;如果要到达谷底,需要 x − α ∂ z ∂ x x-\alpha{\partial z\over\partial x} x−α∂x∂z
即:无论在哪里,偏导数值相反方向,都是到达谷底的方向。
其中 α \alpha α 应为一个小数,偏导数只是指明了谷底的方向,但是要是迈步过大,容易直接跨过谷底到达另一个山坡位置
1.2 梯度下降
总结偏微分的原理,得到梯度下降公式如下:
θ i = θ i − α ∂ J ( θ 0 , ⋯ , θ n ) ∂ θ i , f o r i = 0 t o n \theta_i = \theta_i -\alpha{\partial J(\theta_0,\cdots,\theta_n)\over \partial\theta_i}, for\ i=0\ to\ n θi=θi−α∂θi∂J(θ0,⋯,θn),for i=0 to n
其中 α \alpha α 控制步伐大小,不断重复上述更新,直到拟合,即到达下图的山谷位置,过程如下图所示:
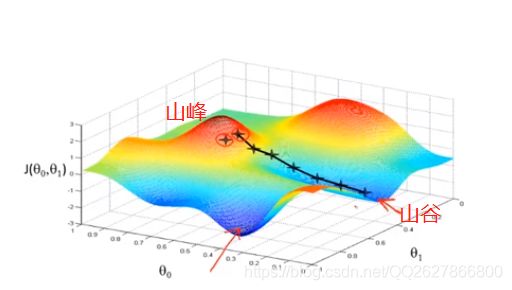
即:梯度更新的算法核心在于求目标函数关于变量 θ \theta θ 偏微分
2 反向传播
2.1 矩阵乘法求导
常见的矩阵乘法有两种,一种是数学上的乘法,另一种是对应位置相乘,例如:
- 数学上的乘法,这里我们记为 ⋅ \cdot ⋅ ,例如:
[ a 11 a 12 a 21 a 22 ] ⋅ [ b 11 b 12 b 21 b 22 ] = [ a 11 b 11 + a 12 b 21 a 11 b 12 + a 12 b 22 a 21 b 11 + a 22 b 21 a 21 b 12 + a 22 b 22 ] \begin{bmatrix} a_{11}&a_{12}\\ a_{21}&a_{22}\\ \end{bmatrix}\cdot\begin{bmatrix} b_{11}&b_{12}\\ b_{21}&b_{22}\\ \end{bmatrix}=\begin{bmatrix} a_{11}b_{11}+a_{12}b_{21}&a_{11}b_{12}+a_{12}b_{22}\\ a_{21}b_{11}+a_{22}b_{21}&a_{21}b_{12}+a_{22}b_{22}\\ \end{bmatrix}\\ [a11a21a12a22]⋅[b11b21b12b22]=[a11b11+a12b21a21b11+a22b21a11b12+a12b22a21b12+a22b22]
- numpy中的默认乘法,为对应位置相乘,这里我们记为 ⋅ ∗ \cdot * ⋅∗ ,例如:
[ a 11 a 12 a 21 a 22 ] ⋅ ∗ [ b 11 b 12 b 21 b 22 ] = [ a 11 b 11 a 12 b 12 a 21 b 21 a 22 b 22 ] \begin{bmatrix} a_{11}&a_{12}\\ a_{21}&a_{22}\\ \end{bmatrix}\cdot*\begin{bmatrix} b_{11}&b_{12}\\ b_{21}&b_{22}\\ \end{bmatrix}=\begin{bmatrix} a_{11}b_{11}&a_{12}b_{12}\\ a_{21}b_{21}&a_{22}b_{22}\\ \end{bmatrix}\\ [a11a21a12a22]⋅∗[b11b21b12b22]=[a11b11a21b21a12b12a22b22]
2.1.1 数学中的乘法( . . .)求导
假设有如下计算矩阵:
[ x 11 x 12 x 21 x 22 x 31 x 32 ] ⋅ [ a 11 a 12 a 13 a 21 a 22 a 23 ] = [ z 11 z 12 z 13 z 21 z 22 z 23 z 31 z 32 z 33 ] \begin{bmatrix} x_{11}&x_{12}\\ x_{21}&x_{22}\\ x_{31}&x_{32}\\ \end{bmatrix}\cdot\begin{bmatrix} a_{11}&a_{12}&a_{13}\\ a_{21}&a_{22}&a_{23}\\ \end{bmatrix}=\begin{bmatrix} z_{11}&z_{12}&z_{13}\\ z_{21}&z_{22}&z_{23}\\ z_{31}&z_{32}&z_{33}\\ \end{bmatrix}\\ ⎣⎡x11x21x31x12x22x32⎦⎤⋅[a11a21a12a22a13a23]=⎣⎡z11z21z31z12z22z32z13z23z33⎦⎤
且上述运算只是链式计算中的一环,即有 J = f ( Z ) J=f(Z) J=f(Z) ,如果对z矩阵的每个元素求偏导,那么组合起来的矩阵一定是和z矩阵一样,即有:
∂ J ∂ Z = Δ = [ δ 11 δ 12 δ 13 δ 21 δ 22 δ 23 δ 31 δ 32 δ 33 ] {\partial J\over\partial Z}=\Delta=\begin{bmatrix} \delta_{11}&\delta_{12}&\delta_{13}\\ \delta_{21}&\delta_{22}&\delta_{23}\\ \delta_{31}&\delta_{32}&\delta_{33}\\ \end{bmatrix}\\ ∂Z∂J=Δ=⎣⎡δ11δ21δ31δ12δ22δ32δ13δ23δ33⎦⎤
在此基础上求解: ∂ J ∂ X \partial J\over\partial X ∂X∂J
由于:
x 11 a 11 + x 12 a 21 = z 11 x 11 a 12 + x 12 a 22 = z 12 x 11 a 13 + x 12 a 23 = z 13 ⋯ x_{11}a_{11}+x_{12}a_{21}=z_{11}\\ x_{11}a_{12}+x_{12}a_{22}=z_{12}\\ x_{11}a_{13}+x_{12}a_{23}=z_{13}\\ \cdots x11a11+x12a21=z11x11a12+x12a22=z12x11a13+x12a23=z13⋯
所以:
∂ J ∂ x 11 = ∂ J ∂ z 11 ⋅ ∂ z 11 ∂ x 11 + ∂ J ∂ z 12 ⋅ ∂ z 12 ∂ x 11 + ∂ J ∂ z 13 ⋅ ∂ z 11 ∂ x 13 = δ 11 a 11 + δ 12 a 12 + δ 13 a 13 {\partial J\over\partial x_{11}} ={\partial J\over\partial z_{11}}\cdot{\partial z_{11}\over\partial x_{11}} +{\partial J\over\partial z_{12}}\cdot{\partial z_{12}\over\partial x_{11}} +{\partial J\over\partial z_{13}}\cdot{\partial z_{11}\over\partial x_{13}} =\delta_{11}a_{11}+\delta_{12}a_{12}+\delta_{13}a_{13}\\ ∂x11∂J=∂z11∂J⋅∂x11∂z11+∂z12∂J⋅∂x11∂z12+∂z13∂J⋅∂x13∂z11=δ11a11+δ12a12+δ13a13
于是:
∂ J ∂ X = [ δ 11 a 11 + δ 12 a 12 + δ 13 a 13 δ 11 a 21 + δ 12 a 22 + δ 13 a 23 δ 21 a 11 + δ 22 a 12 + δ 23 a 13 δ 21 a 21 + δ 22 a 22 + δ 23 a 23 δ 31 a 11 + δ 32 a 12 + δ 33 a 13 δ 21 a 21 + δ 22 a 22 + δ 23 a 23 ] = Δ ⋅ a T {\partial J\over\partial X}=\begin{bmatrix} \delta_{11}a_{11}+\delta_{12}a_{12}+\delta_{13}a_{13} & \delta_{11}a_{21}+\delta_{12}a_{22}+\delta_{13}a_{23}\\ \delta_{21}a_{11}+\delta_{22}a_{12}+\delta_{23}a_{13} & \delta_{21}a_{21}+\delta_{22}a_{22}+\delta_{23}a_{23}\\ \delta_{31}a_{11}+\delta_{32}a_{12}+\delta_{33}a_{13} & \delta_{21}a_{21}+\delta_{22}a_{22}+\delta_{23}a_{23}\\ \end{bmatrix}=\Delta\cdot a^T\\ ∂X∂J=⎣⎡δ11a11+δ12a12+δ13a13δ21a11+δ22a12+δ23a13δ31a11+δ32a12+δ33a13δ11a21+δ12a22+δ13a23δ21a21+δ22a22+δ23a23δ21a21+δ22a22+δ23a23⎦⎤=Δ⋅aT
也就是说:
∂ Z ∂ X = A T {\partial Z\over\partial X}=A^T\\ ∂X∂Z=AT
通过同样的推导方式可得到如下结论:
如果:
Z = K 1 Y , Y = X K 2 Z=K_1 Y , Y= XK_2 Z=K1Y,Y=XK2
那么 (要注意左乘和右乘的区别):
∂ Z ∂ X = K 1 T ⋅ n u m p y . o n e s l i k e ( Z ) ⋅ K 2 T {\partial Z\over \partial X}=K_1^T\cdot numpy.oneslike(Z)\cdot K_2^T ∂X∂Z=K1T⋅numpy.oneslike(Z)⋅K2T
这里为什么要乘以numpy.oneslike(Z)(numpy函数,shape和Z相同,但全为1),可以理解成上述 Δ \Delta Δ 作用,目的是为了保证形状
上面是比较直观的矩阵展开推导过程,现在用矩阵乘法公式进行求导过程。条件和上面一致,所以 X ⋅ A = Z X\cdot A=Z X⋅A=Z ,令 x i j , a j k , z i k x_{ij},a_{jk},z_{ik} xij,ajk,zik 分别为对应的元素,则:
z i k = ∑ j x i j a j k z_{ik}=\sum_j x_{ij}a_{jk}\\ zik=j∑xijajk
因此:
∂ J ∂ x i j = ∑ i j k ∂ J z i k ⋅ ∂ z i k ∂ x i j = ∑ k δ i k ⋅ ∂ z i k ∂ x i j = ∑ k δ i k ⋅ ∑ j a j k = ∑ k δ i k ⋅ a j k {\partial J\over\partial x_{ij}}=\sum_{ijk}{\partial J\over z_{ik}}\cdot {\partial z_{ik}\over \partial x_{ij}}=\sum_k \delta_{ik}\cdot {\partial z_{ik}\over \partial x_{ij}}=\sum_k \delta_{ik}\cdot \sum_ja_{jk}=\sum_k\delta_{ik}\cdot a_{jk}\\ ∂xij∂J=ijk∑zik∂J⋅∂xij∂zik=k∑δik⋅∂xij∂zik=k∑δik⋅j∑ajk=k∑δik⋅ajk
所以:
∂ J ∂ X = Δ ⋅ A T {\partial J\over\partial X}=\Delta\cdot A^T\\ ∂X∂J=Δ⋅AT
同理:
∂ J ∂ a j k = ∑ i δ i k ⋅ x i j {\partial J\over\partial a_{jk}}=\sum_i \delta_{ik}\cdot x_{ij}\\ ∂ajk∂J=i∑δik⋅xij
所以:
∂ J ∂ A = X T ⋅ Δ {\partial J\over \partial A}=X^T\cdot \Delta\\ ∂A∂J=XT⋅Δ
从上面展开式发现:
d Z d x i j = ∑ j a j k d Z d a j k = ∑ i x i j {dZ\over dx_{ij}}=\sum_j a_{jk}\\ {dZ\over da_{jk}}=\sum_i x_{ij}\\ dxijdZ=j∑ajkdajkdZ=i∑xij
所以:
d Z d X = n u m p y . o n e s l i k e ( Z ) ⋅ A T d Z d A = X T ⋅ n u m p y . o n e s l i k e ( Z ) {dZ\over dX}=numpy.oneslike(Z)\cdot A^T\\ \ \\ {dZ\over dA}=X^T\cdot numpy.oneslike(Z)\\ dXdZ=numpy.oneslike(Z)⋅AT dAdZ=XT⋅numpy.oneslike(Z)
这也就是矩阵链式求导使用numpy.oneslike的原因
2.1.2 numpy中的默认乘法,对应位置相乘 ( ⋅ ∗ \cdot * ⋅∗) 求导
假设有一个运算:
[ z 11 z 12 z 21 z 22 ] ⋅ ∗ [ σ 11 σ 12 σ 21 σ 22 ] = [ a 11 a 12 a 21 a 22 ] \begin{bmatrix} z_{11}&z_{12}\\ z_{21}&z_{22}\\ \end{bmatrix}\cdot *\begin{bmatrix} \sigma_{11}&\sigma_{12}\\ \sigma_{21}&\sigma_{22}\\ \end{bmatrix}=\begin{bmatrix} a_{11}&a_{12}\\ a_{21}&a_{22}\\ \end{bmatrix}\\ [z11z21z12z22]⋅∗[σ11σ21σ12σ22]=[a11a21a12a22]
且上述运算只是链式计算中的一环,即有 J = f ( A ) J=f(A) J=f(A) ,如果对 a 矩阵的每个元素求偏导,那么组合起来的矩阵一定是和z矩阵一样shape,即有:
∂ J ∂ A = [ δ 11 δ 12 δ 21 δ 22 ] {\partial J\over\partial A} =\begin{bmatrix} \delta_{11}&\delta_{12}\\ \delta_{21}&\delta_{22}\\ \end{bmatrix}\\ ∂A∂J=[δ11δ21δ12δ22]
在此基础上求解: ∂ J ∂ Z {\partial J\over \partial Z} ∂Z∂J
由于:
z 11 σ 11 = a 11 z 12 σ 12 = a 12 ⋯ z_{11}\sigma_{11}=a_{11}\\ z_{12}\sigma_{12}=a_{12}\\ \cdots\\ z11σ11=a11z12σ12=a12⋯
所以:
∂ J ∂ z 11 = ∂ J ∂ a 11 ⋅ ∂ a 11 ∂ z 11 = δ 11 ⋅ σ 11 {\partial J\over \partial z_{11}} ={\partial J\over\partial a_{11}}\cdot{\partial a_{11}\over\partial z_{11}} =\delta_{11}\cdot\sigma_{11}\\ ∂z11∂J=∂a11∂J⋅∂z11∂a11=δ11⋅σ11
于是:
∂ J ∂ Z = [ δ 11 ⋅ σ 11 δ 12 ⋅ σ 12 δ 21 ⋅ σ 21 δ 22 ⋅ σ 22 ] = δ ⋅ ∗ σ {\partial J\over\partial Z} =\begin{bmatrix} \delta_{11}\cdot\sigma_{11}&\delta_{12}\cdot\sigma_{12}\\ \delta_{21}\cdot\sigma_{21}&\delta_{22}\cdot\sigma_{22}\\ \end{bmatrix}=\delta\cdot * \sigma\\ ∂Z∂J=[δ11⋅σ11δ21⋅σ21δ12⋅σ12δ22⋅σ22]=δ⋅∗σ
其中 表示 对应的矩阵,通过同样的推导方式可以得到:
如果:
Z = K 1 Y , Y = X ⋅ ∗ K 2 Z=K_1Y,Y=X\cdot *K_2 Z=K1Y,Y=X⋅∗K2
那么:
∂ Z ∂ X = K 1 T ⋅ n u m p y . o n e s l i k e ( Z ) ⋅ ∗ K 2 {\partial Z\over \partial X}=K_1^T\cdot numpy.oneslike(Z)\cdot *K_2 ∂X∂Z=K1T⋅numpy.oneslike(Z)⋅∗K2
2.2 反向传播算法
反向传播算法本质是梯度更新,只不过它为了更方便计算机计算,先求出每一层的误差并缓存,然后再梯度更新
2.2.1 求每一层的误差 δ \delta δ
假设如下神经网络结构,包含2个hidden layer,3个输入feature,4个输出result,激活函数都是sigmoid,loss function使用cross entropy
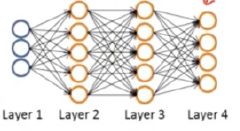
分解后如下图所示:
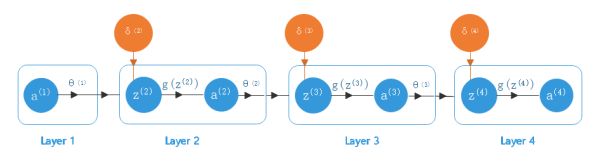
其中各个参数意义如下:
- a ( i ) a^{(i)} a(i):表示第 i 层激活值,其中 a ( 1 ) a^{(1)} a(1)为网络输入数据, a ( 4 ) a^{(4)} a(4) 为网络输出值
- z ( i ) z^{(i)} z(i) :表示第 i-1 层(上一层)网络输出值
- θ ( i ) \theta^{(i)} θ(i) :表示第 i 层网络参数
- δ ( i ) \delta^{(i)} δ(i) :表示第 i 层网络的误差,我们定义误差为 δ ( i ) = ∂ J ∂ z ( i ) \delta^{(i)}={\partial J\over\partial z^{(i)}} δ(i)=∂z(i)∂J
- g ( z ( i ) ) g(z^{(i)}) g(z(i)) :表示第 i 层的激活函数
由于采用cross entropy为损失函数,所以损失函数 J 有:
J = − [ y log a ( 4 ) + ( 1 − y ) log ( 1 − a ( 4 ) ) ] = − [ y log g ( z ( 4 ) ) + ( 1 − y ) log ( 1 − g ( z ( 4 ) ) ) ] J = -[y\log a^{(4)}+(1-y)\log (1-a^{(4)})]=-[y\log g(z^{(4)})+(1-y)\log (1-g(z^{(4)}))] J=−[yloga(4)+(1−y)log(1−a(4))]=−[ylogg(z(4))+(1−y)log(1−g(z(4)))]
又因为使用激活函数都是 σ = 1 e − x + 1 \sigma={1\over e^{-x}+1} σ=e−x+11 ,所以 g ′ ( z ( i ) ) = a ( i ) ⋅ ∗ ( 1 − a ( i ) ) g'(z^{(i)})=a^{(i)}\cdot *(1-a^{(i)}) g′(z(i))=a(i)⋅∗(1−a(i))
上述神经网络涉及两种运算:
- 点积( ⋅ \cdot ⋅ ): a ( i − 1 ) → z ( i ) a^{(i-1)}\rightarrow z^{(i)} a(i−1)→z(i)
- 点乘 ( ⋅ ∗ \cdot * ⋅∗) : z ( i ) → a ( i ) z^{(i)}\rightarrow a^{(i)} z(i)→a(i)
因此:
δ ( 4 ) = ∂ J ∂ z ( 4 ) = ∂ J ∂ a ( 4 ) ⋅ ∗ ∂ a ( 4 ) ∂ z ( 4 ) = a ( 4 ) − y a ( 4 ) ⋅ ∗ ( 1 − a ( 4 ) ) ⋅ ∗ g ′ ( z ( 4 ) ) = a ( 4 ) − y \delta^{(4)} ={\partial J\over\partial z^{(4)}} ={\partial J\over\partial a^{(4)}}\cdot *{\partial a^{(4)}\over\partial z^{(4)}} ={a^{(4)}-y\over a^{(4)}\cdot*(1-a^{(4)})}\cdot *g'(z^{(4)})=a^{(4)}-y\\ δ(4)=∂z(4)∂J=∂a(4)∂J⋅∗∂z(4)∂a(4)=a(4)⋅∗(1−a(4))a(4)−y⋅∗g′(z(4))=a(4)−y
根据链式求导:
δ ( 3 ) = ∂ J ∂ z ( 3 ) = ∂ J ∂ z ( 4 ) ⋅ ∂ z ( 4 ) ∂ a ( 3 ) ⋅ ∗ ∂ a ( 3 ) ∂ z ( 3 ) = δ ( 4 ) ⋅ ∂ z ( 4 ) ∂ a ( 3 ) ⋅ ∗ g ′ ( z ( 3 ) ) \delta^{(3)} ={\partial J\over\partial z^{(3)}} ={\partial J\over\partial z^{(4)}}\cdot{\partial z^{(4)}\over\partial a^{(3)}}\cdot *{\partial a^{(3)}\over\partial z^{(3)}} =\delta^{(4)}\cdot {\partial z^{(4)}\over\partial a^{(3)}}\cdot *g'(z^{(3)})\\ δ(3)=∂z(3)∂J=∂z(4)∂J⋅∂a(3)∂z(4)⋅∗∂z(3)∂a(3)=δ(4)⋅∂a(3)∂z(4)⋅∗g′(z(3))
根据2.1的矩阵求导法则,因为 z ( 4 ) = θ ( 3 ) ⋅ a ( 3 ) z^{(4)}=\theta^{(3)}\cdot a^{(3)} z(4)=θ(3)⋅a(3) ,所以:
δ ( 3 ) = ∂ J ∂ z ( 3 ) = ( θ ( 3 ) ) T ⋅ δ ( 4 ) ⋅ ∗ g ′ ( z ( 3 ) ) \delta^{(3)} ={\partial J\over\partial z^{(3)}} =(\theta^{(3)})^T\cdot \delta^{(4)}\cdot *g'(z^{(3)})\\ δ(3)=∂z(3)∂J=(θ(3))T⋅δ(4)⋅∗g′(z(3))
同理:
δ ( 2 ) = ( θ ( 2 ) ) T ⋅ δ ( 3 ) ⋅ ∗ g ′ ( z ( 2 ) ) \delta^{(2)}=(\theta^{(2)})^T\cdot\delta^{(3)}\cdot *g'(z^{(2)})\\ δ(2)=(θ(2))T⋅δ(3)⋅∗g′(z(2))
所以:
δ ( i ) = ∂ J ∂ z ( i ) = ( θ ( i ) ) T ⋅ δ ( i + 1 ) ⋅ ∗ g ′ ( z ( i ) ) \delta^{(i)} ={\partial J\over\partial z^{(i)}} =(\theta^{(i)})^T\cdot \delta^{(i+1)}\cdot *g'(z^{(i)})\\ δ(i)=∂z(i)∂J=(θ(i))T⋅δ(i+1)⋅∗g′(z(i))
2.2.2 求每一层权重的偏导数 ∂ J ∂ θ ( i ) \partial J\over\partial \theta^{(i)} ∂θ(i)∂J
求解了每一层的误差,接下来需要求我们需要更新的权重的梯度:
∂ J ∂ θ ( 3 ) = ∂ J ∂ z ( 4 ) ⋅ ∂ z ( 4 ) ∂ θ ( 3 ) = δ ( 4 ) ⋅ ∂ z ( 4 ) ∂ θ ( 3 ) {\partial J\over\partial\theta^{(3)}} ={\partial J\over\partial z^{(4)}}\cdot{\partial z^{(4)}\over\partial \theta^{(3)}} =\delta^{(4)}\cdot {\partial z^{(4)}\over\partial\theta^{(3)}}\\ ∂θ(3)∂J=∂z(4)∂J⋅∂θ(3)∂z(4)=δ(4)⋅∂θ(3)∂z(4)
根据2.1矩阵求导公式,因为 θ ( 3 ) ⋅ a ( 3 ) = z ( 4 ) \theta^{(3)}\cdot a^{(3)}=z^{(4)} θ(3)⋅a(3)=z(4) ,所以:
∂ J ∂ θ ( 3 ) = δ ( 4 ) ⋅ ( a ( 3 ) ) T {\partial J\over\partial\theta^{(3)}} =\delta^{(4)}\cdot (a^{(3)})^T\\ ∂θ(3)∂J=δ(4)⋅(a(3))T
同理:
∂ J ∂ θ ( 2 ) = δ ( 3 ) ⋅ ( a ( 2 ) ) T ∂ J ∂ θ ( 1 ) = δ ( 2 ) ⋅ ( a ( 1 ) ) T {\partial J\over\partial \theta^{(2)}} =\delta^{(3)}\cdot (a^{(2)})^T\\ \ \\ {\partial J\over\partial \theta^{(1)}} =\delta^{(2)}\cdot (a^{(1)})^T\\ ∂θ(2)∂J=δ(3)⋅(a(2))T ∂θ(1)∂J=δ(2)⋅(a(1))T
所以:
∂ J ∂ θ ( i ) = δ ( i + 1 ) ⋅ ( a ( i ) ) T {\partial J\over\partial \theta^{(i)}} =\delta^{(i+1)}\cdot (a^{(i)})^T\\ ∂θ(i)∂J=δ(i+1)⋅(a(i))T
从而就可以应用梯度更新公式了
2.2.3 反向传播算法总结
第 i 层的误差,与对应层使用的激活函数相关:
δ ( i ) = ∂ J ∂ z ( i ) = ( θ ( i ) ) T ⋅ δ ( i + 1 ) ⋅ ∗ g ′ ( z ( i ) ) \delta^{(i)} ={\partial J\over\partial z^{(i)}} =(\theta^{(i)})^T\cdot \delta^{(i+1)}\cdot *g'(z^{(i)})\\ δ(i)=∂z(i)∂J=(θ(i))T⋅δ(i+1)⋅∗g′(z(i))
最后一层误差,需要结合损失函数求导得到
第 i 层的梯度:
∂ J ∂ θ ( i ) = δ ( i + 1 ) ⋅ ( a ( i ) ) T {\partial J\over\partial \theta^{(i)}} =\delta^{(i+1)}\cdot (a^{(i)})^T\\ ∂θ(i)∂J=δ(i+1)⋅(a(i))T
3 梯度爆炸和梯度消失
3.1 梯度爆炸消失对反向传播的影响
梯度消失和梯度爆炸问题,字面上理解就是 θ ( i ) = θ ( i ) − α ∂ J ∂ θ ( i ) \theta^{(i)} = \theta^{(i)} -\alpha{\partial J\over \partial\theta^{(i)}} θ(i)=θ(i)−α∂θ(i)∂J 中的 ∂ J ∂ θ ( i ) {\partial J\over\partial \theta^{(i)}} ∂θ(i)∂J 梯度项,接近0或者接近无穷。下面特例说明梯度消失梯度爆炸在反向传播中的表现。
因为:
∂ J ∂ θ ( i ) = δ ( i + 1 ) ⋅ ( a ( i ) ) T {\partial J\over\partial \theta^{(i)}} =\delta^{(i+1)}\cdot (a^{(i)})^T ∂θ(i)∂J=δ(i+1)⋅(a(i))T
假设网络采用线性激活,即不采用激活函数,即:
δ ( i + 1 ) = ∂ J ∂ z ( i + 1 ) = ( θ ( i + 1 ) ) T ⋅ δ ( i + 2 ) ⋅ ∗ g ′ ( z ( i + 1 ) ) = ( θ ( i + 1 ) ) T ⋅ δ ( i + 2 ) \delta^{(i+1)} ={\partial J\over\partial z^{(i+1)}} =(\theta^{(i+1)})^T\cdot \delta^{(i+2)}\cdot *g'(z^{(i+1)})=(\theta^{(i+1)})^T\cdot \delta^{(i+2)}\\ δ(i+1)=∂z(i+1)∂J=(θ(i+1))T⋅δ(i+2)⋅∗g′(z(i+1))=(θ(i+1))T⋅δ(i+2)
令每一层为权重 θ ( i ) = [ k k ] \theta^{(i)}=\begin{bmatrix} k&\\ &k \end{bmatrix} θ(i)=[kk] ,那么:
δ ( i ) = ∏ l = i L − 1 θ ( i ) ⋅ δ ( L ) = [ k L − 1 − i k L − 1 − i ] ⋅ δ ( L ) \delta^{(i)} =\prod_{l=i}^{L-1}\theta^{(i)}\cdot \delta^{(L)} =\begin{bmatrix} k^{L-1-i}&\\ &k^{L-1-i}\\ \end{bmatrix}\cdot \delta^{(L)}\\ δ(i)=l=i∏L−1θ(i)⋅δ(L)=[kL−1−ikL−1−i]⋅δ(L)
其中 L 表示网络层数,当网络很深时, L − 1 − i → ∞ L-1-i\rightarrow\infty L−1−i→∞ ,且 a ( i ) a^{(i)} a(i) 在计算梯度时,做常数处理,所以梯度的值和上一层的误差成正相关所以:
k < 1 ⇒ δ → 0 ⇒ ∂ J ∂ θ → 0 k > 1 ⇒ δ → ∞ ⇒ ∂ J ∂ θ → ∞ k<1\Rightarrow \delta\rightarrow 0\Rightarrow{\partial J\over \partial\theta}\rightarrow 0\\ \ \\ k> 1\Rightarrow \delta\rightarrow \infty\Rightarrow{\partial J\over \partial\theta}\rightarrow \infty\\ k<1⇒δ→0⇒∂θ∂J→0 k>1⇒δ→∞⇒∂θ∂J→∞
小结:当网络很深时,深层网络的梯度更新与输出层误差无关,即梯度不一定朝着梯度变小的方向更新。
3.2 梯度爆炸消失对前馈网络的影响
条件还是和上述一致,那么:
y ^ = σ ( ∏ l = 1 L θ ( l ) ⋅ X ) = σ ( [ k L k L ] ⋅ X ) \hat{y} =\sigma(\prod_{l=1}^L \theta^{(l)}\cdot X) =\sigma(\begin{bmatrix} k^L&\\ &k^L\\ \end{bmatrix}\cdot X)\\ y^=σ(l=1∏Lθ(l)⋅X)=σ([kLkL]⋅X)
当网络很深, L → ∞ L\rightarrow \infty L→∞ ,所以:
k < 1 ⇒ k L → 0 ⇒ y ^ → 0 k > 1 ⇒ k L → ∞ ⇒ y ^ → 1 k<1\Rightarrow k^L\rightarrow 0 \Rightarrow\hat{y}\rightarrow 0\\ k>1\Rightarrow k^L\rightarrow \infty\Rightarrow \hat{y}\rightarrow 1\\ k<1⇒kL→0⇒y^→0k>1⇒kL→∞⇒y^→1
小结:当存在梯度爆炸或梯度消失时,网络的输出和网络的输入X不相关。
3.3 梯度爆炸、梯度消失原因总结
通过3.1、3.2的总结,我们发现如果权重矩阵设置不当,即:
- 所有权重 Θ > I \Theta>I Θ>I ,容易产生梯度爆炸问题
- 所有权重 Θ < I \Theta<I Θ<I ,容易产生梯度消失问题
所以权重初始化很重要,至于怎么初始化,我们后续再讲解