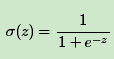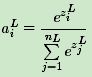在监督学习中,传统的机器学习算法优化过程是采用一个合适的损失函数度量训练样本输出损失,对损失函数进行优化求最小化的极值,相应一系列线性系数矩阵W,偏置向量b即为我们的最终结果。在DNN中,损失函数优化极值求解的过程一般采用梯度下降法、牛顿法或拟牛顿法等迭代方法来迭代完成。对DNN的损失函数用梯度下降法进行迭代优化求极小值的过程即为反向传播算法,可以使用多种损失函数和激活函数。
1. 均方差损失函数+Sigmoid激活函数
Sigmoid激活函数的表达式为:
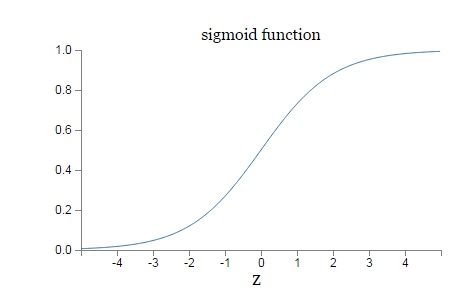
σ(z)的函数图像如下:
对于Sigmoid,当z的取值越来越大后,函数曲线变得越来越平缓,意味着此时的导数σ′(z)也越来越小。同样的,当z的取值越来越小时,也有这个问题。仅仅在z取值为0附近时,导数σ′(z)的取值较大。
缺点:反向传播算法中,每一层向前递推都要乘以σ′(z),得到梯度变化值。Sigmoid的这个曲线意味着在大多数时候,我们的梯度变化值很小,导致我们的W、b更新到极值的速度较慢,也就是我们的算法收敛速度较慢。
2. 交叉熵损失函数+Sigmoid激活函数
Sigmoid的函数特性导致反向传播算法收敛速度慢的问题,有两种改进策略:1)换激活函数;2)使用交叉熵损失函数来代替均方差损失函数:使用交叉熵得到的的δl梯度表达式没有σ′(z),梯度为预测值和真实值的差距,这样求得的Wl,bl也不包含σ′(z),因此避免了反向传播收敛速度慢的问题。
3. 对数似然损失函数和softmax激活函数
上述输出是连续可导的值,但如果是分类问题,输出是一个个的类别时,假设对三个类别进行分类,输出层应该有三个神经元,假设第一个神经元对应类别一,第二个对应类别二,第三个对应类别三,这样我们期望的输出应该是(1,0,0)、(0,1,0)和(0,0,1)这三种。即样本真实类别对应的神经元输出应该无限接近或者等于1,而非改样本真实输出对应的神经元的输出应该无限接近或者等于0。或者输出层的神经元对应的输出是若干个概率值,这若干个概率值即DNN模型对于输入值对于各类别的输出预测,同时满足概率模型,这若干个概率值之和应该等于1。分类模型要求是输出层神经元输出的值在0到1之间,同时所有输出值之和为1。
Softmax激活函数的表达式为:
其中,nL是输出层第L层的神经元个数,或者说我们的分类问题的类别数。
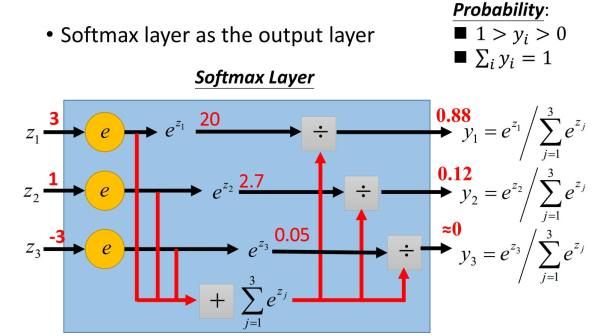
Softmax激活函数在前向传播算法时:
反向传播:假设真实类别是第i类,则其他不属于第i类序号对应的神经元的梯度导数直接为0。对于真实类别第i类,它的WiL对应的梯度为(aiL−1)aiL−1,biL的梯度为aiL−1。举个例子,假如我们对于第2类的训练样本,通过前向算法计算的未激活输出为(1,5,3),则我们得到softmax激活后的概率输出为:(0.015,0.866,0.117)。由于我们的类别是第二类,则反向传播的梯度应该为:(0.015,0.866-1,0.117)。
梯度消失&梯度爆炸:在反向传播算法过程中,由于使用矩阵求导的链式法则,有一大串连乘,如果连乘的数字在每层都是小于1的,则梯度越往前乘越小,导致梯度消失;连乘的数字在每层都是大于1的,则梯度越往前乘越大,导致梯度爆炸。
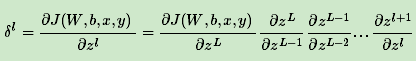
1)对于梯度爆炸,一般可以通过调整DNN模型中的初始化参数来解决;
2)对于梯度消失,可部分解决梯度消失问题的办法是使用ReLU(Rectified Linear Unit)激活函数,ReLU在卷积神经网络CNN中已得到广泛应用。
ReLU激活函数表达式为:
![]()
大于等于0则不变,小于0则激活后为0。