python面向对象、向量化来实现神经网络和反向传播(三)
现在,我们要根据前面的算法,实现一个基本的全连接神经网络,这并不需要太多代码。我们在这里依然采用面向对象设计。
理论知识参考:https://www.zybuluo.com/hanbingtao/note/476663,这里只撸代码。
由于自身的对象编程意识比较弱,这里重点分析下算法的面向对象编程。
1. 神经网络的实现(面向对象)
首先,本算法的实现有几个类组成:
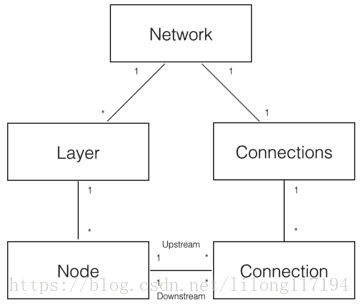
如上图,可以分解出5个领域对象来实现神经网络:
- Network 神经网络对象,提供API接口。它由若干层对象组成以及连接对象组成。
- Layer 层对象,由多个节点组成。
- Node 节点对象计算和记录节点自身的信息(比如输出值、误差项等),以及与这个节点相关的上下游的连接。
- Connection 每个连接对象都要记录该连接的权重。
- Connections 仅仅作为Connection的集合对象,提供一些集合操作。
代码具体如下:
# -*- coding: utf-8 -*-
#!/usr/bin/env python
# -*- coding: UTF-8 -*-
import random
from numpy import *
# 定义激活函数
def sigmoid(inX):
return 1.0 / (1 + exp(-inX))
# 定义节点类:负责记录和维护节点自身信息以及与这个节点相关的上下游连接,实现输出值和误差项的计算。
class Node(object):
def __init__(self, layer_index, node_index):
'''
构造节点对象。
layer_index: 节点所属的层的编号
node_index: 节点的编号
'''
self.layer_index = layer_index
self.node_index = node_index
self.downstream = []
self.upstream = []
self.output = 0
self.delta = 0
def set_output(self, output):
'''
设置节点的输出值。如果节点属于输入层会用到这个函数。
'''
self.output = output
def calc_output(self):
'''
根据式1计算节点的输出
'''
output = reduce(lambda ret, conn: ret + conn.upstream_node.output * conn.weight,
self.upstream, 0)
self.output = sigmoid(output)
def append_downstream_connection(self, conn):
'''
添加一个到下游节点的连接
'''
self.downstream.append(conn)
def append_upstream_connection(self, conn):
'''
添加一个到上游节点的连接
'''
self.upstream.append(conn)
def calc_hidden_layer_delta(self):
'''
节点属于隐藏层时,根据式4计算delta
'''
downstream_delta = reduce(lambda ret, conn: ret + conn.downstream_node.delta * conn.weight,
self.downstream, 0.0)
self.delta = self.output * (1 - self.output) * downstream_delta
def calc_output_layer_delta(self, label):
'''
节点属于输出层时,根据式3计算delta
'''
self.delta = self.output * (1 - self.output) * (label - self.output)
def __str__(self):
'''
打印节点的信息
'''
node_str = '%u-%u: output: %f delta: %f' % (self.layer_index, self.node_index, self.output, self.delta)
downstream_str = reduce(lambda ret, conn: ret + '\n\t' + str(conn), self.downstream, '')
upstream_str = reduce(lambda ret, conn: ret + '\n\t' + str(conn), self.upstream, '')
return node_str + '\n\tdownstream:' + downstream_str + '\n\tupstream:' + upstream_str
# ConstNode对象,为了实现一个输出恒为1的节点(计算偏置项时需要)
class ConstNode(object):
def __init__(self, layer_index, node_index):
'''
构造节点对象
layer_index: 节点所属的层的编号
node_index: 节点的编号
'''
self.layer_index = layer_index
self.node_index = node_index
self.downstream = []
self.output = 1
def append_downstream_connection(self, conn):
'''
添加一个到下游节点的连接
'''
self.downstream.append(conn)
def calc_hidden_layer_delta(self):
'''
节点属于隐藏层时,根据式4计算delta
'''
downstream_delta = reduce(lambda ret, conn: ret + conn.downstream_node.delta * conn.weight,
self.downstream, 0.0)
self.delta = self.output * (1 - self.output) * downstream_delta
def __str__(self):
'''
打印节点的信息
'''
node_str = '%u-%u: output: 1' % (self.layer_index, self.node_index)
downstream_str = reduce(lambda ret, conn: ret + '\n\t' + str(conn), self.downstream, '')
return node_str + '\n\tdownstream:' + downstream_str
# Layer对象,负责初始化一层。此外,作为Node的集合对象,提供对Node集合的操作
class Layer(object):
def __init__(self, layer_index, node_count):
'''
初始化一层
layer_index: 层编号
node_count: 层所包含的节点个数
'''
self.layer_index = layer_index
self.nodes = [] # 节点对象存储到数列中
for i in range(node_count): # 对每层的各个节点建立节点对象
self.nodes.append(Node(layer_index, i))
self.nodes.append(ConstNode(layer_index, node_count)) # 节点数列添加ConstNode对象,为了实现一个输出恒为1的节点
def set_output(self, data):
'''
设置层的输出。当层是输入层时会用到。
'''
for i in range(len(data)): # 直接让每个节点的输出就是输入的向量
self.nodes[i].set_output(data[i])
def calc_output(self):
'''
计算层的输出向量
'''
for node in self.nodes[:-1]:
node.calc_output()
def dump(self):
'''
打印层的信息
'''
for node in self.nodes:
print node
# Connection对象,主要职责是记录连接的权重,以及这个连接所关联的上下游节点
class Connection(object):
def __init__(self, upstream_node, downstream_node):
'''
初始化连接,权重初始化为是一个很小的随机数
upstream_node: 连接的上游节点
downstream_node: 连接的下游节点
'''
self.upstream_node = upstream_node
self.downstream_node = downstream_node
self.weight = random.uniform(-0.1, 0.1)
self.gradient = 0.0
def calc_gradient(self):
'''
计算梯度
'''
self.gradient = self.downstream_node.delta * self.upstream_node.output
def update_weight(self, rate):
'''
根据梯度下降算法更新权重
'''
self.calc_gradient()
self.weight += rate * self.gradient
def get_gradient(self):
'''
获取当前的梯度
'''
return self.gradient
def __str__(self):
'''
打印连接信息
'''
return '(%u-%u) -> (%u-%u) = %f' % (
self.upstream_node.layer_index,
self.upstream_node.node_index,
self.downstream_node.layer_index,
self.downstream_node.node_index,
self.weight)
# Connections对象,提供Connection集合操作
class Connections(object):
def __init__(self):
self.connections = []
def add_connection(self, connection):
self.connections.append(connection)
def dump(self):
for conn in self.connections:
print conn
# Network对象,提供API
class Network(object):
def __init__(self, layers):
'''
初始化一个全连接神经网络
layers: 二维数组,描述神经网络每层节点数
'''
self.connections = Connections()
self.layers = [] # 存储每层网络的信息:第几层网络,每层网络的节点数,每个节点的信息
# 进行其他对象的调用和初始化连接权重
layer_count = len(layers)
node_count = 0
for i in range(layer_count): # 定义Layer对象,layers数组层存放的是每个层的节点对象
self.layers.append(Layer(i, layers[i]))
#print 'layers:\n',self.layers[i].dump()
for layer in range(layer_count - 1): # 遍历第一层和第二层到第三层,进行节点间的连接
#print 'layer:',layer
connections = [Connection(upstream_node, downstream_node)
for upstream_node in self.layers[layer].nodes
for downstream_node in self.layers[layer + 1].nodes[:-1]
]
print len(connections ) # 打印权重个数
for conn in connections:
#print 'conn:::',conn
self.connections.add_connection(conn) # 对于两层间的连接,进行集合操作
conn.downstream_node.append_upstream_connection(conn) # 初始化全连接网络的权重
conn.upstream_node.append_downstream_connection(conn)
#print 'conn.upstream_node:',conn.upstream_node
#print 'conn.downstream_node:',conn.downstream_node
def train(self, labels, data_set, rate, epoch):
'''
训练神经网络
labels: 数组,训练样本标签。每个元素是一个样本的标签。
data_set: 二维数组,训练样本特征。每个元素是一个样本的特征。
'''
for i in range(epoch): # 遍历每一次迭代
for d in range(len(data_set)): # 遍历每一个样本,进行每一个样本的训练
self.train_one_sample(labels[d], data_set[d], rate)
# print 'sample %d training finished' % d
def train_one_sample(self, label, sample, rate):
'''
内部函数,用一个样本训练网络
'''
self.predict(sample)
self.calc_delta(label)
self.update_weight(rate)
def calc_delta(self, label):
'''
内部函数,计算每个节点的delta
'''
output_nodes = self.layers[-1].nodes
for i in range(len(label)): # 计算输出层的每个节点的误差项
output_nodes[i].calc_output_layer_delta(label[i])
for layer in self.layers[-2::-1]: # 依次计算隐层和输入层节点的误差项
for node in layer.nodes:
node.calc_hidden_layer_delta()
def update_weight(self, rate):
'''
内部函数,更新每个连接权重
'''
for layer in self.layers[:-1]:
for node in layer.nodes:
for conn in node.downstream:
conn.update_weight(rate)
def calc_gradient(self):
'''
内部函数,计算每个连接的梯度
'''
for layer in self.layers[:-1]:
for node in layer.nodes:
for conn in node.downstream:
conn.calc_gradient()
def get_gradient(self, label, sample):
'''
获得网络在一个样本下,每个连接上的梯度
label: 样本标签
sample: 样本输入
'''
self.predict(sample)
self.calc_delta(label)
self.calc_gradient()
def predict(self, sample):
'''
根据输入的样本预测输出值(前向传播)
sample: 数组,样本的特征,也就是网络的输入向量
'''
self.layers[0].set_output(sample) # 第一层的输出
for i in range(1, len(self.layers)): # 后面两层的输出计算
self.layers[i].calc_output()
return map(lambda node: node.output, self.layers[-1].nodes[:-1]) # 返回输出层的每个节点的输出
def dump(self):
for layer in self.layers:
layer.dump()
class Normalizer(object):
def __init__(self):
self.mask = [0x1, 0x2, 0x4, 0x8, 0x10, 0x20, 0x40, 0x80 ] # 1,2,4,8,16,32,64,128
def norm(self, number):
return map(lambda m: 0.9 if number & m else 0.1, self.mask) # & 是位运算,and 是逻辑运算。
def denorm(self, vec):
binary = map(lambda i: 1 if i > 0.5 else 0, vec)
for i in range(len(self.mask)):
binary[i] = binary[i] * self.mask[i]
return reduce(lambda x,y: x + y, binary)
def mean_square_error(vec1, vec2):
return 0.5 * reduce(lambda a, b: a + b,
map(lambda v: (v[0] - v[1]) * (v[0] - v[1]),
zip(vec1, vec2)
)
)
# 构造训练数据集
def train_data_set():
normalizer = Normalizer()
data_set = []
labels = []
for i in range(0, 256, 8):
n = normalizer.norm(int(random.uniform(0, 256)))
#print 'n:',n
data_set.append(n)
labels.append(n)
return labels, data_set
# 训练网络
def train(network):
labels, data_set = train_data_set()
#print 'labels, data_set:',labels, '\n',data_set
network.train(labels, data_set, 0.2, 100)
def test(network, data):
normalizer = Normalizer()
norm_data = normalizer.norm(data)
predict_data = network.predict(norm_data)
print '\ttestdata(%u)\tpredict(%u)' % (
data, normalizer.denorm(predict_data))
def correct_ratio(network):
normalizer = Normalizer()
correct = 0.0;
for i in range(256):
if normalizer.denorm(network.predict(normalizer.norm(i))) == i:
correct += 1.0
print 'correct_ratio: %.2f%%' % (correct / 256 * 100)
if __name__ == '__main__':
net = Network([8, 3, 8])
train(net)
net.dump()
correct_ratio(net)
运行结果:
27
32
0-0: output: 0.100000 delta: 0.000946
downstream:
(0-0) -> (1-0) = 0.018301
(0-0) -> (1-1) = -2.615214
(0-0) -> (1-2) = 0.622107
upstream:
0-1: output: 0.100000 delta: 0.001988
downstream:
(0-1) -> (1-0) = 0.673368
(0-1) -> (1-1) = 0.341187
(0-1) -> (1-2) = 0.489427
upstream:
...
...
...
2-7: output: 0.437030 delta: 0.113907
downstream:
upstream:
(1-0) -> (2-7) = 1.519429
(1-1) -> (2-7) = -1.701739
(1-2) -> (2-7) = 0.632402
(1-3) -> (2-7) = 0.005931
2-8: output: 1
downstream:
correct_ratio: 6.64%这里有几个地方需要注意下:
- 训练数据和测试数据都是自己构建的,把数字转化为相对应的8维特征向量。
- 上述代码的
Network([8, 3, 8]),构建的是8x3x8的网络,所以正确率比较低,下面通过改变网络的层数和迭代次数,学习率后会发现正确率有所提升。 - 这段代码的难度主要是在构建类,我也是花了很长时间分析类的构建和类间的关系,可能还是面向对象的代码写的比较少,最好自己在纸上写下来,把类属性和方法都通过画图的方式联系起来,毕竟直接看代码的话会来回翻看,不方便。
- 神经网络的编写用面向对象感觉还是有点麻烦的,应该更多的用向量化编程,不仅提高了运行速度,而且更容易理解,本文就当是面向对象编程练手了。
- 本代码中涉及的公式推到参看:
https://www.zybuluo.com/hanbingtao/note/476663
下面改变网络层后的运行结果:
(1)Network([8, 5, 8])
if __name__ == '__main__':
net = Network([8, 5, 8])
train(net)
net.dump()
correct_ratio(net)正确率:
correct_ratio: 21.09%(2)Network([8, 8, 8])
if __name__ == '__main__':
net = Network([8, 8, 8])
train(net)
net.dump()
correct_ratio(net)正确率:
correct_ratio: 36.72%(3)Network([8, 20, 8])
if __name__ == '__main__':
net = Network([8, 20, 8])
train(net)
net.dump()
correct_ratio(net)正确率:
correct_ratio: 92.19%可以看出随着网络层的增加,正确率是逐渐增高的,但也不是绝对的增高,而且每次的运行结果可能不同,最好的一次是92.19%的正确率,这里主要是关注编程的方法和思想,而训练数据和测试数据的构建不是很科学,所以正确率不稳定。
2. 向量化编程
在经历了漫长的训练之后,我们可能会想到,肯定有更好的办法!是的,程序员们,现在我们需要告别面向对象编程了,转而去使用另外一种更适合深度学习算法的编程方式:向量化编程。主要有两个原因:一个是我们事实上并不需要真的去定义Node、Connection这样的对象,直接把数学计算实现了就可以了;另一个原因,是底层算法库会针对向量运算做优化(甚至有专用的硬件,比如GPU),程序效率会提升很多。所以,在深度学习的世界里,我们总会想法设法的把计算表达为向量的形式。
下面,我们用向量化编程的方法,重新实现前面的全连接神经网络。
首先,我们需要把所有的计算都表达为向量的形式。对于全连接神经网络来说,主要有三个计算公式。
前向计算,我们发现式2已经是向量化的表达了:

现在,我们根据上面几个公式,重新实现一个类:FullConnectedLayer。它实现了全连接层的前向和后向计算:
#!/usr/bin/env python
# -*- coding: UTF-8 -*-
import random
import numpy as np
#from activators import SigmoidActivator, IdentityActivator
# Sigmoid激活函数类
class SigmoidActivator(object):
def forward(self, weighted_input):
return 1.0 / (1.0 + np.exp(-weighted_input))
def backward(self, output):
return output * (1 - output)
# 全连接层实现类
class FullConnectedLayer(object):
def __init__(self, input_size, output_size, activator):
'''
构造函数
input_size: 本层输入向量的维度
output_size: 本层输出向量的维度
activator: 激活函数
'''
self.input_size = input_size
self.output_size = output_size
self.activator = activator
# 权重数组W
self.W = np.random.uniform(-0.1, 0.1,(output_size, input_size))
# 偏置项b
self.b = np.zeros((output_size, 1))
# 输出向量
self.output = np.zeros((output_size, 1))
def forward(self, input_array):
'''
前向计算
input_array: 输入向量,维度必须等于input_size
'''
# 式2
self.input = input_array
self.output = self.activator.forward(np.dot(self.W, input_array) + self.b)
def backward(self, delta_array):
'''
反向计算W和b的梯度
delta_array: 从上一层传递过来的误差项
'''
# 式8
self.delta = self.activator.backward(self.input) * np.dot(self.W.T, delta_array)
self.W_grad = np.dot(delta_array, self.input.T)
self.b_grad = delta_array
def update(self, learning_rate):
'''
使用梯度下降算法更新权重
'''
self.W += learning_rate * self.W_grad
self.b += learning_rate * self.b_grad
def dump(self):
print 'W: %s\nb:%s' % (self.W, self.b)
# 神经网络类
class Network(object):
def __init__(self, layers):
'''
构造函数
'''
self.layers = []
for i in range(len(layers) - 1):
self.layers.append(
FullConnectedLayer(layers[i], layers[i+1],SigmoidActivator())
)
def predict(self, sample):
'''
使用神经网络实现预测
sample: 输入样本
'''
output = sample
for layer in self.layers:
layer.forward(output)
output = layer.output
return output
def train(self, labels, data_set, rate, epoch):
'''
训练函数
labels: 样本标签
data_set: 输入样本
rate: 学习速率
epoch: 训练轮数
'''
for i in range(epoch):
for d in range(len(data_set)):
self.train_one_sample(labels[d], data_set[d], rate)
def train_one_sample(self, label, sample, rate):
self.predict(sample)
self.calc_gradient(label)
self.update_weight(rate)
def calc_gradient(self, label):
delta = self.layers[-1].activator.backward(self.layers[-1].output) * (label - self.layers[-1].output)
for layer in self.layers[::-1]:
layer.backward(delta)
delta = layer.delta
return delta
def update_weight(self, rate):
for layer in self.layers:
layer.update(rate)
def dump(self):
for layer in self.layers:
layer.dump()
def loss(self, output, label):
return 0.5 * ((label - output) * (label - output)).sum()
def transpose(args):
return map(
lambda arg: map(lambda line: np.array(line).reshape(len(line), 1), arg), args)
class Normalizer(object):
def __init__(self):
self.mask = [0x1, 0x2, 0x4, 0x8, 0x10, 0x20, 0x40, 0x80]
def norm(self, number):
data = map(lambda m: 0.9 if number & m else 0.1, self.mask)
return np.array(data).reshape(8, 1)
def denorm(self, vec):
binary = map(lambda i: 1 if i > 0.5 else 0, vec[:,0])
for i in range(len(self.mask)):
binary[i] = binary[i] * self.mask[i]
return reduce(lambda x,y: x + y, binary)
def train_data_set():
normalizer = Normalizer()
data_set = []
labels = []
for i in range(256):
n = normalizer.norm(i)
data_set.append(n)
labels.append(n)
return labels, data_set
def correct_ratio(network):
normalizer = Normalizer()
correct = 0.0;
for i in range(0, 256, 8):
if normalizer.denorm(network.predict(normalizer.norm(i))) == i:
correct += 1.0
print 'correct_ratio: %.2f%%' % (correct / 32 * 100)
def test():
labels, data_set = transpose(train_data_set())
net = Network([8, 20, 8])
rate = 0.5
mini_batch = 20
epoch = 10
for i in range(epoch):
net.train(labels, data_set, rate, mini_batch)
print 'after epoch %d loss: %f' % ( (i + 1),
net.loss(labels[-1], net.predict(data_set[-1]))
)
rate /= 2
correct_ratio(net)
if __name__ == '__main__':
test()
运行结果:
after epoch 1 loss: 0.001780
after epoch 2 loss: 0.000960
after epoch 3 loss: 0.000747
after epoch 4 loss: 0.000691
after epoch 5 loss: 0.000674
after epoch 6 loss: 0.000667
after epoch 7 loss: 0.000665
after epoch 8 loss: 0.000663
after epoch 9 loss: 0.000663
after epoch 10 loss: 0.000663
correct_ratio: 100.00%同样这里的训练数据和测试数据也不是很科学,所以正确率达到了100%,这里旨在学习编程的过程和思想。
上面这个类一举取代了原先的Layer、Node、Connection等类,不但代码更加容易理解,而且运行速度也快了很多倍。
向量化的编程看着清爽多了。。
3. 神经网络实战——手写数字识别
针对这个任务,我们采用业界非常流行的MNIST数据集。MNIST大约有60000个手写字母的训练样本,我们使用它训练我们的神经网络,然后再用训练好的网络去识别手写数字。
手写数字识别是个比较简单的任务,数字只可能是0-9中的一个,这是个10分类问题。
输入层节点数是确定的。因为MNIST数据集每个训练数据是28*28的图片,共784个像素,因此,输入层节点数应该是784,每个像素对应一个输入节点。
输出层节点数也是确定的。因为是10分类,我们可以用10个节点,每个节点对应一个分类。输出层10个节点中,输出最大值的那个节点对应的分类,就是模型的预测结果。
隐藏层节点数量是不好确定的,从1到100万都可以。下面有几个经验公式:

因此,我们可以先根据上面的公式设置一个隐藏层节点数。如果有时间,我们可以设置不同的节点数,分别训练,看看哪个效果最好就用哪个。我们先拍一个,设隐藏层节点数为300吧。
对于3层784*300*10的全连接网络,总共有300*(784+1)+10*(300+1)=238510个参数!神经网络之所以强大,是它提供了一种非常简单的方法去实现大量的参数。目前百亿参数、千亿样本的超大规模神经网络也是有的。因为MNIST只有6万个训练样本,参数太多了很容易过拟合,效果反而不好。
代码实现
首先,我们需要把MNIST数据集处理为神经网络能够接受的形式。MNIST训练集的文件格式可以参考官方网站,这里不在赘述。每个训练样本是一个28*28的图像,我们按照行优先,把它转化为一个784维的向量。每个标签是0-9的值,我们将其转换为一个10维的one-hot向量:如果标签值为n,我们就把向量的第n维(从0开始编号)设置为0.9,而其它维设置为0.1。例如,向量[0.1,0.1,0.9,0.1,0.1,0.1,0.1,0.1,0.1,0.1]表示值2。
- 首先是导入向量化的fc.py文件。
#!/usr/bin/env python
# -*- coding: UTF-8 -*-
import random
import numpy as np
#from activators import SigmoidActivator, IdentityActivator
# Sigmoid激活函数类
class SigmoidActivator(object):
def forward(self, weighted_input):
return 1.0 / (1.0 + np.exp(-weighted_input))
def backward(self, output):
return output * (1 - output)
# 全连接层实现类
class FullConnectedLayer(object):
def __init__(self, input_size, output_size, activator):
'''
构造函数
input_size: 本层输入向量的维度
output_size: 本层输出向量的维度
activator: 激活函数
'''
self.input_size = input_size
self.output_size = output_size
self.activator = activator
# 权重数组W
self.W = np.random.uniform(-0.1, 0.1,(output_size, input_size))
# 偏置项b
self.b = np.zeros((output_size, 1))
# 输出向量
self.output = np.zeros((output_size, 1))
def forward(self, input_array):
'''
前向计算
input_array: 输入向量,维度必须等于input_size
'''
# 式2
self.input = input_array
self.output = self.activator.forward(np.dot(self.W, input_array) + self.b)
def backward(self, delta_array):
'''
反向计算W和b的梯度
delta_array: 从上一层传递过来的误差项
'''
# 式8
self.delta = self.activator.backward(self.input) * np.dot(self.W.T, delta_array)
self.W_grad = np.dot(delta_array, self.input.T)
self.b_grad = delta_array
def update(self, learning_rate):
'''
使用梯度下降算法更新权重
'''
self.W += learning_rate * self.W_grad
self.b += learning_rate * self.b_grad
def dump(self):
print 'W: %s\nb:%s' % (self.W, self.b)
# 神经网络类
class Network(object):
def __init__(self, layers):
'''
构造函数
'''
self.layers = []
for i in range(len(layers) - 1):
self.layers.append(
FullConnectedLayer(layers[i], layers[i+1],SigmoidActivator())
)
def predict(self, sample):
'''
使用神经网络实现预测
sample: 输入样本
'''
output = sample
for layer in self.layers:
layer.forward(output)
output = layer.output
#print 'output:',output
return output
def train(self, labels, data_set, rate, epoch):
'''
训练函数
labels: 样本标签
data_set: 输入样本
rate: 学习速率
epoch: 训练轮数
'''
for i in range(epoch):
for d in range(len(data_set)):
self.train_one_sample(labels[d], data_set[d], rate)
def train_one_sample(self, label, sample, rate):
self.predict(sample)
self.calc_gradient(label)
self.update_weight(rate)
def calc_gradient(self, label):
delta = self.layers[-1].activator.backward(self.layers[-1].output) * (label - self.layers[-1].output)
for layer in self.layers[::-1]:
layer.backward(delta)
delta = layer.delta
return delta
def update_weight(self, rate):
for layer in self.layers:
layer.update(rate)
def dump(self):
for layer in self.layers:
layer.dump()
def loss(self, output, label):
return 0.5 * ((label - output) * (label - output)).sum()- 手写体实现的py文件
#!/usr/bin/env python
# -*- coding: UTF-8 -*-
import struct
import fc
from datetime import datetime
import numpy as np
# 数据加载器基类
class Loader(object):
def __init__(self, path, count):
'''
初始化加载器
path: 数据文件路径
count: 文件中的样本个数
'''
self.path = path
self.count = count
def get_file_content(self):
'''
读取文件内容
'''
f = open(self.path, 'rb')
content = f.read()
f.close()
return content
def to_int(self, byte):
'''
将unsigned byte字符转换为整数
'''
return struct.unpack('B', byte)[0]
# 图像数据加载器
class ImageLoader(Loader):
def get_picture(self, content, index):
'''
内部函数,从文件中获取图像
'''
start = index * 28 * 28 + 16
picture = []
for i in range(28):
picture.append([])
for j in range(28):
picture[i].append(self.to_int(content[start + i * 28 + j]))
return picture
def get_one_sample(self, picture):
'''
内部函数,将图像转化为样本的输入向量
'''
sample = []
for i in range(28):
for j in range(28):
sample.append(picture[i][j])
return sample
def load(self):
'''
加载数据文件,获得全部样本的输入向量
'''
content = self.get_file_content()
data_set = []
print 'image count:',self.count
for index in range(self.count):
data_set.append(self.get_one_sample(self.get_picture(content, index)))
return data_set
# 标签数据加载器
class LabelLoader(Loader):
def load(self):
'''
加载数据文件,获得全部样本的标签向量
'''
content = self.get_file_content()
labels = []
for index in range(self.count):
labels.append(self.norm(content[index + 8]))
#print 'labels:',labels
return labels
def norm(self, label):
'''
内部函数,将一个值转换为10维标签向量
'''
label_vec = []
label_value = self.to_int(label)
for i in range(10):
if i == label_value:
label_vec.append(0.9)
else:
label_vec.append(0.1)
return label_vec
def get_training_data_set():
'''
获得训练数据集
'''
image_loader = ImageLoader('train-images.idx3-ubyte', 60000)
label_loader = LabelLoader('train-labels.idx1-ubyte', 60000)
return image_loader.load(), label_loader.load()
def get_test_data_set():
'''
获得测试数据集
'''
image_loader = ImageLoader('t10k-images.idx3-ubyte', 10000)
label_loader = LabelLoader('t10k-labels.idx1-ubyte', 10000)
return image_loader.load(), label_loader.load()
def get_result(vec):
max_value_index = 0
max_value = 0
for i in range(len(vec)):
if vec[i] > max_value:
max_value = vec[i]
max_value_index = i
return max_value_index
def evaluate(network, test_data_set, test_labels):
error = 0
total = len(test_data_set)
for i in range(total):
label = get_result(test_labels[i])
predict = get_result(network.predict(test_data_set[i]))
if label != predict:
error += 1
return float(error) / float(total)
def train_and_evaluate():
last_error_ratio = 1.0
epoch = 0
train_data_set, train_labels = get_training_data_set()
print 'get train_data_set, train_labels...'
test_data_set, test_labels = get_test_data_set()
print 'get test_data_set, test_labels.....'
# 构建网络
network = fc.Network([784, 300, 10])
print 'get network:',network
train_labels, train_data_set=convert(train_labels, train_data_set)
test_labels,test_data_set =convert(test_labels,test_data_set)
while True:
epoch += 1
network.train(train_labels, train_data_set, 0.1, 1)
print '%s epoch %d finished' % (datetime.now(), epoch)
if epoch % 10 == 0:
error_ratio = evaluate(network, test_data_set, test_labels)
print '%s after epoch %d, error ratio is %f' % (datetime.now(), epoch, error_ratio)
if error_ratio > last_error_ratio:
break
else:
last_error_ratio = error_ratio
# 训练数据集和测试集的处理
def convert(train_labels, train_data_set):
trainlabels=[]
t1=np.shape(train_labels)
for i in range(len(train_labels)):
trainlabels.append(np.array(train_labels[i]).reshape(t1[1],1))
#print 'train_labels:',np.shape(trainlabels)
traindataset=[]
t2=np.shape(train_data_set)
for i in range(len(train_data_set)):
traindataset.append(np.array(train_data_set[i]).reshape(t2[1],1))
#print 'train_data_set:',np.shape(traindataset)
return trainlabels,traindataset
if __name__ == '__main__':
train_and_evaluate()运行结果:
image count: 60000
get train_data_set, train_labels...
image count: 10000
get test_data_set, test_labels.....
get network: fc.py:11: RuntimeWarning: overflow encountered in exp
return 1.0 / (1.0 + np.exp(-weighted_input))
at 0x7f3600119490>
2018-05-09 13:15:09.911136 epoch 1 finished
2018-05-09 13:16:06.405420 epoch 2 finished
2018-05-09 13:17:00.673801 epoch 3 finished
2018-05-09 13:17:52.530145 epoch 4 finished
2018-05-09 13:18:40.793027 epoch 5 finished
2018-05-09 13:19:27.942110 epoch 6 finished
2018-05-09 13:20:13.373169 epoch 7 finished
2018-05-09 13:21:00.198157 epoch 8 finished
2018-05-09 13:21:45.633917 epoch 9 finished
2018-05-09 13:22:31.279932 epoch 10 finished
2018-05-09 13:22:32.188052 after epoch 10, error ratio is 0.496400
2018-05-09 13:23:17.678800 epoch 11 finished
2018-05-09 13:24:03.042221 epoch 12 finished
2018-05-09 13:24:48.333277 epoch 13 finished
2018-05-09 13:25:33.668334 epoch 14 finished
2018-05-09 13:26:18.961969 epoch 15 finished
2018-05-09 13:27:04.220283 epoch 16 finished
2018-05-09 13:27:49.499477 epoch 17 finished
2018-05-09 13:28:34.895613 epoch 18 finished
2018-05-09 13:29:20.178684 epoch 19 finished
2018-05-09 13:30:05.451835 epoch 20 finished
2018-05-09 13:30:06.340205 after epoch 20, error ratio is 0.541500 这里有两个问题:
第一个问题:
- 运行中有一个exp的溢出警告,在网上查了下:一种是说numpy.exp返回值在float64中存储不下,会截取一部分,给出的是个wearing,这里认为不影响最终的结果。
- 另一种是同比缩小数值大小,以防止溢出。
第二个问题:
错误率比较大,所以说还要进一步的调参,这里只是提供一种思路。