一文看懂怎样用 Python 创建比特币交易
转自:区块链大本营
比特币价格的上上下下,始终撩动着每一个人无比关切的小心脏。从去年初的 800 美元左右,飞涨到去年底到 19783.21 美元最高点,不到1年,便有将近 25 倍的升值速度。尽管眼下又掉回 8000 多美元的价格,但价格差不多能搞出去年同期一个数量级,币圈人士“过去一年比以往 10 年挣的都多”,已经是不争的事实。
而对区块链开发者来说,据说也已经有拿到年新 500 万的天价。所以“跑步进入区块链”,已经成为不少程序员的共识。但是看过很多远离,我们如何才能迅速上手呢?国外网友 Ken Shirriff 在博客中分享了他在手动茶古剑比特币交易时的代码与对比特币协议的心得,区块链大本营编译如下。
近期,媒体行业对比特币表现出极大的热情,这鼓舞着我从网络底层的数据流开始,认真学习比特币的工作原理。通常人们会使用钱包软件来进行比特币交易,钱包软件在方便用户的同时,向用户隐藏了比特币的交易流程,而我想亲自动手来体验比特币交易,我的目标是用Python手动创建一笔比特币交易,以十六进制数据的形式将交易广播到比特币网络中,然后观察这笔交易是怎么被加入到区块链中的。事实证明,这个过程很有趣,希望你也对它感兴趣。
在本篇文章中,首先我会对比特币进行一个简单的概述,之后,我会从以下几个方面带领你们学习比特币:创建一个比特币地址(比特币中的账户),进行一笔比特币交易,签署交易,将交易广播到比特币网络中,最后等待交易的确认。
比特币简述:
首先,我会介绍一下比特币系统是怎么运转的,然后再深入探讨整个细节。比特币是一个基于点对点网络的电子货币,你可以用现金在网上购买比特币,用比特币向他人转账,在有些商家,你可以像使用支付宝一样使用比特币付款,当然,你也可以卖出所持有的比特币换回现金。
简而言之,在比特币网络中,分布式账本(区块链)记录并随时更新着每个比特币的所有权。与银行不同的是,比特币并没有与个人或个人的账户绑定,相反的,比特币只属于一个个比特币地址,比如:1KKKK6N21XKo48zWKuQKXdvSsCf95ibHFa。这里你可能已经绕晕了,难道这段字符中藏着比特币?当然不是,比特币地址是比特币网络中的一个身份,也可以通俗地说是你在比特币中开的一个“银行账户”,我们用这个“账户”来进行交易。在网站:blockchain.info中,你可以查到所有的交易信息:
但是怎么证明这个账户是我的呢,不急,先往下看,你的疑问我会为你一一解答。
比特币交易
如何像使用现金一样使用比特币呢?答案是创建一笔交易。在一笔交易中,比特币的所有者(上文提到过比特币的所有者是比特币地址)将所有权转移到一个新的比特币地址。比特币的一个颠覆性创新就是通过鼓励节点记账(也叫矿工挖矿),将交易记录放在一个分布式的数据库中。交易被集合在区块中,大概每十分钟比特币网络中产生一个新的区块,成为交易记录的一部分,称为区块链。加入到区块链中的交易可以被认为是一笔成功的交易。现在问题来了,谁来给你记账呢?是矿工,矿工的挖矿过程就是在往区块链中记账,矿工要核实每笔交易是否正确,核实完后,矿工们就开始算一道很难的数学题(密码学中的哈希函数),最早算出答案的人就能生成一个区块,也叫挖出了一个新的区块,这个区块将成为区块链的新一部分。
也许你会问了,明明是记账,干着会计的活,为什么要叫挖矿呢?和传统的在地下挖矿石一样,比特币挖矿也是会有收获的。挖矿是一种新发行比特币的过程,当前,每挖到一个矿,矿工会得到系统奖励的12.5个比特币,按目前一个比特币接近一万美元的市价,这就是一笔12.5万美元的巨款。此外,矿工还可以获得本区块中所有的交易费,举例来说,在高度为512587的区块中,幸运的矿工总共收获了12.829个比特币。正因如此,矿工之间的竞争十分激烈,采矿的难度与矿工间激烈的竞争是比特币安全的重要保证,因为这样可以保证没有坏人能操纵系统。
点对点网络
比特币并没有一个中央服务器,相反,比特币在一个点对点网络中运行。如果你运行一个比特币节点,那你就成了网络的一部分。比特币网络中的节点彼此交换自己存储的交易,区块,以及IP地址信息(用于节点间建立连接互相通信)。当你第一次连接到比特币网络,你的节点会从随机挑选的节点中下载区块链的信息。反过来,你的节点也会向后加入者提供信息。当你要创建一笔比特币交易时,你要把这笔交易发送给一些节点,这些节点会在比特币网络中广播这笔交易,直到全网都收到这笔交易。矿工们会收集你的交易信息,生成一个含有你这笔交易的区块,向全网广播,这时,你的节点也会收到这个区块信息,通过验证,这笔交易被加入到了区块链中,你就交易成功了。
加密技术
现在回到证明比特币账户是谁的这个问题。比特币使用数字签名技术以确保只有比特币账户的所有者才能使用账户中的比特币。比特币地址的所有者拥有与该地址相匹配的私钥,当花费比特币时,你用要这个私钥在交易上签名,证明自己是这个账户的所有者。这有点像现实生活中的盖章,盖章就意味着授权。怎么验证呢,公钥与比特币账户相关联,用公钥就可以验证签名是否正确。这样就解决了比特币账户是谁的这个问题。
怎么来区分不同的交易呢?交易和区块都使用密码学上的哈希值进行索引,是不是有点耳熟,对,在比特币协议中,多处使用到了哈希函数,矿工们刚才算的数学题就是在算哈希函数。
其实比特币并不长这个样
比特币协议探究
在接下来的文章里,我将逐步介绍我是怎样手动进行一次比特币交易的。首先,我生成了一个比特币账户以及对应的公钥,私钥。接下来我发起了一笔比特币交易,我向这个新生成的账户转了一小笔比特币。期间手动签署这笔交易很困难,它花费了我很多的时间。最后,我将这笔交易发送到比特币网络,等待它被加入区块链。本文的其余部分会详细地介绍这些步骤。
事实证明,手动进行比特币交易比我想象中的更加困难。正如你所看到的,比特币的协议有些许混乱:它使用了大端格式数字(高位编址,将高序字节存储在起始地址),小端格式数字(低位编址,将低序字节存储在起始位置),固定长度数字,可变长度数字,自定义编码格式,DER编码格式以及各种加密算法。因此,仅仅是将数据转换为正确的格式就浪费了很多时间。
我遇到的第二个难题就是加密,尝试一下手动加密,你就会发现密码学对人们多不友好,甚至可以说是无情。即使你只输错了一个字节,交易就会因出错被拒绝,而且它不会告诉你哪里出错了,你只能重来。
最后,手动签署交易的过程也比想象中难得多,签署交易时每个环节都必须零失误,要么又要退回重来。
比特币地址和密钥
第一步,我创建了一个比特币地址。通常情况下,人们都是使用比特币客户端软件来创建比特币地址和与之相关的密钥。本着学习的态度,我写了一些Python代码来生成比特币地址,从而揭示地址创建的机理。
比特币使用了一系列的密钥和地址,下图解释了它们的关系。首先你要创建一个随机的256位的私钥,这个私钥用于在花费比特币时签署交易。因此,私钥必须保密,否则你的比特币可能会被盗用。
椭圆曲线数字签名算法(Elliptic Curve Digital Signature Algorithm,ECDSA,美国政府的标准,接下来我们会讨论它)会从私钥中生成一个512位的公钥,这个公钥用于验证交易的签名。但不方便的是,比特币协议中需要在这个公钥上添加了前缀04,这个公钥在交易签署之前不会被泄露,不像其它系统中公钥就是为了公之于众的。
比特币地址与公钥的关系
下一步就是生成与他人交易时使用的比特币地址了。512位的公钥太长不方便使用,因此使用SHA-256和RIPEMD哈希算法将其缩小为160位。然后使用比特币定义的Base58Check 编码将密钥编码为ASCII(American Standard Code for Information Interchange,美国信息交换标准代码)格式。得到的地址(例如上文中的:1KKKK6N21XKo48zWKuQKXdvSsCf95ibHFa)就是你接收别人比特币时要发布的地址。需要注意的是,你无法从比特币地址中复原出公钥或私钥。如果你丢失了你的私钥(比如说你把私钥存在你的硬盘上,但硬盘丢失),你的比特币将永远丢失。
最后,钱包交换格式密钥(WIF)用于将私钥添加到你的钱包软件中,这只是将私钥进行Base58Check编码转换为ASCII格式,这一步是可逆的,而且很容易经过逆变换恢复出256位的私钥。(图中有我的私钥,我很好奇是否有人会用我的私钥去偷(通过私钥签署交易,从而转走)我那价值80美分的比特币,然而真有人那么做了,可以在
https://blockchain.info/address/1KKKK6N21XKo48zWKuQKXdvSsCf95ibHFa 看到,也算是为教学做贡献了。)
总之,共有三种密钥:私钥,公钥,公钥的哈希值,经过使用Base58Check编码,它们对外都是以ASCII格式表示。私钥是其中最重要的密钥,因为花费比特币时需要私钥签署交易,而且其他的密钥都可以从私钥中产生。公钥的哈希值就是你们刚看的的比特币地址。
我使用下面的代码片段来生成WIF格式的私钥和地址。私钥只是一个随机的256位的数字,使用椭圆曲线数字签名算法从私钥中生成公钥,公钥使用SHA-256算法,RIPEMD-160算法进行哈希计算,再经Base58编码并进行校验后得到比特币地址。最后,私钥用Base58Check编码以生成用于将私钥输入钱包软件的WIF编码。注意,这段Python随机函数代码在密码学上安全性并不高,如果你想要尝试这一步骤,建议使用更安全的钱包软件来生成比特币地址和密钥。
def privateKeyToWif(key_hex): return utils.base58CheckEncode(0x80, key_hex.decode('hex')) def privateKeyToPublicKey(s): sk = ecdsa.SigningKey.from_string(s.decode('hex'), curve=ecdsa.SECP256k1) vk = sk.verifying_key
return ('\04' + sk.verifying_key.to_string()).encode('hex')
def pubKeyToAddr(s): ripemd160 = hashlib.new('ripemd160') ripemd160.update(hashlib.sha256(s.decode('hex')).digest())
return utils.base58CheckEncode(0, ripemd160.digest())
def keyToAddr(s):
return pubKeyToAddr(privateKeyToPublicKey(s))
# Warning: this random function is not cryptographically strong and is just for example
private_key = ''.join(['%x' % random.randrange(16) for x in range(0, 64)])print keyUtils.privateKeyToWif(private_key)print keyUtils.keyToAddr(private_key)
keyUtils.py
从内部分析一笔交易
交易是比特币系统的基本操作,也许你会认为交易就是简单地把比特币从一个地址转移到另一个地址,但交易其实并不简单。一笔交易包含一个或多个输入和输出,交易中的每个输入的地址都提供比特币,每个输出的地址都接受比特币。
一笔简单的比特币交易,交易C花费了从交易A和交易B获得的0.008个比特币,其中0.001个比特币被当作交易费付给矿工
上图显示了一笔简单的比特币交易“C”,在这笔交易中,有0.005个比特币是在交易A中获得的,0.003个比特币是在交易B中获得的。(图中箭头是由新交易的输入指向得到这些比特币的交易的输出,所以比特币的流向是逆着箭头方向的。)对于输出,有0.003个比特币给了第一个比特币地址,有0.004个比特币给了第二个比特币地址,剩余的0.001个比特币作为交易费付给矿工。请注意,本次交易并没有影响到在交易A中另一个输出为0.015的比特币。
在一笔交易中,输入的比特币地址必须花出所有的比特币,假如你在之前的交易收到了100个比特币,但你只想花1个比特币,创建这笔交易你必须花完所有的100个比特币,那剩下的99个比特币怎么办呢?解决方案就是在交易中再增加一个输出,将剩余的99个比特币转给自己。这样你就可以花费任意数额的比特币。
通常交易要支付交易费,如果一笔交易中输入的比特币总和大于输出的比特币的总和,剩余的费用就是给矿工的交易费。这笔费用并没有明确要求,但是对于矿工而言,没有交易费的交易就会被列为低优先级交易,可能要等上几天才会被处理甚至被矿工直接丢弃。交易费通常并不高,但它可能影响着你的交易。
手动创建一笔交易
如下图所示,在我的实验中我发起了一笔只有一个输入一个输出的交易。我在Coinbase上买了一些比特币,并将0.00101234个比特币放入地址:
1MMMMSUb1piy2ufrSguNUdFmAcvqrQF8M5中,这笔交易哈希为:
81b4c832d70cb56ff957589752eb4125a4cab78a25a8fc52d6a09e5bd4404d48,我的目标是创建一笔交易,将这些比特币转入我的另一个地址:
1KKKK6N21XKo48zWKuQKXdvSsCf95ibHFa,扣除0.0001个比特币的交易费后,目标地址将获得0.00091234个比特币。
比特币交易结构实例
Blockchain.info上的交易记录
https://blockchain.info/address/1MMMMSUb1piy2ufrSguNUdFmAcvqrQF8M5?filter=4
按照协议标准,创建这笔交易很简单。如下表所示,这笔交易只有一个输入,源自于81b4c832d70cb56ff957589752eb4125a4cab78a25a8fc52d6a09e5bd4404d48中的输出0(第一个输出)。输出为0.00091234个比特币(91234在十六进制中用0x016462表示),它以小端格式存储在值区域中。加密过程中的scriptSig和scriptPubKey较为复杂,我们稍后再做讨论。
version |
01 00 00 00 |
|
input count |
01 |
|
input |
previous output hash(reversed) |
48 4d 40 d4 5b 9e a0 d6 52 fc a8 25 8a b7 ca a4 25 41 eb 52 97 58 57 f9 6f b5 0c d7 32 c8 b4 81 |
previous output index |
00 00 00 00 |
|
script length |
||
scriptSig |
script containing signature |
|
sequence |
ff ff ff ff |
|
output count |
01 |
|
output |
value |
62 64 01 00 00 00 00 00 |
script length |
||
scriptPubKey |
script containing destination address |
|
block lock time |
00 00 00 00 |
|
这是我生成交易使用的代码,这段代码只是把数据打包成二进制文件。签署交易较为困难,我们等一会儿再说。
# Makes a transaction from the inputs# outputs is a list of [redemptionSatoshis, outputScript]
def makeRawTransaction(outputTransactionHash, sourceIndex, scriptSig, outputs):
def makeOutput(data): redemptionSatoshis, outputScript = data
return (struct.pack("
return (
"01000000" + # 4 bytes version "01" + # varint for number of inputs outputTransactionHash.decode('hex')[::-1].encode('hex') + # reverse outputTransactionHash struct.pack('
"ffffffff" + # sequence "%02x" % len(outputs) + # number of outputs formattedOutputs +
"00000000" # lockTime
)
txnUtils.py
比特币交易怎样签署
下图为我们简单描述了交易是如何签署并相互连接的。针对中间这笔从比特币地址B转账到比特币地址C的交易。交易的内容(包括前一个交易的哈希值(索引))被进行哈希计算并用B的私钥签名。另外,B的公钥也被包含在了交易中。
通过执行几个简单运算,任何人都能验证B是否签署了这笔交易。首先,B的公钥与之前收到这笔比特币交易的地址做验证,证明B的公钥有效。(正如前面所说的,地址很容易从公钥中计算获得)。接下来,可以通过B的公钥验证B交易签名的真伪。这些步骤能确保交易的有效性和交易得到B的授权。比特币于众不同的一点是,B的公钥在B发起交易之前是不公开的。
在比特币系统中,比特币通过区块链上的一笔笔交易在不同的地址间传递。区块链上的每一笔交易都能被验证以确保比特币交易的有效性。
比特币交易的相互连接
比特币脚本语言
你可能会以为仅仅通过在交易内容中附上签名就可以签署比特币交易,其实不然,这个过程十分复杂。实际上,每一笔交易中都包含一个“小程序”,用于确认交易是否有效。这个“小程序”用脚本语言写成,通过这种基于堆栈的比特币脚本语言,我们可以应对许多复杂的比特币支付场景。例如,托管系统可以设定只要经过三分之二的用户授权,就可执行交易的规则,也可以设置其他的合约。
脚本语言十分复杂,大约有80种操作码,包括算数计算,按位操作,字符串处理,条件语句和堆栈操作。脚本语言也包含一些必要的密码学操作(SHA-256,RIPEMD等等)作为原语(原语是执行过程中不可被打断的基本操作,你可以理解为一段代码)。为了确保脚本语言可以运行完毕自动退出,该语言不支持任何循环操作,因此它不是图灵完备的。然而,实际上,它只支持少数类型的交易。
前一个交易中的脚本称为scriptPubKey,当前交易中的脚本称为scriptSig。要验证交易时,先执行scriptSig,然后再执行scriptPubKey。如果两个脚本都成功执行,交易就被认定为有效,交易中的比特币就可以成功花出。否则,交易无效。要注意的是前一个交易中的scriptPubKey规定了花费比特币的条件,当前交易的scriptSig必须满足这个条件。
在一个标准的交易中,scriptSig脚本将从私钥中生成的签名并压入堆栈中,再压入公钥。接下来scriptPubKey脚本会执行运算先验证公钥的有效性,再验证签名的有效性。
正如脚本中所表示,scriptSig:
PUSHDATA
signature data and SIGHASH_ALL
PUSHDATA
public key data
scriptPubKey:
OP_DUPOP_HASH160PUSHDATABitcoin address (public key hash)OP_EQUALVERIFYOP_CHECKSIG
当这段代码执行时,PUSHDATA操作首先会把签名压入堆栈,接着把公钥压入堆栈。OPHASH-160操作计算公钥的160位哈希值,PUSHDATA操作再把交易中的输入地址(输入账号)压入堆栈,然后,OP-EQUALVERIFY操作验证验证前两个堆栈中的值是否相等(验证这笔交易中你使用的比特币是否属于你自己)-如果公钥的哈希等于之前交易中的输出地址,这就证明公钥是有效的(证明这个比特币是你的)。最后,OP_CHECKSIG操作将检查交易的签名是否与堆栈里的公钥和签名匹配,匹配就证明签名是有效的(证明交易的到了你的授权)
签署交易
我发现签署这笔交易是手动使用比特币时最难的地方,这一过程出奇地困难且容易出错。签名的基本思想很简单,使用椭圆曲线签名算法和私钥来生成交易的数字签名,但细节非常棘手。签署交易的过程可以通过这19个步骤描述。
签署交易的19个步骤
对交易的签名让我面临巨大的挑战,这涉及到一个如何在交易内容中还没有加入签名时签署这笔交易的问题。为了避免这个问题,在计算生成签名之前,我把scriptPubKey这个脚本从上一笔交易复制到当前交易中(当前这笔交易正在被签署),然后将签名转换为脚本语言的代码,创建嵌入在当前交易中的scriptSig脚本。对于具有多个输入的交易,签署交易环节更加复杂,因为每个输入都需要单独的签名,这里我就不做详细讨论了。
哈希值这一步骤难倒了我。在签名之前,交易中有一个临时附加的哈希值常量。对于常规的交易,这个值是SIGHASH_ALL(0x00000001)。签名后,这个哈希值将从交易内容的最后删除,附加到scriptSig脚本中。
在比特币中另一件令人讨厌的事情是虽然签名和公钥都是512位的椭圆曲线值,但它们的表示方式完全不同:签名用DER编码方式编码,而公钥用纯字节表示。另外,两个值都有一个额外的字节,但位置并不一致:SIGHASH_ALL这个附加的哈希值常量放在签名后面,而04这个值放在公钥前面。
由于ECDSA算法需要使用随机数,所以调试签名十分困难。每次计算出的签名都会有所不同,因此无法与已知正确的签名进行比较。
正是由于上述的复杂性,我花了很长时间才得到了一个签名。不过,最终我找出了签名代码中所有的错误,并成功用它签署了一笔交易。这是我使用的签名代码:
def makeSignedTransaction(privateKey, outputTransactionHash, sourceIndex, scriptPubKey, outputs): myTxn_forSig = (makeRawTransaction(outputTransactionHash, sourceIndex, scriptPubKey, outputs) + "01000000") # hash code s256 = hashlib.sha256(hashlib.sha256(myTxn_forSig.decode('hex')).digest()).digest() sk = ecdsa.SigningKey.from_string(privateKey.decode('hex'), curve=ecdsa.SECP256k1) sig = sk.sign_digest(s256, sigencode=ecdsa.util.sigencode_der) + '\01' # 01 is hashtype pubKey = keyUtils.privateKeyToPublicKey(privateKey) scriptSig = utils.varstr(sig).encode('hex') + utils.varstr(pubKey.decode('hex')).encode('hex') signed_txn = makeRawTransaction(outputTransactionHash, sourceIndex, scriptSig, outputs) verifyTxnSignature(signed_txn)
return signed2_txn
txnUtils.py
最终的scriptSig脚本中包含签名以及比特币源地址的公钥(1MMMMSUb1piy2ufrSguNUdFmAcvqrQF8M5)。 这证明这笔交易有效,我可以花费这些比特币。
PUSHDATA 47 |
47 |
|
signature(DER) |
sequence |
30 |
length |
44 |
|
integer |
02 |
|
length |
20 |
|
X |
2c b2 65 bf 10 70 7b f4 93 46 c3 51 5d d3 d1 6f c4 54 61 8c 58 ec 0a 0f f4 48 a6 76 c5 4f f7 13 |
|
integer |
02 |
|
length |
20 |
|
Y |
6c 66 24 d7 62 a1 fc ef 46 18 28 4e ad 8f 08 67 8a c0 5b 13 c8 42 35 f1 65 4e 6a d1 68 23 3e 82 |
|
SIGHASH_ALL |
01 |
|
PUSHDATA 41 |
41 |
|
public key |
type |
04 |
X |
14 e3 01 b2 32 8f 17 44 2c 0b 83 10 d7 87 bf 3d 8a 40 4c fb d0 70 4f 13 5b 6a d4 b2 d3 ee 75 13 |
|
Y |
10 f9 81 92 6e 53 a6 e8 c3 9b d7 d3 fe fd 57 6c 54 3c ce 49 3c ba c0 63 88 f2 65 1d 1a ac bf cd |
|
最终的scriptPubKey脚本包含成功花费比特币时必须执行的脚本。需要注意的是,这个脚本将在未来花费这些比特币的时候执行。它包含以十六进制表示而不是以Base58Check表示的目标地址1KKKK6N21XKo48zWKuQKXdvSsCf95ibHFa,脚本的效果是只有这个目标地址的私钥所有者才能使用比特币,因此目标地址实际上是这些比特币的所有者
OP_DUP |
76 |
OP_HASH160 |
a9 |
PUSHDATA 14 |
14 |
public key hash |
c8 e9 09 96 c7 c6 08 0e e0 62 84 60 0c 68 4e d9 04 d1 4c 5c |
OP_EQUALVERIFY |
88 |
OP_CHECKSIG |
ac |
最终的交易
经过上述的一系列操作,我们完成了最终的交易。但是,别忘了,此时的交易还没加入区块链中,接收方还没有收到你的比特币。
privateKey = keyUtils.wifToPrivateKey("5HusYj2b2x4nroApgfvaSfKYZhRbKFH41bVyPooymbC6KfgSXdD") #1MMMM
signed_txn = txnUtils.makeSignedTransaction(privateKey,
"81b4c832d70cb56ff957589752eb4125a4cab78a25a8fc52d6a09e5bd4404d48", # output (prev) transaction hash 0, # sourceIndex
keyUtils.addrHashToScriptPubKey("1MMMMSUb1piy2ufrSguNUdFmAcvqrQF8M5"), [[91234, #satoshis
keyUtils.addrHashToScriptPubKey("1KKKK6N21XKo48zWKuQKXdvSsCf95ibHFa")]] ) txnUtils.verifyTxnSignature(signed_txn)
print'SIGNED TXN', signed_txn
makeTransaction.py
最终的交易信息如下所示:
version |
01 00 00 00 |
|
input count |
01 |
|
input |
previous output hash(reversed) |
48 4d 40 d4 5b 9e a0 d6 52 fc a8 25 8a b7 ca a4 25 41 eb 52 97 58 57 f9 6f b5 0c d7 32 c8 b4 81 |
previous output index |
00 00 00 00 |
|
script length |
8a |
|
scriptSig |
47 30 44 02 20 2c b2 65 bf 10 70 7b f4 93 46 c3 51 5d d3 d1 6f c4 54 61 8c 58 ec 0a 0f f4 48 a6 76 c5 4f f7 13 02 20 6c 66 24 d7 62 a1 fc ef 46 18 28 4e ad 8f 08 67 8a c0 5b 13 c8 42 35 f1 65 4e 6a d1 68 23 3e 82 01 41 04 14 e3 01 b2 32 8f 17 44 2c 0b 83 10 d7 87 bf 3d 8a 40 4c fb d0 70 4f 13 5b 6a d4 b2 d3 ee 75 13 10 f9 81 92 6e 53 a6 e8 c3 9b d7 d3 fe fd 57 6c 54 3c ce 49 3c ba c0 63 88 f2 65 1d 1a ac bf cd |
|
sequence |
ff ff ff ff |
|
output count |
01 |
|
output |
value |
62 64 01 00 00 00 00 00 |
script length |
19 |
|
scriptPubKey |
76 a9 14 c8 e9 09 96 c7 c6 08 0e e0 62 84 60 0c 68 4e d9 04 d1 4c 5c 88 ac |
|
block lock time |
00 00 00 00 |
|
小插曲:椭圆曲线签名
比特币的签名算法使用到了椭圆曲线签名算法,这么实用的功能,你可能会好奇它是怎么做到的?在当年英国数学家安德鲁·怀尔斯攻克费马大定理时,我第一次接触到了椭圆曲线的算法。椭圆曲线的数学思想很有意思,所以在这里我给大家做一个快速的概述。
椭圆曲线这个叫法令人迷惑,因为椭圆曲线并不是椭圆,而且看起来也不像椭圆,甚至椭圆曲线与椭圆相关性都很少。通俗地讲,椭圆曲线就是满足一个简单方程y ^ 2 = x ^ 3 + ax + b的曲线。比特币中使用的称为secp256k1的椭圆曲线,它满足的方程为y ^ 2 = x ^ 3 + 7。
secp256k1椭圆曲线
椭圆曲线的一个重要特性就是你可以用一个简单的规则来定义椭圆曲线上点的相加:如果在曲线上绘制一条直线,这条直线与曲线交与A,B,C三个点,那么这个加法定义为A+B+C=0。由这个加法的定义,我们可以定义整数乘法:例如4A = A + A + A + A。
为什么椭圆曲线在密码学上很有用?因为椭圆曲线做整数乘法运算速度很快,但做除法时需要蛮力。例如,你可以快速地计算一个乘法12345678*A = Q,但是如果你只知道A和Q,求解n*A=Q中的n十分困难。因此在椭圆曲线算法中,这里的12345678将是私钥,曲线上的点Q将是公钥。
在密码学中,点的坐标并不是它在曲线上的实值点,而是对整数的模数。椭圆曲线的一个好用的特性就是对实数或模数进行运算的数学运算几乎相同。正因为如此,比特币的椭圆曲线并不像上面的图片,而是一团杂乱无章的256位点集(想想在一个空间中充满了大量杂乱无章的点)。
椭圆曲线数字签名算法(ECDSA)接收交易的哈希值,使用该交易数据,私钥,以及一个随机数从椭圆曲线上生成一个新的点,从而实现对交易的签名。任何拥有公钥,交易数据,和签名的人都可以通过做一个简单的椭圆曲线运算来验证签名的有效性。读到这里,你应该明白了为什么只有拥有私钥的人才能签署消息,但拥有公钥的任何人都可以验证该消息。
把交易发送到比特币网络
回到交易中来,别忘了此时我们的交易还没有被加入到区块链中,还不是一笔有效交易。刚刚我创建并签署了一笔交易。下一步就是将这笔交易发送到比特币网络中,网络中的矿工会收集交易并把它打包进区块中。
如何找到比特币网络的节点
首先我要在比特币的点对点网络中找到一个节点。节点的列表会随节点的进出动态更新,当一个比特币节点连接到另一个节点时,它们就会不断交换彼此新发现的比特币节点信息,因此,新节点加入的消息会快速地传遍整个网络。
然而,新的比特币节点如何第一次找到比特币节点?这是一个先有鸡还是先有蛋的问题。比特币节点通过以下几种方法来解决这个问题。有几个可信的比特币节点会以bitseed.xf2.org的域名在DNS系统(Domain Name System,域名系统,万维网上作为域名和IP地址相互映射的一个分布式数据库)上注册,通过执行nslookup命令,你就可以得到这些节点的IP地址,只要有一个在工作即可。如果很不幸它们都没有工作的话,你可以试着连接那几个已经在你的客户端中硬编码记录下来的地址。
Nslookup命令可以用来寻找比特币节点
当用户启动或停止比特币客户端时,节点就会加入或离开比特币网络。所以连接节点有很大的不确定性,在我实验时,就遇到了连接的节点已经离开比特币网络的情况,如果你想重复我的实验,最好多找几个节点,可能需要多次尝试才能找到一个运行着的节点。
与比特币节点通信
一旦获得了一个正在工作的比特币节点的IP地址,当务之急就通过这个节点是把我的交易发送到比特币的点对点网络中。使用点对点的网络协议十分简单,我在端口8333上打开了一个到任意对等端的TCP连接,发送消息,然后接受反馈消息。比特币的点对点协议对用户很友好,即使我的请求数据出错时,还是继续与我保持通信。
重要提示:正如一些人指出的那样,如果你想重复我的实验,切记要使用比特币的测试网络,在测试网络上,你可以使用“虚拟”的比特币来进行交易。因为在真实网络上,万一你不小心,有可能会失去所有的比特币。还记得上面提到的那个100个比特币转账1个的交易么,如果你忘了将剩余的比特币转给自己,那么剩余的99个比特币就会作为交易费支付给矿工。但是本着科学的态度,我并不在意在真实的比特币网络中损失我这些价值1美元的比特币。
协议中包含24种不同的信息种类。每一条信息都是一个简单的二进制大对象(binary large object ,BLOB,是一个可以存储二进制文件的容器),其中包含一个ASCII命令和一个适用该命令的二进制有效参数。该协议可以在比特币的维基上查询。
连接到比特币网络的第一步就是通过交换客户端版本信息来建立连接。首先,我发送了一条客户端版本信息,其中包含我的协议版本号,IP地址和其他内容。比特币节点也向我回复了它的版本信息。在此之后,我应该回复一个verack信息(version acknowledgement,版本确认)来确认它的版本信息。正如我所说,比特币点对点网络协议对用户十分友好,即使我跳过了verack信息,之后的操作也是一切正常。
交换版本信息这一步并不简单,因为信息具有标准的格式,不过不用害怕,可以用几行代码来创建这些信息。下面代码段中的makeMessage函数可以由随机数,命令名以及命令的参数来生成一条消息。getVersionMessage函数通过将各个字段打包在一起来为版本消息创建参数。
magic = 0xd9b4bef9
def makeMessage(magic, command, payload): checksum =
hashlib.sha256(hashlib.sha256(payload).digest()).digest()[0:4]
return struct.pack('L12sL4s', magic, command, len(payload), checksum) + payload
def getVersionMsg():
version = 60002 services = 1 timestamp = int(time.time()) addr_me = utils.netaddr(socket.inet_aton("127.0.0.1"), 8333) addr_you = utils.netaddr(socket.inet_aton("127.0.0.1"), 8333) nonce = random.getrandbits(64) sub_version_num = utils.varstr('') start_height = 0 payload = struct.pack('
msgUtils.py
发送交易tx
我使用下面精简的Python代码把我的交易发送到比特币网络中,这个代码发送一条客户端版本信息,接受(也可以忽略)比特币节点的版本信息和verack信息。最后将我的交易以tx信息发送。代码中这个16进制的字符串是我之前创建的交易。
def getTxMsg(payload): return makeMessage(magic, 'tx', payload)sock = socket.socket(socket.AF_INET, socket.SOCK_STREAM)sock.connect(("97.88.151.164", 8333))sock.send(msgUtils.getVersionMsg())sock.recv(1000) # receive versionsock.recv(1000) # receive veracksock.send(msgUtils.getTxMsg("0100000001484d40d45b9ea0d652fca8258ab7caa42541eb52975857f96fb50cd732c8b481000000008a47304402202cb265bf10707bf49346c3515dd3d16fc454618c58ec0a0ff448a676c54ff71302206c6624d762a1fcef4618284ead8f08678ac05b13c84235f1654e6ad168233e8201410414e301b2328f17442c0b8310d787bf3d8a404cfbd0704f135b6ad4b2d3ee751310f981926e53a6e8c39bd7d3fefd576c543cce493cbac06388f2651d1aacbfcdffffffff0162640100000000001976a914c8e90996c7c6080ee06284600c684ed904d14c5c88ac00000000".decode('hex')))
minimalSendTxn.py
以下Wireshark(一个抓取,分析网络封包的软件)软件的截图显示出我是如何将交易发送到比特币网络中的。我用Python编写了脚本来分析网络数据,为了简单起见,在这里我使用Wireshark。从图中可以看到我的这笔tx交易。
Wireshark中抓取的这笔正在上传至比特币网络的交易tx
为了实时监控我这笔交易的进度,我在比特币网络中新运行了一个节点,在把我交易发到比特币网络5秒钟之后,另一个节点给我发送了这个tx消息,其中包含我刚刚发送的这笔交易的哈希,由此可见,在仅仅这几秒中,我的交易已经传遍了比特币网络,至少也是比特币网络的一部分。
交易成功:我的交易被加入区块链
在将我的交易发送比特币网络之后,我需要等待它被矿工开采出来加入到区块链中,然后才能宣称我的实验圆满成功。10分钟后,我的比特币节点收到一条含有新区块信息的inv消息(参见下图Wireshark抓到的网络封包),检查这个区块后发现我的交易被包含在了区块中,证明我的交易是有效的,我的实验成功了。通过我的比特币钱包软件和在线查询,再一次确认了我已经交易成功。可以说,经过不断的努力,我成功手动创建了一笔交易,并让比特币系统接受了它。(当然了,我也经过了几次失败的尝试,这些错误的交易都消失在了网络之中,永远都不会被检索到。
Wireshark中抓取的新区块产生的封包信息
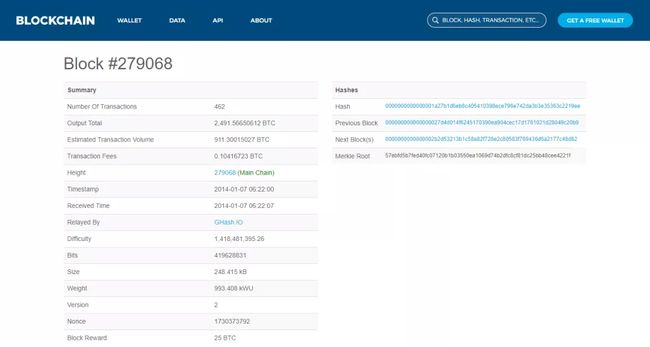
我的交易是被当时哈希算力(挖矿速度)最大的矿池(多个矿工一起挖矿)GHash.IO挖出,区块高度为279068,区块哈希为0000000000000001a27b1d6eb8c405410398ece796e742da3b3e35363c2219ee,在上图Wireshark数据包中inv消息的哈希值是经前后反转得到的ee192……。你应该会发现区块的哈希值以大量的0开头,在一个16进制的哈希值中发现一个以这么多0开头的数,这就是为什么挖矿如此困难的原因。这个区块中由462笔交易,我的交易是其中之一。
高度为279068的区块以及我发起的这笔交易
(https://blockchain.info/block-index/341440/0000000000000001a27b1d6eb8c405410398ece796e742da3b3e35363c2219ee)
挖到这个区块的矿工们收到了25个比特币的奖励,交易费总共是0.104个比特币,按当时的市价分别为19000美元和80美元。我支付了0.0001个比特币的交易费,大约是我交易额的10%,按当时的市价为8美分。
结论
手动进行比特币交易比我想象中困难得多,但是在这个过程中我学到了很多,希望你也是。我的Python代码仅仅是为了介绍,如果你想跟我一样用Python手动进行比特币交易,也可以试试这几个项目。
https://en.bitcoin.it/wiki/Bitcoin-python
https://github.com/richardkiss/pycoin
https://github.com/jgarzik/python-bitcoinlib