2D基本图形的Sign Distance Function (SDF)详解（上）

前言

符号距离函数（sign distancefunction），简称SDF，又可以称为定向距离函数（oriented distance function），在空间中的一个有限区域上确定一个点到区域边界的距离并同时对距离的符号进行定义：点在区域边界内部为正，外部为负，位于边界上时为0。

  SDF在光线追踪领域有很重要的应用。实际上写这篇博客是受到了 闫令琪 大神的课程B站视频-GAMES101-现代计算机图形学入门的影响，他在课程中分享了一个神奇的网站 Shadertoy ， 并且将另一位大神 inigo quilez 的作品进行了展示，为我打开了一扇新世界的大门。实际上你能在iq大神自己写的文章：raymarching distance fields，中看到他利用raymarching技术生成的许多精美的图像。这里不得不再次表达对shadertoy网站感激之情，这个网站伟大的地方就在于你能从中完完整整地看到那些绚丽夺目的特效背后的代码，并且你可以对它们进行修改然后实时编译查看效果，这一切仅需要你有一点GLSL语言基础以及一定的数学能力（数学令人头大），好在主要是几何学的知识。
  咳咳扯远了，iq大神也提到，SDF在raymarching发挥了重要作用，因此他自己也有两篇博客分别列出了2D以及3D基本图形的SDF，问题就在于iq大神这个人吧，一看他就是大神，代码写得都那么简洁凝练，追求高效。能不写if分支就绝不写，能一个语句处理五种复杂情况就绝不写哪怕一句多余的话。这样的代码确实看起来短小精悍优美，但是在缺乏注释的情况下对于阅读者学习者来说可就是一种折磨了。因此本文实际上就是对其中的2D篇中各个函数的注释和分析，代码不是我写的（我也写不出(lll￢ω￢)），光是看懂就耗费了很长的时间了。
  另外，如果您对计算机图形学方向不感兴趣甚至根本就不是程序员出身，那本文抛开代码也会提及纯数学意义上的“如何计算平面上任意一点到一个给定图形之间的最短距离”这个问题，希望对您有所帮助O(∩_∩)O
  废话不多说，让我们开始吧！

实践出真知

  希望您在阅读本文时，可以同时打开这篇文章：2D distance functions, 并且打开iq大神在每个函数后面对应在shadertoy网站上面的实现，这样直观地感受到每一条语句它所发挥的实际作用，您可以动态调整某些数据以观察其改变，这样能帮您更好地理解该函数的实现思路。当然，手边的纸笔在理解数学意义上或许能带来更大的帮助。

 

基础2D图形的SDF

1. 圆形

代码：（注：代码中传入的参数p在每个函数中都表示需要计算最短距离的平面上的任意一点）

/**
* 圆形：  1. 原点位于中心点
*        2. r表示半径
*/
float sdCircle( vec2 p, float r )
{
  // 与圆心距离位r的点，在该圆上，SDF取值0
  return length(p) - r;
}

  圆形几乎是最简单的2D图形了，它的定义就是与圆心的距离等于半径的所有点的集合。接下来我们会经常见到下面这种风格的图片，实际上他就是iq大神在展示自己的2D距离函数的效果，我们可以看到白色的线条连起来的就是和目标图形距离为0的点，也就是在图形上的点。而蓝白色就是图形内部点，与图形的最短距离为负数，外面黑黄的部分则是图形外部的点，距离为正。每一个封闭的圈都是一条等距离线。
 
 

2.线段

代码：

/**
* 线段：  1. a，b表示线段两个端点的坐标
*/
float sdSegment( in vec2 p, in vec2 a, in vec2 b )
{
    // pa表示a点指向p点的向量， ba表示a点指向b点的向量
    vec2 pa = p-a, ba = b-a;
    // h表示pa在ba上投影的长度占ba长度的比例，限定到[0,1]
    float h = clamp( dot(pa,ba)/dot(ba,ba), 0.0, 1.0 );
    // ba*h 是以a为起点，方向与ba相同，长度等于pa在ba方向上投影的长度的向量
    // pa视为斜边，ba*h是直角边，那么pa - ba*h则是另一条直角边，也就是从p点做垂线垂直于ab，显然该垂线的长度就是所求最短距离
    return length( pa - ba*h );
}

  实际上虽然线段看起来简单，但他确实接下来大多数图形距离函数的基础，因为总有一些图形它拥有一条直边，那时计算最短距离时肯定要求p点到某一条线段的距离。那么我们现在来解释一下，对于任意一条线段，我们可以按照下面这样把它所在的平面划分为三个区域，边界就是两条过两个端点垂直于线段的直线，划分的标准是什么呢？就是平面内任意点P在区域1内时，线段AB上与它最短的距离点（暂且称为C点）始终是A点，最短距离的长度是|AP|，或者说，长度可以写成|AP - AC|。区域3也是同样，点C始终是B点，长度是|AP - AB|或者写成|AP - AC|。而在区域2内很显然，是c点，也就是点p在ab方向上的投影，最短距离是|AP - AC|。行了，我们将三个区域的表示方法统一了（实际上这是iq大神的惯用手段）。
  确定AC是什么很关键，从下图看很容易知道其实AC就是AB乘一个系数得到的，p点在在区域1时该系数始终是0，区域3内时该系数是1，区域2内该系数就是AP在AB上的投影占AB的比例，这其实就是clamp函数的作用了。剩下的其实就不难理解，我觉得关于线段的SDF这一个函数应该算是iq大神写的比较容易理解的代码，其他地方他会直接把第二和第三句合在一起写（心累）。之所以这里要啰嗦这么多，完全是为了给下面其他的几何图形打基础，因为这个逻辑会经常出现，clamp函数也会经常出场的。
 

  最终结果如下图，这里又得啰嗦几句了，大家观察下图白线外面的圈像什么？实际上就是胶囊体。线段的SDF结果只要再减去一个常数就可以得到一个胶囊体，这个神奇的特性下面会分析。
 
 

3. 长方形

代码：

/**
* 长方形 box：  1. 原点位于长方形的中心点，形状是轴对称的
* 				2. b表示长方形右上角顶点的坐标
*/
float sdBox( in vec2 p, in vec2 b )
{
    // abs(p)是常用技巧，由于该图形四个象限都是相同的，因此都映射到第一象限即可
    // 现在的d表示长方体右上角顶点直线p点的向量
    vec2 d = abs(p)-b;
    // p点在外部：length(max(d,0.0)), 在内部则是min(max(d.x,d.y),0.0), 这两项总至少有一项为0
    return length(max(d,0.0)) + min(max(d.x,d.y),0.0);
}

  同样的思路，我们将依据图形上与P点最短距离位置点选择的不同，将第一象限划分（其他象限都映射到第一象限即可）四个区域，其中三个属于长方形外部，一个属于内部。我们先来看看外部的SDF怎么计算，观察下图我们可以看到代码中的d其实就是四条红色的向量（区域1内的和绿色向量重叠了），落在区域2内的点距离函数取d.y即可，因为d.x是负数，落在区域4内的点取d.x，因为d.y是负数，负数就表示你在那一个方向上处于长方形的“内部”，若两个分量都是正数，那就取|d|即可。三种情况统一到一句代码length(max(d, 0.0))里面了。
  看长方形内部的点，也就是区域3，此时的d两个分量都是负数，那只要选择绝对值小的那个分量即可（绿色的向量），即max(d.x, d.y))。那加个min()是什么意思呢？还不是因为iq大神想要把这四个区域的判定都挤压在一条语句内完成嘛~
 

 
   再次注意观察下面的图形，如果我们想要得到一个圆角的长方形的SDF该怎么做呢？没错，只需要将普通长方形的SDF结果减去一个常数，也就是圆角的半径即可。你看白圈外面的等高线不就是一个带圆角的长方形吗？
 

 

4. 菱形

代码：

/**
* 菱形：  1. 原点在菱形的中心点，四个顶点都在坐标轴上
*         2. b.x = 与x轴正半轴交点， b.y = 与y轴正半轴交点
*/
float ndot(vec2 a, vec2 b ) { return a.x*b.x - a.y*b.y; }
float sdRhombus( in vec2 p, in vec2 b)
{
    vec2 q = abs(p);  // 坐标轴对称
    // 计算的是线段b的中点到p点的向量，在b上的投影限制到[-1, 1]
    // 负数表示向量偏向于y轴， 正数表示偏向x轴
    float h = clamp((-2.0*ndot(q,b)+ndot(b,b))/dot(b,b),-1.0, 1.0);
    /* 实际上h从-1到1的滑动过程，[0.5*b*vec2(1.0-h,1.0+h)] 表示一条从原点出发，
       终点在向量b上由左上到右下的滑动的向量 */
    float d = length( q - 0.5*b*vec2(1.0-h,1.0+h) );
    // 符号：可计算(b.x, -b.y)和(p.x, p.y-b.y)的叉积，得两向量的相对位置
    return d * sign( q.x*b.y + q.y*b.x - b.x*b.y );
}

  这个函数可能乍一看会让人懵逼，实际上我也觉得有点过于复杂且没必要了。它的核心思想其实还是和上面的线段的SDF一模一样，但是在线段的SDF中，我们是选取了线段的一个端点和目标点P进行连线然后投影，但是在这里iq大神不选择端点了，选择了一个中点，然后继续投影，那我们知道现在就不应该再限制在[0, 1]，而是[-1, 1]，为了处理选择中点带来的影响，下一句计算d时也得进行一步看上去比较绕的操作，不过核心思路没变，那就是当P点在区域1是，P点的投影点应该固定为A点是吧，我们来看看0.5*b*vec2(1.0-h,1.0+h)，当h取-1时，这句表达式确实得到A点坐标，那就行了。区域3同理。至于符号的计算，可以计算P和某一端点（代码里选择了A点）的连线，然后看OP在AP的左边还是右边即可，使用叉积的正负可以用来判断。最终化简结果就像return后面代码写的那样。
  可能有些同学一开始会疑惑定义的ndot函数的几何意义，起码在这里它没表现出什么特殊的几何意义，如果你手算公式，会发现那仅仅是一个简化后的运算结果而已。真要说它有什么几何意义其实也有，下文中“一般三角形”的部分会做讨论。
 

 
我自己使用前面的线段SDF思路写了一个菱形的简单实现，思路可能更清晰一点，结果是一样的：

float sdRhombus( in vec2 p, in vec2 b)
{
	// 参考线段的SDF
    vec2 a = vec2(0, b.y); // 与y轴交点
    vec2 c = vec2(b.x, 0);
    vec2 pa = q-a, ba = c-a;
    float h = clamp( dot(pa,ba)/dot(ba,ba), 0.0, 1.0 );
    float d = length( pa - ba*h );
    return d * sign( q.x*b.y + q.y*b.x - b.x*b.y );
}

 

5. 等边三角形

代码：

/**
 * 等边三角形：  1. 原点在三角形中心点
 *              2. r表示边长的一半（不是中心点到顶点的距离）
*/
float sdEquilateralTriangle(in vec2 p, in float r )
{
    const float k = sqrt(3.0);
    p.x = abs(p.x);
    // 由于三角形可以看成是由三个部分绕中心点三个角度生成的，x负半轴不用考虑
    // 所以只需要考虑在区域 1的那部分，这一部分可以通过关于直线y=-1/sqrt(3)*x对称映射到下方的三分之一
    // 映射关系如下：
    if( p.x+k*p.y>0.0 ) p=vec2(p.x-k*p.y,-k*p.x-p.y)/2.0;
    // 一切都归一到只需要看区域 2-3-4即可
    // x在减去r后，若其值-2*r
    // 否则，需要原x轴坐标减去左/右下角坐标x值
    p.x -= r;
    p.y += r/k;
    p.x -= clamp( p.x, -2.0*r, 0.0 );
    return -length(p)*sign(p.y);
}

   首先提一句，对于这些正多边形，后面会给出比较通用的一个函数来处理。这里单把正三角拿出来可能是为了图一乐（），性能上的差异应该很小吧。废话不多说，我们看到一个关于y轴对称的图形，一句p.x = abs(p.x)肯定是免不了的，实际上映射这个技巧会在这个函数以及后面的函数中发挥巨大的作用。我们该怎么理解这种映射呢？关于对称轴是坐标轴的对称我们都很容易理解，但是如果对称轴不是坐标轴，或者甚至这种映射不是对称，而是旋转、缩放什么的呢？这里有必要讨论一下：

映射

• 为什么需要坐标映射？ 答：我们想要降低问题的复杂度，如果有一块区域的坐标比较容易计算，那么其他区域的坐标可以映射到该区域来计算。 *
• 什么样的图形可以使用坐标映射？ 答：图形具有一定的规律形，一般来讲它可以是轴对称的或者中心对称的，我们可以按某种方式将图形划分成完全相同的若干个小块，且其中有一块计算SDF较为便捷。
• 代码中怎么理解坐标映射？ 答：代码里的映射模块就像一道闸，各式各样的坐标进去，转化到同样的范围后再放出来。如果有哪块区域进去之前和出来之后没有发生变化，那么它就是天之骄子，后面的代码全都是为它而准备的。而且闸有可能不止一道噢，有点坐标在经过一道闸之后就下车了到达目的地了，有的还得再继续转换。这点在正三角形，正五边形里大家就会体验到。

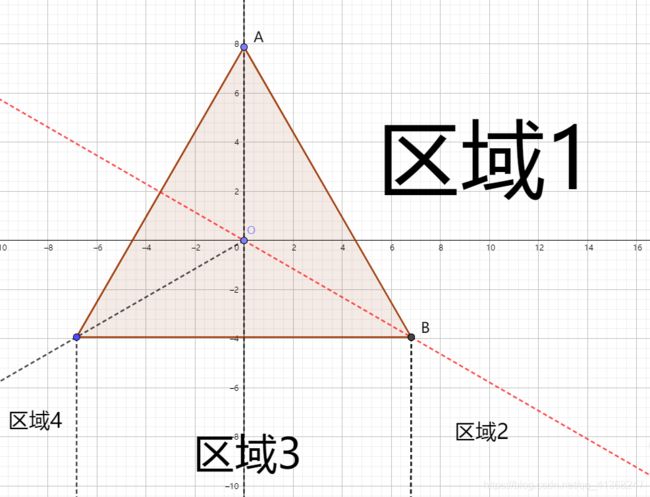
   又跑远了，回到正三角形。首先它是关于Y轴对称的图形。其次，它还是一个关于下图红线对称的图形。如此规则的图形肯定要映射（不映射也可以，前面都学会计算点到线段的SDF了，依次计算点到三条边的距离然后取最小值不行吗？当然可以但这不是iq大神的作风！），先问映射到哪里呢？毫无疑问是到区域2-3-4,因为计算这些区域内的点的SDF就是计算到一条平行于x轴的线段的距离，这是最简便的（相较于计算斜边来说）。那行，咋映射先放一边，区域2-3-4里面的点的SDF怎么计算呢？相信前面有认真思考的同学会脱口而出：连接PB, 计算和水平边的投影，限制在某个范围里，再用OP减……对对对，就是这么个套路，这里就不重复啰嗦了。那就看看咋映射呗，其实直接关于红线对称就完事了。注释我都写在代码里了，如果还是有疑惑可以看我下面的改写。至于对称关系为什么是p = vec2(p.x-k*p.y, -k*p.x-p.y)/2.0;手算一下即可。
(PS: 如果你看了iq大神的原代码，会发现我将p.x-=r; p.y+=r/k;两句提到了映射操作的后面进行，由于这两句表示的是沿着对称轴的平移，所以在映射前还是后进行是没有区别的，我认为放在后面更容易理解~)
 

改写程序：

float sdEquilateralTriangle(in vec2 p, in float r )
	const float k = sqrt(3.0);
	// 左右对称
    p.x = abs(p.x); 
    // 如果你在区域1，就取映射
    if( p.x+k*p.y>0.0 ) { 	
    	p=vec2(p.x-k*p.y,-k*p.x-p.y)/2.0; // 映射，即关于红线对称
    }
    if(p.x>r) p.x -= r; 		   // 对称后在区域 4？
    else if(p.x<-r) p.x -= (-r);   // 你在区域 2？ 
    else p.x=0.0;  // 噢，在区域 3啊，那x轴抹掉就行啦
    p.y += r/k;    // 注意r表示边长的一半
    return length(p)*sign(-p.y);
}

 

6. 等腰三角形

代码：

/**
* 等腰三角形：  1. 原点位于顶角，垂直于底边的高和y轴重合
*              2. q表示右腰的向量，一般q.y为负（此时顶角是朝上的）
*/
float sdTriangleIsosceles( in vec2 p, in vec2 q )
{
    p.x = abs(p.x);
    // 分为两种可能的最小距离： 1.与腰的距离， 2.与底的距离
    // 1. 与腰
    vec2 a = p - q*clamp( dot(p,q)/dot(q,q), 0.0, 1.0 );
    // 2. 与底
    vec2 b = p - q*vec2( clamp( p.x/q.x, 0.0, 1.0 ), 1.0 );
    float k = sign( q.y );
    float d = min(dot( a, a ), dot( b, b ));
    float s = max(k*(p.x*q.y-p.y*q.x), k*(p.y-q.y)); // 两项都小于零才是取负，即内部
    // float s = k*(p.y-q.y)>0.0?((k*(p.x*q.y-p.y*q.x))>0.0?1.0:-1.0):-1.0; // 可用此句替换
	return sqrt(d)*sign(s);
}

  这里其实都不用我画图了，思路很清晰。首先这是个Y轴对称的图形，然后我们分别计算和点P与腰和底的距离，取最小值就好了。可能需要注意的是符号怎么计算，过程是：如果点P被底认证为内部，同时也被腰认证为内部，那才是真正的在内部。这里用到的也是叉乘，来判断OP在底/腰的左边还是右边。这里iq大神写的也是很容易让人理解（好歹把d单独拎出来了）
 

 

7. 一般三角形

代码：

/**
* 一般三角形：  1. 原点不限
*              2. 三条边的向量都给出，为 p0,p1,p2
*/
float sdTriangle( in vec2 p, in vec2 p0, in vec2 p1, in vec2 p2 )
{
    vec2 e0 = p1-p0, e1 = p2-p1, e2 = p0-p2;
    vec2 v0 = p -p0, v1 = p -p1, v2 = p -p2;
    // 分别计算过p点垂直于三条边的向量，箭头指向p点
    vec2 pq0 = v0 - e0*clamp( dot(v0,e0)/dot(e0,e0), 0.0, 1.0 );
    vec2 pq1 = v1 - e1*clamp( dot(v1,e1)/dot(e1,e1), 0.0, 1.0 );
    vec2 pq2 = v2 - e2*clamp( dot(v2,e2)/dot(e2,e2), 0.0, 1.0 );
    // 由于不清楚传入的三个点是顺时针还是逆时针顺序，先确定好基本符号
    // 若s是-1，说明传入是逆时针
    // 假设规定传入都是顺时针顺序，则s为1，可无视
    float s = sign( e0.x*e2.y - e0.y*e2.x );
    // 这里的 d并非具有什么实际几何意义的向量，而是作为一个数据的集合来使用
    // 它的第一个分量d.x表示p点与各边长度的平方中的最小值，它的第二个分量可以用来判断内部外部
    // 假如点P在三角形内部，那么参与比较的三个式子都会是正数，它们中的最小值也将是正数
    // 若在外部，则至少有一个式子是负的，取最小值后d.y也将是负值
    vec2 d = min(min(vec2(dot(pq0,pq0), s*(v0.x*e0.y-v0.y*e0.x)),
                     vec2(dot(pq1,pq1), s*(v1.x*e1.y-v1.y*e1.x))),
                     vec2(dot(pq2,pq2), s*(v2.x*e2.y-v2.y*e2.x)));
    // 若d.y为负数，说明在三角形外，不要漏看下面一行的负号
    return -sqrt(d.x)*sign(d.y);
}

  逻辑也不是很难理解，但是我们可以看到这里有一个运算发挥着至关重要的作用，那就是二维向量的叉乘。

float cross(vec2 a, vec2 b) { return a.x*b.y - a.y*b.x; }

  看起来结果是个标量，其实叉乘的是矢量，上面的函数得到的只是它的模长，而且还是带符号的。符号哪里来的呢？叉乘的运算公式是：|a||b|sinθ，这里sinθ的正负其实就和向量a, b的相对位置有关了（点乘的结果和相对位置无关是因为cos(θ)==cos(-θ)）。实际上，若a向量逆时针旋转得到b向量所在的方向 / a向量在b向量的左边 都能得到：cross(a, b)>0，反之亦然，也能从cross的结果回推两向量的相对位置。这个运算十分重要，会多次出现。特别地，有时候你可能会看到这样的公式：

float ndot(vec2 a, vec2 b ) { return a.x*b.x - a.y*b.y; }

  感觉很奇怪，既不像叉乘也不像点乘。其实它也有几何意义，我们知道向量(x, y)的两条垂直于它的向量分别是(y, -x)和(-y, x)，或者说，(y, -x)是(x, y)逆时针旋转90°得到的，(-y, x)是(x, y)逆时针旋转90°得到的。那么现在应该看出来了，上面的式子就是a和垂直于b的向量(b.y, -b.x)做叉乘。

 

8. 不均匀的胶囊形

代码：

/**
* y轴对称的不均匀胶囊  1. 下半圆的圆心为原点
*                       2. h表示两个半圆的圆心之间的距离, ra为下半圆半径
*/
float cro(in vec2 a, in vec2 b ) { return a.x*b.y - a.y*b.x; }
float sdUnevenCapsuleY( in vec2 p, in float ra, in float rb, in float h )
{
	p.x = abs(p.x); // 左右对称
    float cos_h = (ra-rb)/h;
    float sin_h = sqrt(1.0-cos_h*cos_h);
    // c是垂直于直线边的单位向量，直线边单位向量为(-cos_h, sin_h)
    vec2  c = vec2(sin_h, cos_h);
    // 所谓cro其实可以看成先将b逆时针旋转90°，然后再计算a和b的点乘
    // 胶囊的sdf计算同样分为三部分，上半圆+直线边+下半圆， 方法是将op向量投影到直线边上
    // 所以k就表示op投影到直线边上，可以用来判断p点处于哪块区域
    float k = cro(c,p);
    // m表示op投影到直线边逆时针旋转了90°的向量上，可用来计算p点与下圆圆心之间的距离
    float m = dot(c,p);
    // op长度的平方
    float n = dot(p,p);

    if( k < 0.0)    return sqrt(n)- ra;  // 位于下圆部分
     // 上圆，这里用到了余弦定理，h表示两圆心的长度，以及op和p点到上半圆的连线组成一个三角形，sqrt(n)*cos(op与y轴夹角)=p.y （因为h在y轴上）
    else if( k > c.x*h )    return sqrt(n+h*h-2.0*h*p.y)- rb;
    // 减去ra
    else    return m - ra;
}

  下图中绿色的线条表示最短距离向量。其实只要把区域划分出来，整个代码的核心思路就可以把握住了。
  区域1内的P点与上圆心距离最近，区域3内的点与下圆心距离近，区域2内的点与直线边距离最近。那么我们可以故技重施，计算op在直线边上的投影，然后又是压缩到某个范围就行了。实际上也是这么做的，但是代码又一次试图把我们绕进去。为了简短iq大神费劲了心机来整读者。我们看上面代码里面的c，其实就是下图中紫色线段方向上的单位向量，它的方向有很多种“身份”，是右直线边的垂直方向，同时也可以说成是下方圆的右边界的方向，自然dot(c,p)就是OP在c上投影的长度，那么cro(c,p)又是什么鬼？叉乘？如果我们把叉乘理解为与垂直于C的单位向量（也就是下图中的C⊥）的点乘那么就好理解了。你会发现又绕回来了，C⊥不就是刚才说的直线边所在方向的向量单位嘛？确实如此。那么k就可以用来判断点P所处的区域，由于C⊥是单位向量，所以不能限制在[0, 1]，应该限制在[0, 直线边长度]，也就是[0, c.x\*h]。那m可以用来干什么？其实就是计算区域2时，将p点投影到下图两条用来划分的平行线里面下方的那条上，然后之间减去下圆的半径就行了。投影到上方的平行线也可以但是麻烦一点点。这下子知道为什么要绕一大圈搞出C和C⊥了吧。( •̀ ω •́ )✧另外，位于区域1的点可以使用余弦定理来求出。
  


  

9. 任意位置的不均匀的胶囊形

代码：

/**
 * 普通的不均匀胶囊  1. 原点不固定
 *                  2. pa,pb表示两圆心坐标， ra,rb表示两圆半径
*/
float sdUnevenCapsule1( in vec2 p, in vec2 pa, in vec2 pb, in float ra, in float rb )
{
    // 思路是坐标转化，将问题转化成y轴对称的胶囊
    // 预计算
    pb -= pa; 						// pa指向pb的向量
    float h = sqrt(dot(pb,pb));     // 两圆心距离
    
    // 1. 坐标平移：以pa作为原点的平移，相当于将胶囊的一个圆心平移到原点
    p  -= pa;   
    // 2. 坐标旋转：p.x = p.x* pb.y/h - p.y* pb.x/h
    //             p.y = p.x* pb.x/h + p.y* pb.y/h
    // 			实际上pb/h就是单位向量，其x分量就是cosθ,y分量就是sinθ
    // 			要将圆心连线旋转到与y轴平行，也就是逆时针旋转90-θ度，θ是连线与x轴夹角
    /*	
    	左乘旋转矩阵：
        [cos(90-θ), -sin(90-θ)]         [sinθ,  -cosθ]       [pb.y, -pb.x]
        [sin(90-θ),  cos(90-θ)]     =   [cosθ,   sinθ]  =    [pb.x,  pb.y]
    */
    vec2  q = vec2( dot(p,vec2(pb.y,-pb.x)), dot(p,pb))/h;
    
    // 调用Y轴对称版本 -----------
    return sdUnevenCapsuleY(q, ra, rb, h);
}

  举这个例子其实不只是单纯想说胶囊形，而且对于任何的其他位置不那么特殊的图形，都可以用先平移再旋转（需要的话还有放缩），然后就可以应用这些SDF函数了。之所以刚好是在胶囊形做这样的示范，其实没有什么理由。总结一下：

• 平移：前面（以及后面）给出的SDF都有指定坐标轴原点在图形的哪个位置，你只需要事先找出该点，然后接下来所有的P点都减去该点坐标即可。
• 旋转：除了指定原点的位置，这些SDF都有默认图形摆放的方向，先找到角度，然后乘一个旋转矩阵即可。
   
  
    有点长了，剩下的下一篇接着分析吧。
     2D基本图形的Sign Distance Function (SDF)详解（下）