抛物线法、牛顿法、弦截法求根实例
计算方法第四次计算实习题
7.用下列方法求 f ( x ) = x 3 − 3 x − 1 = 0 在 x 0 = 2 附 近 的 根 , 根 的 准 确 值 x ∗ = 1.87938524.. , 要 求 计 算 结 果 准 确 到 四 位 有 效 数 字 f(x)=x^3-3x-1=0在x_0=2附近的根,根的准确值x^{*}=1.87938524..,要求计算结果准确到四位有效数字 f(x)=x3−3x−1=0在x0=2附近的根,根的准确值x∗=1.87938524..,要求计算结果准确到四位有效数字
(1)用牛顿法
(2)用弦截法,取 x 0 = 2 , x 1 = 1.9 x_0=2,x_1=1.9 x0=2,x1=1.9
(3)用抛物线法,取 x 0 = 1 , x 1 = 3 , x 2 = 2 x_0=1,x_1=3,x_2=2 x0=1,x1=3,x2=2
解题思路:按部就班,套公式编写程序即可注意控制精度,要求准确到四位有效数字,即要求准确解和所得近似解误差不超过 0.5 ∗ 1 0 − 4 0.5*10^{-4} 0.5∗10−4,同时要注意迭代时的变量关系,以下是源代码:
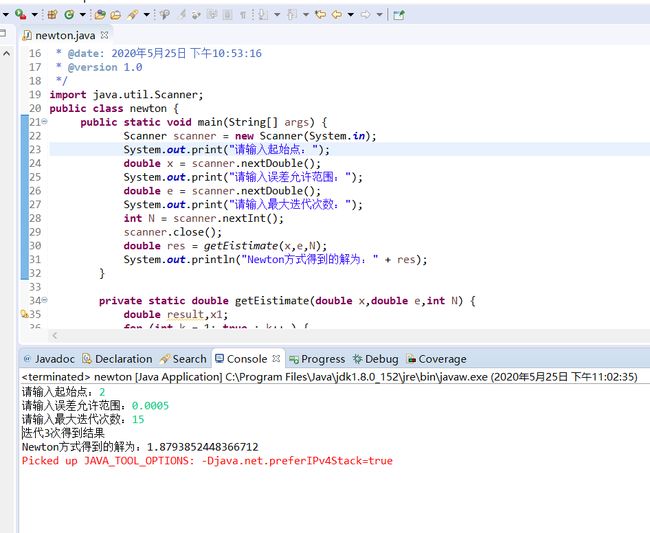
(1)牛顿法:
/**
* @Title: newton.java
* @Desc: TODO
* @Package: root
* @author: glm233
* @date: 2020年5月25日 下午10:53:16
* @version 1.0
*/
package root;
/**
* @ClassName: newton
* @Desc: TODO
* @author: glm233
* @date: 2020年5月25日 下午10:53:16
* @version 1.0
*/
import java.util.Scanner;
public class newton {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
System.out.print("请输入起始点:");
double x = scanner.nextDouble();
System.out.print("请输入误差允许范围:");
double e = scanner.nextDouble();
System.out.print("请输入最大迭代次数:");
int N = scanner.nextInt();
scanner.close();
double res = getEistimate(x,e,N);
System.out.println("牛顿法得到的解为:" + res);
}
private static double getEistimate(double x,double e,int N) {
double result,x1;
for (int k = 1; true ; k++ ) {
if(f(x) == 0){
throw new RuntimeException("出现奇异情况....");
}
x1 = x - F(x)/f(x);
if(Math.abs(x1 - x) < e ){
System.out.println("迭代" + k + "次得到结果");
return x1;
}
if(k == N){
throw new RuntimeException("迭代失败,已达最大迭代次数N....");
}
x = x1;
}
}
private static double F(double x) {
return x*x*x -3*x-1;
}
private static double f(double x) {
return 3*x*x -3;
}
}
运行结果:
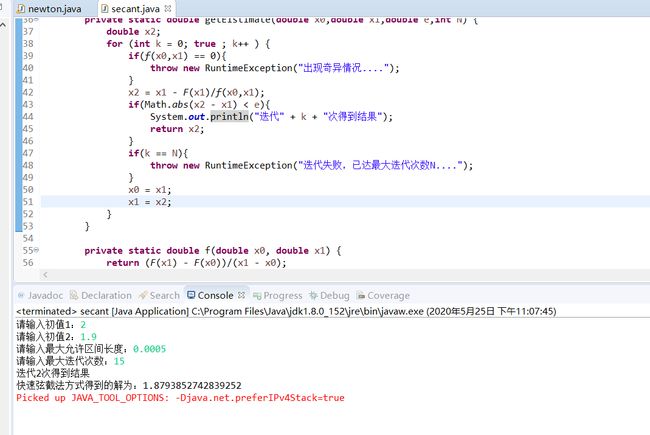
(2)用弦截法,取 x 0 = 2 , x 1 = 1.9 x_0=2,x_1=1.9 x0=2,x1=1.9
/**
* @Title: secant.java
* @Desc: TODO
* @Package: root
* @author: glm233
* @date: 2020年5月25日 下午11:05:56
* @version 1.0
*/
package root;
import java.util.Scanner;
/**
* @ClassName: secant
* @Desc: TODO
* @author: glm233
* @date: 2020年5月25日 下午11:05:56
* @version 1.0
*/
public class secant {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
System.out.print("请输入初值1:");
double x0 = scanner.nextDouble();
System.out.print("请输入初值2:");
double x1 = scanner.nextDouble();
System.out.print("请输入误差允许范围:");
double e = scanner.nextDouble();
System.out.print("请输入最大迭代次数:");
int N = scanner.nextInt();
scanner.close();
double res = getEistimate(x0,x1,e,N);
System.out.println("快速弦截法得到的解为:" + res);
}
private static double getEistimate(double x0,double x1,double e,int N) {
double x2;
for (int k = 0; true ; k++ ) {
if(f(x0,x1) == 0){
throw new RuntimeException("出现奇异情况....");
}
x2 = x1 - F(x1)/f(x0,x1);
if(Math.abs(x2 - x1) < e){
System.out.println("迭代" + k + "次得到结果");
return x2;
}
if(k == N){
throw new RuntimeException("迭代失败,已达最大迭代次数N....");
}
x0 = x1;
x1 = x2;
}
}
private static double f(double x0, double x1) {
return (F(x1) - F(x0))/(x1 - x0);
}
private static double F(double x) {
return x*x*x -3*x-1;
}
}
运行结果:
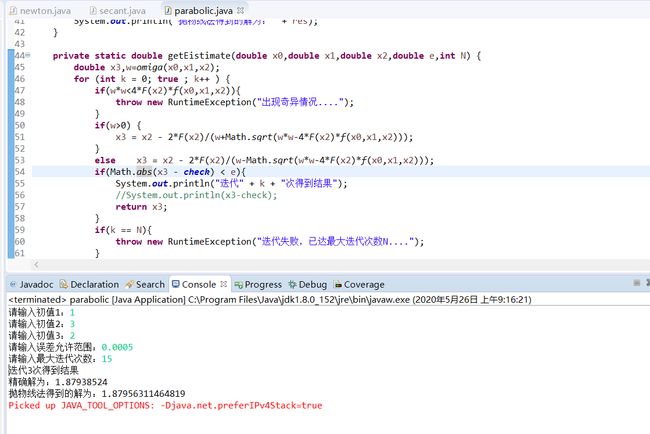
(3)用抛物线法,取 x 0 = 1 , x 1 = 3 , x 2 = 2 x_0=1,x_1=3,x_2=2 x0=1,x1=3,x2=2
/**
* @Title: parabolic.java
* @Desc: TODO
* @Package: root
* @author: glm233
* @date: 2020年5月25日 下午11:10:01
* @version 1.0
*/
package root;
import java.util.Scanner;
/**
* @ClassName: parabolic
* @Desc: TODO
* @author: glm233
* @date: 2020年5月25日 下午11:10:01
* @version 1.0
*/
public class parabolic {
public final static double check=1.87938524;
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
System.out.print("请输入初值1:");
double x0 = scanner.nextDouble();
System.out.print("请输入初值2:");
double x1 = scanner.nextDouble();
System.out.print("请输入初值3:");
double x2 = scanner.nextDouble();
System.out.print("请输入误差允许范围:");
double e = scanner.nextDouble();
System.out.print("请输入最大迭代次数:");
int N = scanner.nextInt();
scanner.close();
double res = getEistimate(x0,x1,x2,e,N);
System.out.println("精确解为:" + check);
System.out.println("抛物线法得到的解为:" + res);
}
private static double getEistimate(double x0,double x1,double x2,double e,int N) {
double x3,w=omiga(x0,x1,x2);
for (int k = 0; true ; k++ ) {
if(w*w<4*F(x2)*f(x0,x1,x2)){
throw new RuntimeException("出现奇异情况....");
}
if(w>0) {
x3 = x2 - 2*F(x2)/(w+Math.sqrt(w*w-4*F(x2)*f(x0,x1,x2)));
}
else x3 = x2 - 2*F(x2)/(w-Math.sqrt(w*w-4*F(x2)*f(x0,x1,x2)));
if(Math.abs(x3 - check) < e){
System.out.println("迭代" + k + "次得到结果");
//System.out.println(x3-check);
return x2;
}
if(k == N){
throw new RuntimeException("迭代失败,已达最大迭代次数N....");
}
//System.out.println(x3);
x0 = x1;
x1 = x2;
x2 = x3;
}
}
private static double omiga(double x0,double x1,double x2){
return f(x0,x1,x2)*(x2-x1)+f(x2,x1);
}
private static double f(double x0, double x1) {
return (F(x1) - F(x0))/(x1 - x0);
}
private static double f(double x0, double x1,double x2) {
return (f(x1,x2)-f(x1,x0))/(x2-x0);
}
private static double F(double x) {
return x*x*x -3*x-1;
}
}
运行结果: