#2019-2020 ICPC, NERC, Southern and Volga Russian Regional Contest 部分题解

A. Berstagram

time limit per test

3 seconds

memory limit per test

512 megabytes

input

standard input

output

standard output

Polycarp recently signed up to a new social network Berstagram. He immediately published nn posts there. He assigned numbers from 11 to nn to all posts and published them one by one. So, just after publishing Polycarp's news feed contained posts from 11 to nn — the highest post had number 11, the next one had number 22, ..., the lowest post had number nn.

After that he wrote down all likes from his friends. Likes were coming consecutively from the 11-st one till the mm-th one. You are given a sequence a1,a2,…,ama1,a2,…,am (1≤aj≤n1≤aj≤n), where ajaj is the post that received the jj-th like.

News feed in Berstagram works in the following manner. Let's assume the jj-th like was given to post ajaj. If this post is not the highest (first) one then it changes its position with the one above. If ajaj is the highest post nothing changes.

For example, if n=3n=3, m=5m=5 and a=[3,2,1,3,3]a=[3,2,1,3,3], then Polycarp's news feed had the following states:

• before the first like: [1,2,3][1,2,3];
• after the first like: [1,3,2][1,3,2];
• after the second like: [1,2,3][1,2,3];
• after the third like: [1,2,3][1,2,3];
• after the fourth like: [1,3,2][1,3,2];
• after the fifth like: [3,1,2][3,1,2].

Polycarp wants to know the highest (minimum) and the lowest (maximum) positions for each post. Polycarp considers all moments of time, including the moment "before all likes".

Input

The first line contains two integer numbers nn and mm (1≤n≤1051≤n≤105, 1≤m≤4⋅1051≤m≤4⋅105) — number of posts and number of likes.

The second line contains integers a1,a2,…,ama1,a2,…,am (1≤aj≤n1≤aj≤n), where ajaj is the post that received the jj-th like.

Output

Print nn pairs of integer numbers. The ii-th line should contain the highest (minimum) and the lowest (maximum) positions of the ii-th post. You should take into account positions at all moments of time: before all likes, after each like and after all likes. Positions are numbered from 11 (highest) to nn (lowest).

Examples

input

Copy

3 5
3 2 1 3 3

output

Copy

1 2
2 3
1 3

input

Copy

10 6
7 3 5 7 3 6

output

Copy

1 2
2 3
1 3
4 7
4 5
6 7
5 7
8 8
9 9
10 10

题目大意 ： 有一个长度为N包含1到N的序列， M次操作， 每次将数 X 与他前面的数进行交换，如果该数已经是第一个数，则忽略本次操作，最后输出每个点在这些过程中出现的下标最小的位置和下标最大的位置

思路 ：签到题，直接数组模拟就好

Accepted code 

#include
#include
using namespace std;

#define sc scanf
#define ls rt << 1
#define rs ls | 1
#define Min(x, y) x = min(x, y)
#define Max(x, y) x = max(x, y)
#define ALL(x) (x).begin(),(x).end()
#define SZ(x) ((int)(x).size())
#define MEM(x, b) memset(x, b, sizeof(x))
#define lowbit(x) ((x) & -(x))
#define P2(x) ((x) * (x))

typedef long long ll;
const int MOD = 1e9 + 7;
const int MAXN = 1e6 + 100;
const int INF = 0x3f3f3f3f;
inline ll fpow(ll a, ll b){ ll r = 1, t = a; while (b){ if (b & 1)r = (r*t) % MOD; b >>= 1; t = (t*t) % MOD; }return r; }

int p[MAXN], n, m;
int max_[MAXN], min_[MAXN];
unordered_map  mp;

int main()
{
	cin >> n >> m;
	for (int i = 1; i <= n; i++) max_[i] = min_[i] = p[i] = i, mp[i] = i;
	for (int i = 1; i <= m; i++) {
		int tmp; sc("%d", &tmp);
		if (p[1] == tmp) continue; // 第一个位置忽略
		int xi = mp[tmp]; 
		swap(p[xi], p[xi - 1]);  // 交换
		mp[tmp] = xi - 1, mp[p[xi]] = xi; 
		Min(min_[tmp], xi - 1); Max(max_[p[xi]], xi);
	}
	for (int i = 1; i <= n; i++) cout << min_[i] << " " << max_[i] << endl;
	return 0;
}

B. The Feast and the Bus

time limit per test

2 seconds

memory limit per test

512 megabytes

input

standard input

output

standard output

Employees of JebTrains are on their way to celebrate the 256-th day of the year! There are nn employees and kk teams in JebTrains. Each employee is a member of some (exactly one) team. All teams are numbered from 11 to kk. You are given an array of numbers t1,t2,…,tnt1,t2,…,tn where titi is the ii-th employee's team number.

JebTrains is going to rent a single bus to get employees to the feast. The bus will take one or more rides. A bus can pick up an entire team or two entire teams. If three or more teams take a ride together they may start a new project which is considered unacceptable. It's prohibited to split a team, so all members of a team should take the same ride.

It is possible to rent a bus of any capacity ss. Such a bus can take up to ss people on a single ride. The total cost of the rent is equal to s⋅rs⋅r burles where rr is the number of rides. Note that it's impossible to rent two or more buses.

Help JebTrains to calculate the minimum cost of the rent, required to get all employees to the feast, fulfilling all the conditions above.

Input

The first line contains two integers nn and kk (1≤n≤5⋅105,1≤k≤80001≤n≤5⋅105,1≤k≤8000) — the number of employees and the number of teams in JebTrains. The second line contains a sequence of integers t1,t2,…,tnt1,t2,…,tn, where titi (1≤ti≤k1≤ti≤k) is the ii-th employee's team number. Every team contains at least one employee.

Output

Print the minimum cost of the rent.

Examples

input

Copy

6 3
3 1 2 3 2 3

output

Copy

6

input

Copy

10 1
1 1 1 1 1 1 1 1 1 1

output

Copy

10

input

Copy

12 4
1 2 3 1 2 3 4 1 2 1 2 1

output

Copy

12

题目大意 ：有N个学生， 他们属于1到K组（每组至少有一个学生）， 有若干辆公交车，公交车一次可以载1到2组学生， 输出一个最小值 ：公交车的数量 * 所有公交车中所载的学生数量最大值

思路 ：贪心 + 枚举的思想， 先对每组学生数量进行排序，易知公交车的数量一定在N / 2到 K之间（对于偶数N是N / 2， 奇数是N / 2 + 1），所以直接枚举公交车的数量，最开始类似高斯求1 到 100的和那样组队匹配， 然后每多一组就将当前人数最多的一组分到单独一组， 每次记录最小值即可

Accepted code

#include
#include
using namespace std;

#define sc scanf
#define ls rt << 1
#define rs ls | 1
#define Min(x, y) x = min(x, y)
#define Max(x, y) x = max(x, y)
#define ALL(x) (x).begin(),(x).end()
#define SZ(x) ((int)(x).size())
#define MEM(x, b) memset(x, b, sizeof(x))
#define lowbit(x) ((x) & -(x))
#define P2(x) ((x) * (x))

typedef long long ll;
const int MOD = 1e9 + 7;
const int MAXN = 1e6 + 100;
const ll INF = 0x3f3f3f3f3f3f3f3f;
inline ll fpow(ll a, ll b){ ll r = 1, t = a; while (b){ if (b & 1)r = (r*t) % MOD; b >>= 1; t = (t*t) % MOD; }return r; }

ll p[MAXN], n, k, sum, ans = INF;

int main()
{
	cin >> n >> k;
	for (ll i = 1; i <= n; i++) {
		ll tmp; sc("%lld", &tmp);
		p[tmp]++;  // 每组的人数
	}
	sort(p + 1, p + k + 1); Min(ans, k * p[k]); // 分K组
	for (ll i = k; i > 1; i--) {
		ll tmp = i / 2 + k - i, max_ = -1;  // 枚举公交车数量 
		if (i & 1) tmp++;
		if (i != k) Max(max_, p[k]);
		for (ll j = 1; j <= i / 2; j++) {
			Max(max_, p[j] + p[i - j + 1]);
		}
		Min(ans, max_ * tmp);
	}
	cout << ans << endl;
	return 0;
}

C. Trip to Saint Petersburg

time limit per test

3 seconds

memory limit per test

512 megabytes

input

standard input

output

standard output

You are planning your trip to Saint Petersburg. After doing some calculations, you estimated that you will have to spend kk rubles each day you stay in Saint Petersburg — you have to rent a flat, to eat at some local cafe, et cetera. So, if the day of your arrival is LL, and the day of your departure is RR, you will have to spend k(R−L+1)k(R−L+1) rubles in Saint Petersburg.

You don't want to spend a lot of money on your trip, so you decided to work in Saint Petersburg during your trip. There are nn available projects numbered from 11 to nn, the ii-th of them lasts from the day lili to the day riri inclusive. If you choose to participate in the ii-th project, then you have to stay and work in Saint Petersburg for the entire time this project lasts, but you get paid pipi rubles for completing it.

Now you want to come up with an optimal trip plan: you have to choose the day of arrival LL, the day of departure RR and the set of projects SS to participate in so that all the following conditions are met:

• your trip lasts at least one day (formally, R≥LR≥L);
• you stay in Saint Petersburg for the duration of every project you have chosen (formally, for each s∈Ss∈S L≤lsL≤ls and R≥rsR≥rs);
• your total profit is strictly positive and maximum possible (formally, you have to maximize the value of ∑s∈Sps−k(R−L+1)∑s∈Sps−k(R−L+1), and this value should be positive).

You may assume that no matter how many projects you choose, you will still have time and ability to participate in all of them, even if they overlap.

Input

The first line contains two integers nn and kk (1≤n≤2⋅1051≤n≤2⋅105, 1≤k≤10121≤k≤1012) — the number of projects and the amount of money you have to spend during each day in Saint Petersburg, respectively.

Then nn lines follow, each containing three integers lili, riri, pipi (1≤li≤ri≤2⋅1051≤li≤ri≤2⋅105, 1≤pi≤10121≤pi≤1012) — the starting day of the ii-th project, the ending day of the ii-th project, and the amount of money you get paid if you choose to participate in it, respectively.

Output

If it is impossible to plan a trip with strictly positive profit, print the only integer 00.

Otherwise, print two lines. The first line should contain four integers pp, LL, RR and mm — the maximum profit you can get, the starting day of your trip, the ending day of your trip and the number of projects you choose to complete, respectively. The second line should contain mm distinct integers s1s1, s2s2, ..., smsm — the projects you choose to complete, listed in arbitrary order. If there are multiple answers with maximum profit, print any of them.

Examples

input

Copy

4 5
1 1 3
3 3 11
5 5 17
7 7 4

output

Copy

13 3 5 2
3 2 

input

Copy

1 3
1 2 5

output

Copy

0

input

Copy

4 8
1 5 16
2 4 9
3 3 24
1 5 13

output

Copy

22 1 5 4
3 2 1 4 

题目大意 ：你在城市找工作，有N个工作，每个工作如果从L工作到R（中间不间断）会得到W的赏金，但是只要你在这个城市一天，你就会失去K元， 现在让你输出你的最大盈利，并输出你从第几天到第几天留在这个城市和参加的工作的编号， 如果你无论如何都无法盈利， 输出0

思路 ：区间线段问题，要输出的是盈利的最大值， 也很容易就往线段树维护区间最大值上靠：首先将所有的线段加入线段树，包括每天的亏损，然后对工作的区间按L从小到大排个序，枚举左端点， 如果当前左端点会使某个工作无法开展， 那么将左端点往前全部清空， 并记录最大值， 枚举完之后， 就可以直到最大的盈利和左端点了， 但是现在还得找到右端点， 可以将整颗线段树全部清空， 将找到的左端点靠右的加入线段树， 并依次按照右端点从左往右加入，直到某次的答案等于记录的最大值， 退出， 最后输出

Accepted code

#include
#include
using namespace std;

#define sc scanf
#define ls rt << 1
#define rs ls | 1
#define Min(x, y) x = min(x, y)
#define Max(x, y) x = max(x, y)
#define ALL(x) (x).begin(),(x).end()
#define SZ(x) ((int)(x).size())
#define MEM(x, b) memset(x, b, sizeof(x))
#define lowbit(x) ((x) & -(x))
#define P2(x) ((x) * (x))

typedef long long ll;
const int MOD = 1e9 + 7;
const int MAXN = 2e5 + 100;
const ll INF = 0x3f3f3f3f3f3f3f3f;
inline ll fpow(ll a, ll b){ ll r = 1, t = a; while (b){ if (b & 1)r = (r*t) % MOD; b >>= 1; t = (t*t) % MOD; }return r; }

struct node
{
	ll id, x, y, w;
	bool operator < (const node &oth) const
	{
		return x < oth.x;
	}
}p[MAXN];
bool cmp(node a, node b) {
	return a.y < b.y;
}
struct Tree
{
	ll l, r, ans, lzy;
}t[MAXN * 4];
ll n, m, k, tot = 1, now = 1, max_ = -INF, N;
ll pre[MAXN], L, R, X;
void Build(ll rt, ll l, ll r) {
	t[rt].l = l, t[rt].r = r;
	t[rt].ans = t[rt].lzy = 0;
	if (l == r) return;
	ll mid = (l + r) >> 1;
	Build(ls, l, mid);
	Build(rs, mid + 1, r);
}
void Pushdown(ll rt) {
	t[ls].lzy += t[rt].lzy, t[rs].lzy += t[rt].lzy;
	t[ls].ans += t[rt].lzy, t[rs].ans += t[rt].lzy;
	t[rt].lzy = 0;
}
void Update(ll rt, ll l, ll r, ll pos) {
	if (t[rt].l >= l && t[rt].r <= r) {
		t[rt].ans += pos; t[rt].lzy += pos;
		return;
	}
	ll mid = (t[rt].l + t[rt].r) >> 1;
	if (t[rt].lzy) Pushdown(rt);
	if (mid < l) Update(rs, l, r, pos);
	else if (mid >= r) Update(ls, l, r, pos);
	else {
		Update(ls, l, mid, pos);
		Update(rs, mid + 1, r, pos);
	}
	t[rt].ans = max(t[ls].ans, t[rs].ans);
}

int main()
{
	cin >> n >> k;
	for (ll i = 1; i <= n; i++) {
		sc("%lld %lld %lld", &p[i].x, &p[i].y, &p[i].w);
		p[i].id = i;
		Max(N, p[i].y);
	}
	Build(1, 1, N); sort(p + 1, p + n + 1);  // 左端点排序
	for (ll i = 1; i <= N; i++) Update(1, i, N, -k);
	for (ll i = 1; i <= n; i++) Update(1, p[i].y, N, p[i].w);  
	for (ll i = 1; i <= N; i++) {
		while (i > p[now].x && now <= n) {
			Update(1, p[now].y, N, -p[now].w);  // 枚举L
			now++;
		}
		if (max_ < t[1].ans) { max_ = t[1].ans, L = i; }
		Update(1, i, N, k);
	}
	if (max_ <= 0) { printf("0\n"); return 0; }  // 已知答案
	Build(1, 1, N);
	for (ll i = L; i <= N; i++) Update(1, i, N, -k);  // 清空
	sort(p + 1, p + n + 1, cmp);  // 按R排序
	for (ll i = 1; i <= n; i++) {
		if (p[i].x >= L) { Update(1, p[i].y, N, p[i].w); R = p[i].y; } //更新
		if (t[1].ans == max_) break;
	}
	for (ll i = 1; i <= n; i++) 
		if (p[i].x >= L && p[i].y <= R) pre[++X] = p[i].id;
	printf("%lld %lld %lld %lld\n", max_, L, R, X);
	for (ll i = 1; i <= X; i++) printf("%lld ", pre[i]);
	printf("\n");
	return 0;  // 改数组大小!!!
}

F. Data Center

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

You are developing a project to build a new data center. The data center will be a rectangle with an area of exactly nn square meters. Each side of the data center must be an integer.

Your goal is to minimize the impact of the external environment on the data center. For this reason, you want to minimize the length of the perimeter of the data center (that is, the sum of the lengths of its four sides).

What is the minimum perimeter of a rectangular data center with an area of exactly nn square meters, if the lengths of all its sides must be integers?

Input

The first and only line of the input contains an integer nn (1≤n≤1051≤n≤105), where nn is the area of the data center in square meters.

Output

Print the required minimum perimeter in meters.

Examples

input

Copy

36

output

Copy

24

input

Copy

13

output

Copy

28

input

Copy

1

output

Copy

4

Note

In the first example, the required shape of the data center is 6×66×6 square. Its area is 3636 and the perimeter is 6+6+6+6=246+6+6+6=24.

In the second example, the required shape of the data center is 1×131×13 rectangle. Its area is 1313 and the perimeter is 1+13+1+13=281+13+1+13=28.

In the third example, the required shape of the data center is 1×11×1 square. Its area is 11 and the perimeter is 1+1+1+1=41+1+1+1=4.

题目大意 ：输入一个矩形的面积， 输出最小周长

思路 ：签到题，枚举所有的因子即可

Accepted code

#include
#include
using namespace std;

#define sc scanf
#define ls rt << 1
#define rs ls | 1
#define Min(x, y) x = min(x, y)
#define Max(x, y) x = max(x, y)
#define ALL(x) (x).begin(),(x).end()
#define SZ(x) ((int)(x).size())
#define MEM(x, b) memset(x, b, sizeof(x))
#define lowbit(x) ((x) & -(x))
#define P2(x) ((x) * (x))

typedef long long ll;
const int MOD = 1e9 + 7;
const int MAXN = 2e5 + 100;
const int INF = 0x3f3f3f3f;
inline ll fpow(ll a, ll b){ ll r = 1, t = a; while (b){ if (b & 1)r = (r*t) % MOD; b >>= 1; t = (t*t) % MOD; }return r; }

int main()
{
	int n; cin >> n;
	int max_ = INF;
	for (int i = 1; i <= sqrt(n); i++) {
		if (n % i != 0) continue;
		int ai = i, bi = n / i;
		Min(max_, 2 * ai + 2 * bi);
	}
	cout << max_ << endl;
	return 0;
}

H. Happy Birthday

time limit per test

2 seconds

memory limit per test

512 megabytes

input

standard input

output

standard output

You have a set of birthday cake candles. Each of such candles represents a digit between 00 and 99, inclusive.

Example of birthday cake candles.

Let's denote the candle representing the digit dd as dd-candle.

Your set contains c0c0 instances of 00-candles, c1c1 instances of 11-candles and so on. So, the total number of candles is c0+c1+⋯+c9c0+c1+⋯+c9.

These digits are needed to wish your cat a happy birthday. For each birthday, starting with the first, you want to compose the age of the cat using the digits from the set.

Since you light candles for a very short time, candles don't have time to burn out. For this reason you can reuse candles an arbitrary number of times (therefore your set of candles never changes).

For example, if you have one instance of each digit (i.e. c0=c1=⋯=c9=1c0=c1=⋯=c9=1), you can compose any number from 11 to 1010 using this set, but you cannot compose 1111.

You have to determine the first birthday, on which you cannot compose the age of the cat using the candles from your set. In other words, find the minimum number yy such that all numbers from 11 to y−1y−1 can be composed by digits from your set, but yy cannot be composed.

Input

The first line contains an integer tt (1≤t≤1041≤t≤104) — the number of test cases in the input.

The only line of each test case contains ten integer numbers c0,c1,…,c9c0,c1,…,c9 (0≤ci≤1050≤ci≤105) — the number of 00-candles, 11-candles, 22-candles and so on.

It is guaranteed that the sum of all cici in the input does not exceed 106106.

Output

For each test case, output one integer in single line — the minimum age which cannot be composed by candles from your set. Please note that the age can be quite large (it may exceed the standard 64-bit integer types in your programming language).

Example

input

Copy

4
1 1 1 1 1 1 1 1 1 1
0 0 1 1 2 2 3 3 4 4
1 2 1 2 1 3 1 0 0 0
0 1 2 1 4 3 1 1 2 1

output

Copy

11
1
7
10

题目大意 ：有输入0 到 9蜡烛的数量， 输出这些蜡烛不能组成的最小数（组成即两个蜡烛拼在一起， 且该数字必须大于0） 

思路 ：数字很大， 可以找规律来写， 分以下情况，首先是他们的数量都一样，那么答案就是1的总数组成的字符串。如果有不一样的，看最小的是否是0， 如果是， 0不能当前导，所以答案就是1后面跟num【0】 + 1个0 ，如果不是0，那么输出num【x】 + 1次。如果最小次数不是0，直接输出num【x】 + 1次该数

Accepted code

#include
#include
using namespace std;

#define sc scanf
#define ls rt << 1
#define rs ls | 1
#define Min(x, y) x = min(x, y)
#define Max(x, y) x = max(x, y)
#define ALL(x) (x).begin(),(x).end()
#define SZ(x) ((int)(x).size())
#define MEM(x, b) memset(x, b, sizeof(x))
#define lowbit(x) ((x) & -(x))
#define P2(x) ((x) * (x))

typedef long long ll;
const int MOD = 1e9 + 7;
const int MAXN = 2e5 + 100;
const int INF = 0x3f3f3f3f;
inline ll fpow(ll a, ll b){ ll r = 1, t = a; while (b){ if (b & 1)r = (r*t) % MOD; b >>= 1; t = (t*t) % MOD; }return r; }

int p[15];
set  st;
int min_, id, flag;
void init() {
	st.clear(); min_ = id = INF;
	flag = -1;
}

int main()
{
	int T; cin >> T;
	while (T--) {
		init();
		for (int i = 0; i < 10; i++) {
			int tmp; sc("%d", &tmp); st.insert(tmp);
			if (tmp < min_) { min_ = tmp; id = i; }
			p[i] = tmp;
		}
		if (SZ(st) == 1) {
			for (auto it : st) {
				for (int i = 0; i <= it; i++) cout << "1";
			}
			cout << endl; continue;
		}
		if (id == 0) {
			int tmp = -1;
			for (int i = 1; i < 10; i++) {
				if (p[i] == min_) { tmp = i; break; }
			}
			if (tmp != -1) {
				for (int i = 0; i <= min_; i++) cout << tmp;
				cout << endl;
			}
			else {
				cout << "1";
				for (int i = 0; i <= min_; i++) cout << "0";
				cout << endl;
			}
		}
		else {
			for (int i = 0; i <= min_; i++) cout << id;
			cout << endl;
		}
	}
	return 0;
}

J. The Parade

time limit per test

2 seconds

memory limit per test

512 megabytes

input

standard input

output

standard output

The Berland Army is preparing for a large military parade. It is already decided that the soldiers participating in it will be divided into kk rows, and all rows will contain the same number of soldiers.

Of course, not every arrangement of soldiers into kk rows is suitable. Heights of all soldiers in the same row should not differ by more than 11. The height of each soldier is an integer between 11 and nn.

For each possible height, you know the number of soldiers having this height. To conduct a parade, you have to choose the soldiers participating in it, and then arrange all of the chosen soldiers into kk rows so that both of the following conditions are met:

• each row has the same number of soldiers,
• no row contains a pair of soldiers such that their heights differ by 22 or more.

Calculate the maximum number of soldiers who can participate in the parade.

Input

The first line contains one integer tt (1≤t≤100001≤t≤10000) — the number of test cases. Then the test cases follow.

Each test case begins with a line containing two integers nn and kk (1≤n≤300001≤n≤30000, 1≤k≤10121≤k≤1012) — the number of different heights of soldiers and the number of rows of soldiers in the parade, respectively.

The second (and final) line of each test case contains nn integers c1c1, c2c2, ..., cncn (0≤ci≤10120≤ci≤1012), where cici is the number of soldiers having height ii in the Berland Army.

It is guaranteed that the sum of nn over all test cases does not exceed 3000030000.

Output

For each test case, print one integer — the maximum number of soldiers that can participate in the parade.

Example

input

Copy

5
3 4
7 1 13
1 1
100
1 3
100
2 1
1000000000000 1000000000000
4 1
10 2 11 1

output

Copy

16
100
99
2000000000000
13

Note

Explanations for the example test cases:

1. the heights of soldiers in the rows can be: [3,3,3,3][3,3,3,3], [1,2,1,1][1,2,1,1], [1,1,1,1][1,1,1,1], [3,3,3,3][3,3,3,3] (each list represents a row);
2. all soldiers can march in the same row;
3. 3333 soldiers with height 11 in each of 33 rows;
4. all soldiers can march in the same row;
5. all soldiers with height 22 and 33 can march in the same row.

题目大意 ： 1到N身高为 i 的人数为x【i】， 现在让你把所有人分成不超过K行， 保证每一行的人数相等且一行的两个人的身高差距不超过1， 输出这个队伍最多可以安排多少人

思路 ： 不难想到要二分答案， 二分每一行站多少人， 然后从第一行开始判断， 如果该方案成立， 答案往大的走， 否则往小的走， 如果没有方案， 输出0

Accepted code

#include
#include
using namespace std;

#define sc scanf
#define ls rt << 1
#define rs ls | 1
#define Min(x, y) x = min(x, y)
#define Max(x, y) x = max(x, y)
#define ALL(x) (x).begin(),(x).end()
#define SZ(x) ((int)(x).size())
#define MEM(x, b) memset(x, b, sizeof(x))
#define lowbit(x) ((x) & -(x))
#define P2(x) ((x) * (x))

typedef long long ll;
const int MOD = 1e9 + 7;
const int MAXN = 1e5 + 100;
const int INF = 0x3f3f3f3f;
inline ll fpow(ll a, ll b){ ll r = 1, t = a; while (b){ if (b & 1)r = (r*t) % MOD; b >>= 1; t = (t*t) % MOD; }return r; }

ll p[MAXN], k, mid;
int n;
bool flag;
void dfs(ll last, ll now, ll step) { // last表示上次剩下的，ans表示当前的，step表示行数
	if (!flag) return;
	if (step >= k || now > n) {
		if (step < k) flag = false;
		return;
	}
	ll ans = p[now]; ans += last; bool s = false;
	if (ans < mid && step == k) { flag = false; return; }
	if (ans < mid) dfs(ans - last, now + 1, step);  // 当前行没有放，减去上一次的
	else {
		ll cnt = min(ans / mid, k - step);
		ll tot = ans - cnt * mid;
		dfs(tot, now + 1, step + cnt);
	}
}

int main()
{
	int T; cin >> T;
	while (T--) {
		sc("%d %lld", &n, &k); ll sum = 0;
		for (int i = 1; i <= n; i++) {
			sc("%lld", &p[i]);
			if (i > 1) Max(sum, p[i - 1] + p[i]); 
		}
		if (n == 1) sum = p[1];
		ll l = 1, r = sum, max_ = 0;
		while (l <= r) {
			mid = (l + r) >> 1; flag = true;
			dfs(0, 1, 0);
			if (flag) Max(max_, mid * k), l = mid + 1;
			else r = mid - 1;
		}
		printf("%lld\n", max_);
	}
	return 0;
}

L. Divide The Students

time limit per test

2 seconds

memory limit per test

512 megabytes

input

standard input

output

standard output

A group of students has recently been admitted to the Faculty of Computer Sciences at the Berland State University. Now the programming teacher wants to divide them into three subgroups for practice sessions.

The teacher knows that a lot of programmers argue which language is the best. The teacher doesn't want to hear any arguments in the subgroups, so she wants to divide the students into three subgroups so that no pair of students belonging to the same subgroup want to argue.

To perform this division, the teacher asked each student which programming language he likes. There are aa students who answered that they enjoy Assembler, bb students stated that their favourite language is Basic, and cc remaining students claimed that C++ is the best programming language — and there was a large argument between Assembler fans and C++ fans.

Now, knowing that Assembler programmers and C++ programmers can start an argument every minute, the teacher wants to divide the students into three subgroups so that every student belongs to exactly one subgroup, and there is no subgroup that contains at least one Assembler fan and at least one C++ fan. Since teaching a lot of students can be difficult, the teacher wants the size of the largest subgroup to be minimum possible.

Please help the teacher to calculate the minimum possible size of the largest subgroup!

Input

The first line contains one integer tt (1≤t≤51≤t≤5) — the number of test cases in the input. Then test cases follow.

Each test case consists of one line containing three integers aa, bb and cc (1≤a,b,c≤10001≤a,b,c≤1000) — the number of Assembler fans, Basic fans and C++ fans, respectively.

Output

For each test case print one integer — the minimum size of the largest subgroup if the students are divided in such a way that there is no subgroup that contains at least one Assembler fan and at least one C++ fan simultaneously.

Examples

input

Copy

5
3 5 7
4 8 4
13 10 13
1000 1000 1000
13 22 7

output

Copy

5
6
13
1000
14

input

Copy

5
1 3 4
1000 1000 1
4 1 2
325 226 999
939 861 505

output

Copy

3
667
3
517
769

Note

Explanation of the answers for the example 11:

1. The first subgroup contains 33 Assembler fans and 22 Basic fans, the second subgroup — 55 C++ fans, the third subgroup — 22 C++ fans and 33 Basic fans.
2. The first subgroup contains 44 Assembler fans, the second subgroup — 66 Basic fans, the third subgroup — 22 Basic fans and 44 C++ fans.
3. The first subgroup contains all Assembler fans, the second subgroup — all Basic fans, the third subgroup — all C++ fans.
4. The first subgroup contains all Assembler fans, the second subgroup — all Basic fans, the third subgroup — all C++ fans.
5. The first subgroup contains 1212 Assembler fans and 22 Basic fans, the second subgroup — 11 Assembler fan and 1313 Basic fans, the third subgroup — 77 Basic fans and 77 C++ fans.

题目大意 ：有三组学生 A， B,  C， A与C不能放一组， 现在让你分组， 输出三组中最大人数的最小值

思路 ： 数据比较小， 直接枚举A和C的个数， 然后判就行了， 注意B如果小于A并且B小于C， 出现了B的人分到A组的情况，分的人数不能大于B

Accepted code

#include
#include
using namespace std;

#define sc scanf
#define ls rt << 1
#define rs ls | 1
#define Min(x, y) x = min(x, y)
#define Max(x, y) x = max(x, y)
#define ALL(x) (x).begin(),(x).end()
#define SZ(x) ((int)(x).size())
#define MEM(x, b) memset(x, b, sizeof(x))
#define lowbit(x) ((x) & -(x))
#define P2(x) ((x) * (x))

typedef long long ll;
const int MOD = 1e9 + 7;
const int MAXN = 2e5 + 100;
const int INF = 0x3f3f3f3f;
inline ll fpow(ll a, ll b){ ll r = 1, t = a; while (b){ if (b & 1)r = (r*t) % MOD; b >>= 1; t = (t*t) % MOD; }return r; }

int ai, bi, ci, T;

int main()
{
	cin >> T;
	while (T--) {
		sc("%d %d %d", &ai, &bi, &ci);
		int ans = INF; 
		Min(ans, max({ ai, bi, ci }));
		for (int i = 1; i <= 1000; i++) {
			for (int j = 1; j <= 1000; j++) {
				int a = i - ai, c = j - ci;  // a与c的变化值
				int b = bi - a - c;
				if (b > 0 && b <= 1000 && a > -ai && a <= bi && c > -ci && c <= bi && i + j + b == ai + bi + ci) {
					if (bi - b < 0 && abs(a) + abs(c) == abs(bi - b) && a && c) continue;
					Min(ans, max({ i, j, b }));
				}
			}
		}
		cout << ans << endl;
	}
	return 0;
}

N. Wires

time limit per test

3 seconds

memory limit per test

512 megabytes

input

standard input

output

standard output

Polycarpus has a complex electronic device. The core of this device is a circuit board. The board has 109109 contact points which are numbered from 11 to 109109. Also there are nn wires numbered from 11 to nn, each connecting two distinct contact points on the board. An electric signal can pass between wires AA and BB if:

• either both wires share the same contact point;
• or there is a sequence of wires starting with AA and ending with BB, and each pair of adjacent wires in the sequence share a contact point.

The picture shows a circuit board with 55 wires. Contact points with numbers 2,5,7,8,10,132,5,7,8,10,13 are used. Here an electrical signal can pass from wire 22 to wire 33, but not to wire 11.

Currently the circuit board is broken. Polycarpus thinks that the board could be fixed if the wires were re-soldered so that a signal could pass between any pair of wires.

It takes 11 minute for Polycarpus to re-solder an end of a wire. I.e. it takes one minute to change one of the two contact points for a wire. Any contact point from range [1,109][1,109] can be used as a new contact point. A wire's ends must always be soldered to distinct contact points. Both wire's ends can be re-solded, but that will require two actions and will take 22 minutes in total.

Find the minimum amount of time Polycarpus needs to re-solder wires so that a signal can pass between any pair of wires. Also output an optimal sequence of wire re-soldering.

Input

The input contains one or several test cases. The first input line contains a single integer tt — number of test cases. Then, tt test cases follow.

The first line of each test case contains a single integer nn (1≤n≤1051≤n≤105) — the number of wires. The following nn lines describe wires, each line containing two space-separated integers xi,yixi,yi (1≤xi,yi≤1091≤xi,yi≤109, xi≠yixi≠yi) — contact points connected by the ii-th wire. A couple of contact points can be connected with more than one wire.

Sum of values of nn across all test cases does not exceed 105105.

Output

For each test case first print one line with a single integer kk — the minimum number of minutes needed to re-solder wires so that a signal can pass between any pair of wires. In the following kk lines print the description of re-solderings. Each re-soldering should be described by three integers wj,aj,bjwj,aj,bj (1≤wj≤n1≤wj≤n, 1≤aj,bj≤1091≤aj,bj≤109). Such triple means that during the jj-th re-soldering an end of the wjwj-th wire, which was soldered to contact point ajaj, becomes soldered to contact point bjbj instead. After each re-soldering of a wire it must connect two distinct contact points. If there are multiple optimal re-solderings, print any of them.

Example

input

Copy

2
1
4 7
4
1 2
2 3
4 5
5 6

output

Copy

0
1
2 3 5

题目大意 ：输入一个无向图， 要求进行一些操作， 将所有的边放入一个连通块当中，每次可以更改某个边的其中一个顶点， 并输出方案

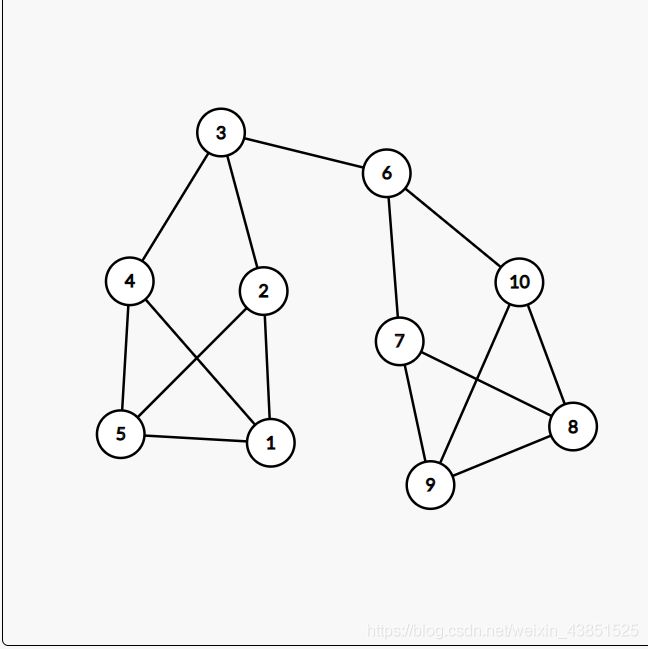
思路 ： 先找一个连通块作为基准，把其他连通块的一条边连到该连通块上就行了，可以通过删除dfs最后一次遍历到的点，一开始我的想法是删除每个连通块的度数最小的点，但是这个想法过不去，如下图：

度数最小为3，答案应该是在点4，2，5，1，7，10，8，9当中删除任意一个对应的边，但是3和6度数也为3，删除后图不连通

 

#include
#include
using namespace std;

#define sc scanf
#define ls rt << 1
#define rs ls | 1
#define Min(x, y) x = min(x, y)
#define Max(x, y) x = max(x, y)
#define ALL(x) (x).begin(),(x).end()
#define SZ(x) ((int)(x).size())
#define MEM(x, b) memset(x, b, sizeof(x))
#define lowbit(x) ((x) & -(x))
#define P2(x) ((x) * (x))

typedef long long ll;
const int MOD = 1e9 + 7;
const int MAXN = 2e5 + 100;
const int INF = 0x3f3f3f3f;
inline ll fpow(ll a, ll b){ ll r = 1, t = a; while (b){ if (b & 1)r = (r*t) % MOD; b >>= 1; t = (t*t) % MOD; }return r; }

struct node
{
	int x, y;
}t[MAXN];
struct Edge
{
	int u, v, id;
};
struct T
{
	int id, u;
}c[MAXN];
vector  e;
vector  edge[MAXN << 1];
int ev[MAXN], m, rt, X;
int tot, cnt, id, C;
bool vis[MAXN];
void init() {
	for (int i = 1; i <= 2 * m; i++) edge[i].clear();
	MEM(vis, 0); tot = X = C = 0;
	e.clear();
}
void dfs(int x, int fa) {
	cnt = x, id = edge[x][0].id;
	vis[x] = true;
	for (int i = 0; i < SZ(edge[x]); i++) {
		int vi = edge[x][i].v;
		if (vi == fa || vis[vi]) continue;
		dfs(vi, x);
	}
}

int main()
{
	int T; cin >> T;
	while (T--) {
		sc("%d", &m); init();
		for (int i = 1; i <= m; i++) {
			sc("%d %d", &t[i].x, &t[i].y);
			e.push_back(t[i].x);
			e.push_back(t[i].y);
		}
		if (m == 1) { printf("0\n"); continue; }
		sort(ALL(e));
		e.erase(unique(ALL(e)), e.end());  // 离散化
		for (int i = 1; i <= m; i++) {
			int xi = t[i].x, yi = t[i].y;
			int ui = lower_bound(ALL(e), xi) - e.begin() + 1;
			int vi = lower_bound(ALL(e), yi) - e.begin() + 1;
			ev[ui] = xi, ev[vi] = yi;
			edge[ui].push_back({ ui, vi, i });  // 存新图
			edge[vi].push_back({ vi, ui, i });
			Max(X, max(ui, vi));  // 找点总数
		}
		bool flag = false;
		for (int i = 1; i <= X; i++) {
			if (!vis[i]) {
				dfs(i, i);
				if (flag) c[++C].u = cnt, c[C].id = id;  // 保存最后一个点
				flag = true;
			}
		}
		if (C == 0) { printf("0\n"); continue; }
		printf("%d\n", C);
		for (int i = 1; i <= C; i++) printf("%d %d %d\n", c[i].id, ev[c[i].u], ev[1]);
	}
	return 0;  // 改数组大小!!!
}