链表、二叉树、图的建立与初始化
注:为了省去输入的麻烦,以下程序所用数据均从文件读取
1、链表建立与初始化
建立如下链表
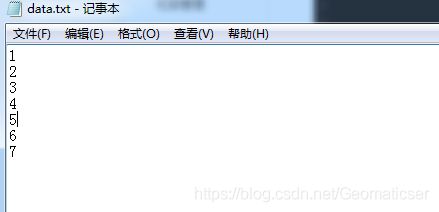
建立一个名为data的txt文件,将此文件放在本程序所在文件夹目录下,文件内容为:
#include
#include
typedef struct LNode
{
int data;
struct LNode *next;
} LNode;
void Print(LNode *L)///输出函数
{
LNode *p;
p=L;
while((p->next)!=NULL)
{
printf("%d ",p->next->data);
p = p->next;
}
}
///建立链表及初始化
LNode *CreatL()
{
LNode *L = (LNode *)malloc(sizeof(LNode)); //申请头结点空间
L->next = NULL; //初始化一个空链表
LNode *r;
r = L; //r始终指向终端结点,开始时指向头结点
int x; //x为链表数据域中的数据
FILE *fp;
fp=fopen("data.txt","r");
while((fscanf(fp,"%d",&x))!=EOF)
{
LNode *p;
p = (LNode *)malloc(sizeof(LNode)); //申请新的结点
p->data = x; //结点数据域赋值
r->next =p;
r = p; //将结点插入到表头L-->|1|-->|2|-->NULL
}
fclose(fp);
r->next=NULL;
return L;
}
void delet(LNode *L,int i)
{
LNode *p=L;
int count=0;
//找到第i个结点的前一个位置p
while(p->next)
{
count++;
if(count==i)
{
break;
}
p=p->next;
}
LNode *q=p->next;
p->next=p->next->next;
free(q);
}
int main()
{
LNode *L;
printf("建立链表:");
L=CreatL();//建立链表与初始化
Print(L);//打印链表
delet(L,3);
printf("\n删除第三个元素后链表:");
Print(L);//打印链表
return 0;
}
/*建立一个名为data的txt文件,将此文件放在本程序所在文件夹目录下
文件内容:
1
2
3
4
5
6
*/
2、二叉树的建立与初始化
下面创建如下图所示二叉树并给出前序遍历调用方法
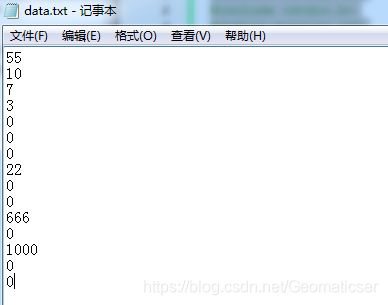
建立一个名为data的txt文件,将此文件放在本程序所在文件夹目录下,文件内容为:
#include
#include
#define maxsize 100
// 定义结点类型
typedef struct btnode
{
int data;
struct btnode *lchild,*rchild;
} btnode;
FILE *fp;///使用文件读取数据
//二叉树
btnode* creat_bitree()
{
int a;
fscanf(fp,"%d",&a);
btnode *node=NULL;
if(a!=0)
{
node=(btnode *)malloc(sizeof(btnode));
node->data=a;
node->lchild =creat_bitree(node->lchild);
node->rchild =creat_bitree(node->rchild);
}
return node;
}
//前序遍历
void pre (btnode *bt)
{
if(bt)
{
printf("%d ",bt->data);
pre(bt->lchild);
pre(bt->rchild);
}
}
int main()
{
fp=fopen("data.txt","r");
btnode *bt=creat_bitree();
printf("\n前序遍历:\n");
pre(bt);
}
/*建立一个名为data的txt文件,将此文件放在本程序所在文件夹目录下
文件内容(按照二叉树前序序列,0表示空指针域):
55
10
7
3
0
0
0
22
0
0
666
0
1000
0
0
*/
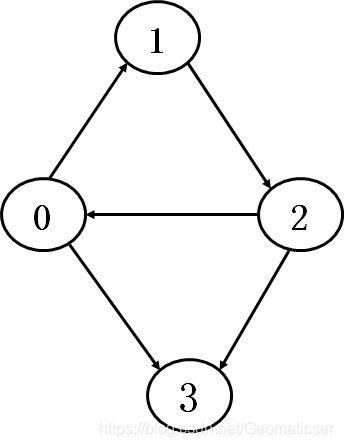
3、有向图图的建立与初始化
建立如下有向图(如何建立无向图代码中有提示)
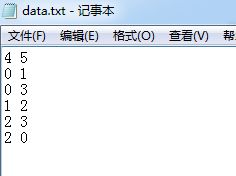
建立一个名为data的txt文件,将此文件放在本程序所在文件夹目录下,文件内容为:
#include
#include
#define DEBUG
#define MAXVEX 100 //最大顶点数
int count=0;
typedef struct ArcNode//边表结点
{
int adjvex;//邻接点域,存储该顶点对应的下标
int weight;//用于存储权值,对于非网图可以不需要
struct ArcNode *nextarc; //链域,指向下一个邻接点
} ArcNode;
typedef struct VNode//顶点表结点
{
int data;//顶点域,存储顶点信息
ArcNode *firstarc;//边表头指针
} VNode;
typedef struct Graph
{
VNode adjList[MAXVEX];
int numNodes, numEdges; // 图中当前顶点数和边数
} Graph;
//图的建立与初始化
Graph *CreateALGraph(Graph *G)
{
G=(Graph *)malloc(sizeof(Graph));
printf("进入:\n");
int i, j, k;
ArcNode *pe;
FILE *fp;
fp=fopen("data.txt","r");
fscanf(fp,"%d %d",&(G->numNodes),&(G->numEdges));
//printf("进入:\n");
printf("顶点数与边数:%d %d\n",G->numNodes,G->numEdges);
for (i = 0 ; i < G->numNodes; i++)
{
G->adjList[i].firstarc = NULL;//将边表置为空表
}
for (k = 0; k < G->numEdges; k++)//建立边表
{
fscanf(fp,"%d %d",&i,&j);
printf("已初始化输入边(%d,%d)\n",i,j);
pe = (ArcNode*)malloc(sizeof(ArcNode));
pe->adjvex = j;//邻接序号为j
//将pe的指针指向当前顶点上指向的结点
pe->nextarc =G->adjList[i].firstarc;
G->adjList[i].firstarc = pe;//将当前顶点的指针指向pe
/*如果是无向图则再添加如下代码
pe = (ArcNode*)malloc(sizeof(ArcNode));
pe->adjvex = i;
pe->nextarc =Gp->adjList[j].firstarc;
Gp->adjList[j].firstarc = pe;
*/
}
return G;
}
//深度优先遍历
void DFS(Graph *G,int v,int visited[])
{
visited[v]=1;
printf("%d ",v);
ArcNode *p=G->adjList[v].firstarc;
while(p)
{
if(visited[p->adjvex]==0)
{
DFS(G,p->adjvex,visited);
}
p=p->nextarc;
}
}
int main()
{
Graph *G;
G=CreateALGraph(G);
int visited[MAXVEX]= {0};
printf("\n深度遍历\n");
DFS(G,1,visited);
return 0;
}
/*所使用文件,第一行为顶点数、边数,之后为对应边
4 5
0 1
0 3
1 2
2 3
2 0
*/