ZJM__
ZJM__

第四周周赛——三金三银两铜+签到

A——HDU 5974    A Simple Math Problem <-题目链接  签到题

Given two positive integers a and b,find suitable X and Y to meet the conditions:
                                                        X+Y=a
                                              Least Common Multiple (X, Y) =b

Input

Input includes multiple sets of test data.Each test data occupies one line,including two positive integers a(1≤a≤2*10^4),b(1≤b≤10^9),and their meanings are shown in the description.Contains most of the 12W test cases.

Output

For each set of input data,output a line of two integers,representing X, Y.If you cannot find such X and Y,output one line of "No Solution"(without quotation).

Sample Input

6 8
798 10780

Sample Output

No Solution
308 490

 

x+y=a

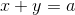
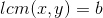
lcm(x,y) = b

这里需要知道一个神奇的结论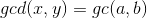：gcd(x,y) = gc(a,b)

和一个普通的结论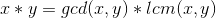：x*y=gcd(x,y)*lcm(x,y)

神奇的结论证明可以：

设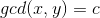gcd(x,y) = c;

x=ci      y=cj

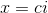
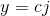
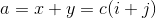
a = x+y=c(i+j)

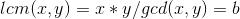
lcm(x,y)=x*y/gcd(x,y)=b

b=cij

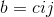
然后就证明了QAQ

代码：

#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#define up(i,x,y) for(int i = x;i <= y;i ++)
#define down(i,x,y) for(int i = x;i >= y;i --)
#define mem(a,b) memset((a),(b),sizeof(a))
#define mod(x) ((x)%MOD)
#define lson p<<1
#define rson p<<1|1
using namespace std;
typedef long long ll;
const int INF = 2147483640;
const double eps = 1e-8;
const int size = 1010;
const ll mod = 1e9+7;

inline void RD(int &x)
{
    x = 0;  char c; c = getchar();
    bool flag = 0;
    if(c == '-')    flag = 1;
    while(c < '0' || c > '9')   {if(c == '-')   {flag = 1;} c = getchar();}
    while(c >= '0' && c <= '9') x = (x << 1) + (x << 3) + c - '0',c = getchar();
}
ll gcd(ll a,ll b){return b == 0 ? a : gcd(b,a%b);}

ll a,b;
int main()
{
	while(scanf("%lld%lld",&a,&b) == 2)
	{
		ll gc = gcd(a,b);
		ll del = a*a-4*gc*b;
		if(del < 0)
		{
			puts("No Solution");
			continue;
		}
		ll sqdel = sqrt(del);
		if(sqdel*sqdel != del)
		{
			puts("No Solution");
			continue;
		}
		ll ans1 = (a + (ll)sqdel);
		ll ans2 = (a - (ll)sqdel);
		if(ans1 > 0 && ans1 % 2 == 0 && ans1/2 <= a)
		{
			ll ou1 = ans1/2;
			ll ou2 = a-ans1/2;
			if(ou1 > ou2)	swap(ou1,ou2);
			printf("%lld %lld\n",ou1,ou2);
		}
		else if(ans2 > 0 && ans2 % 2 == 0 && ans2/2 <= a)
		{
			ll ou1 = ans2/2;
			ll ou2 = a-ans2/2;
			if(ou1 > ou2)	swap(ou1,ou2);
			printf("%lld %lld\n",ou1,ou2);
		}
		else
		{
			puts("No Solution");
		}
	}
	return 0;
}

F - Binary Strings      <-题目链接 铜牌题

 Gym - 101845B

题目大意：给定两个长度相同的01串，同时定义两种操作：

操作1：把当前字符串最后一位移到第一位

操作2：翻转两个相邻的串

求进行最小的操作2次的数来把第一个变成第二个串，如果无法转化输出-1，如果可以输出操作2进行的次数

 

数据范围支持暴力，不过尽管能暴力还是要注意一个问题，第一个和最后一个也是可以交换的。

为什么？通过题意来看是不可以的，不过我们可以这样想，我先把最后一个字符移到第一位，把首位两个字符翻转,然后其他都不动，再进行操作1变成原来的位置顺序，就实现了交换。

所以暴力枚举所有可能的操作1的情况，然后每种情况暴力判断可不可以转换过去，如果可以就取ans = min(ans,nowcnt)，否则不操作.

代码很简单：

#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#define up(i,x,y) for(int i = x;i <= y;i ++)
#define down(i,x,y) for(int i = x;i >= y;i --)
#define mem(a,b) memset((a),(b),sizeof(a))
#define mod(x) ((x)%MOD)
#define lson p<<1
#define rson p<<1|1
#define shuchu(a) printf("qaq : %d",a); 
using namespace std;
typedef long long ll;
const int INF = 2147483640;
const double eps = 1e-8;
const int SIZE = 100010;
const ll mod = 1e9+7;

inline void RD(int &x)
{
    x = 0;  char c; c = getchar();
    bool flag = 0;
    if(c == '-')    flag = 1;
    while(c < '0' || c > '9')   {if(c == '-')   {flag = 1;} c = getchar();}
    while(c >= '0' && c <= '9') x = (x << 1) + (x << 3) + c - '0',c = getchar();
}

char s1[SIZE],s2[SIZE],s3[SIZE];
int len;
void routate()
{
	char c = s1[len];
	down(i,len-1,1)	s1[i+1] = s1[i];
	s1[1] = c;
	return ;
}
int ans = INF;
void check()
{
	int tot = 0;
	up(i,1,len)	s3[i] = s1[i];
	down(i,len,2)
	{
		if(s3[i] != s2[i])
		{
			if(s3[i] == '1')	s3[i] = '0';
			else	s3[i] = '1';
			if(s3[i-1] == '1')	s3[i-1] = '0';
			else	s3[i-1] = '1';
			tot ++;
		}
	}
	if(s3[1] == s2[1])	ans = min(ans,tot);
	//
	tot = 0;
	up(i,1,len)	s3[i] = s1[i];
	if(s3[1] == '1')	s3[1] = '0';
	else	s3[1] = '1';
	if(s3[len] == '1')	s3[len] = '0';
	else	s3[len] = '1';
	tot ++;
	down(i,len,2)
	{
		if(s3[i] != s2[i])
		{
			if(s3[i] == '1')	s3[i] = '0';
			else	s3[i] = '1';
			if(s3[i-1] == '1')	s3[i-1] = '0';
			else	s3[i-1] = '1';
			tot ++;
		}
	}
	if(s3[1] == s2[1])	ans = min(ans,tot);
	return ;
}
int main()
{
	scanf("%s",s1+1);
	scanf("%s",s2+1);
	len = strlen(s1+1);
	up(i,len+1,len*2)	s1[i] = s1[i - len];
	up(st,1,len)
	{
		//st为起点
		routate();
		check();
	}
	if(ans == INF)	printf("-1\n");
	else	printf("%d\n",ans);
	return 0;
}
/*
10110
11111
*/

G - Cryptography<-题目链接 签到题

 Gym - 101845C 

送分题。

题意很好读，不再赘述。

因为字符从33开始，32是空格 所以scanf%s读即可。

方法1：前向星建图，每个字母跑一遍spfa(),顺便记忆化一下。

方法2：大部分人都这么做的，弗洛伊德暴力n^3跑一遍任意两点最短路，但是，细节，细节，细节！

两点间可能给出多条边！！如果用邻接矩阵，一定要取最小值！！

代码：

#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#define up(i,x,y) for(int i = x;i <= y;i ++)
#define down(i,x,y) for(int i = x;i >= y;i --)
#define mem(a,b) memset((a),(b),sizeof(a))
#define mod(x) ((x)%MOD)
#define lson p<<1
#define rson p<<1|1
using namespace std;
typedef long long ll;
const int INF = 500000010;
const double eps = 1e-8;
const int size = 100010;
const ll mod = 1e9+7;

int dist[150][150];
int minn = INF,maxx = -1;
char s1[size],s2[size];
void flo()
{
	up(k,minn,maxx)
	{
		up(i,minn,maxx)
		{
			up(j,minn,maxx)
			{
				if(dist[i][k] != INF && dist[k][j] != INF)	dist[i][j] = min(dist[i][j],dist[i][k] + dist[k][j]);
			}
		}
	}
}
int n;
int main()
{
//	for(char i = 33;i <= 126;i ++)	cout<<(int)i<<" : "<>a>>b>>c;
	//		cout<

H - The Intriguing Obsession<-题目链接 铜牌题

 CodeForces - 869C 

参考博客：在这里

附图：

第四周周赛——三金三银两铜+签到_第1张图片

顺便 三棱柱是左边这东西 不是右边这东西23333333333

考场上没想出来确实值得自己反思一下

题解博客说的很好了，我就不多说了。有一个小技巧下一个题介绍

I - Anton and School - 2 <-题目链接 银牌题

 CodeForces - 785D

题目大意：给定一个括号序列，问有多少种()或者(())这种完整的包裹的括号子序列，不能是()()这种

思路：队友做的，膜大佬

我们想一个有左括号的地方，假设它左边有a个(     右边有b个)

那么这个点对答案的贡献是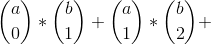：\binom{a}{0}*\binom{b}{1} + \binom{a}{1}*\binom{b}{2} + ……......

（解释一下 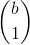\binom{a}{0}\binom{b}{1}代表只选当前左括号，从右边右边右括号中选一个 ）

（\binom{a}{1}\binom{b}{2}代表从当前位置左边左括号选一个，从右边右括号里选两个）

然后所有合法的值得和就是它这个位置对答案的贡献

然后，你以为这样就完了吗233

然后咋整啊= = ——进入挂机模式zzz

队友无聊翻书：卧槽！！！你猜我找到了什么！！！！

史上最刺激AC题目

代码：

#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#define up(i,x,y) for(int i = x;i <= y;i ++)
#define down(i,x,y) for(int i = x;i >= y;i --)
#define mem(a,b) memset((a),(b),sizeof(a))
#define mod(x) ((x)%MOD)
#define lson p<<1
#define rson p<<1|1
using namespace std;
typedef long long ll;
const int INF = 2147483640;
const double eps = 1e-8;
const int SIZE = 200010;
const ll mod = 1000000007;

inline void RD(int &x)
{
    x = 0;  char c; c = getchar();
    bool flag = 0;
    if(c == '-')    flag = 1;
    while(c < '0' || c > '9')   {if(c == '-')   {flag = 1;} c = getchar();}
    while(c >= '0' && c <= '9') x = (x << 1) + (x << 3) + c - '0',c = getchar();
}
int l[SIZE],r[SIZE];//左边有几个左括号 右边有几个右括号 
char s[SIZE];
ll inv[SIZE];
ll facinv[SIZE],fac[SIZE];//逆元阶乘表 阶乘表 
void init()
{
	fac[0] = facinv[0] = 1;
	inv[1]=1;  
    for(int i = 2; i <= 200000; i++)	inv[i]=(mod-mod/i) * inv[mod%i] % mod;
	facinv[1] = inv[1];
	for(int i = 2; i <= 200000; i++)	facinv[i] = facinv[i-1] * inv[i] % mod;
	fac[1] = 1;
	for(int i = 2; i <= 200000; i++)	fac[i] = fac[i-1] * i % mod;
}

ll C(ll a,ll b)
{
	return ((fac[a] * facinv[b])%mod * facinv[a-b])%mod;
}

int main()
{
	init();
	scanf("%s",s);
	int len = strlen(s);
	l[0] = (s[0] == '(' );
	up(i,1,len-1)
	{
		l[i] = l[i-1] + (s[i] == '(' );
	//	printf("%d : %d\n",i,l[i]);
	}
	r[len-1] = s[len-1] == ')';
	down(i,len-2,0)	r[i] = r[i+1] + (s[i] == ')' );
	ll ans = 0;
	up(i,0,len-1)
	{
		if(s[i] == '(' )
		{
		//	printf("l,r : %d %d\n",l[i],r[i]);
			ans = (ans + C(l[i]-1+r[i],r[i]-1))%mod;
		//	printf("ans : %d\n",ans);
		}
		
	}
	printf("%I64d\n",ans);
	return 0;
}

J - Purifying Machine<-题目链接 铜牌题

 POJ - 2724

题目大意：自己百度2333

思路：强行把每个带*的都拆开。

然后对每个数再拆成两个，如果一个数可以通过改变二进制的某一位变成另一个数，比如a,b两个点，然后a->b^1和b->a^1建边

然后这就是个二分图了，相当于求最大边覆盖，通过定理我们知道就是求最大匹配。

但是，我为什么wr了一上午+半个下午呢？

我们来看这个最大匹配，模拟样例我们可以看出来匹配一般是一对一对的匹配。所以最后要除以2

但是，其实……有匹配数为奇数的时候。。这个时候答案加的就是匹配数/2+1了，因为那个单独的1无法成对匹配。

所以最终答案要分一下类（也可以不用分类，直接ans += pipei/2 + pipei%2;

#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#define up(i,x,y) for(int i = x;i <= y;i ++)
#define down(i,x,y) for(int i = x;i >= y;i --)
#define mem(a,b) memset((a),(b),sizeof(a))
#define mod(x) ((x)%MOD)
#define lson p<<1
#define rson p<<1|1
using namespace std;
typedef long long ll;
const int INF = 2147483640;
const double eps = 1e-8;
const int SIZE = 23330;
const ll mod = 1e9+7;

struct Edge{int to;}edges[SIZE];
int head[SIZE],next[SIZE],tot;
void build(int f,int t)
{
	edges[++tot].to = t;
	next[tot] = head[f];
	head[f] = tot;
}
bool vis[SIZE];
int connect[SIZE];
int bian;
bool dfs(int u)
{
	for(int i = head[u];i;i = next[i])
	{
		int v = edges[i].to;
		if(!vis[v])
		{
			vis[v] = 1;
			if(!connect[v] || dfs(connect[v]))
			{
				connect[v] = u;
				return true;
			}
		}
	}
	return false;
}
char s[SIZE];
int num[SIZE];
bool quchong[SIZE]; 
int cnt,n,m;
void init()
{
	mem(edges,0);
	mem(head,0);
	mem(next,0);
	tot = 0;
	
	mem(connect,0);
	bian = 0;//二分图最大边覆盖 
	
	mem(num,0);
	mem(quchong,0);
	cnt = 0;//数的个数 
	mem(vis,0);
}
bool check(int x,int y)
{
	int dif = 0; 
	for(int i = 0;i <= 11;i ++)
	{
		int a = (1 << i);
		if((x&a) != (y&a))	dif ++;
		if(dif > 1)	break; 
	}
	if(dif == 1)	return true;
	return false;
}
int main()
{
	freopen("case.txt","r",stdin);
	freopen("wode.txt","w",stdout);
	while(scanf("%d%d",&n,&m) && n && m)
	{
		init();
		up(i,1,m)
		{
			scanf("\n%s",s);
			int a = 0,b = -1;
			bool flag = 0;
			up(j,0,n-1)
			{
				if(s[j] == '*')
				{
					b = a;
					a = (a << 1) + 1;
					b = (b << 1);
					flag = 1;
				}
				else
				{
					a = ((a << 1) | (s[j] - '0'));
					if(flag)	b = ((b << 1) | (s[j] - '0'));
				}
			}
			if(!quchong[a])
			{
				num[cnt ++] = a;
				quchong[a] = 1;
			}
			if(b != -1 && !quchong[b])
			{
				num[cnt ++] = b;//从零开始 
				quchong[b] = 1;
			}
		}
	//	printf("cnt : %d\n",cnt); 
	//	printf("%d %d %d %d\n",num[0],num[1],num[2],num[3]);
		up(i,0,cnt-1)
		{
			up(j,0,cnt-1)
			{
				if(i == j)	continue ;
				int a = num[i];
				int b = num[j];
				if(check(a,b))
				{
		//			printf("i,j : %d %d\n",i,j);
					build(i,j*2+1);
				}
			}
		}
		for(int i = 0;i < cnt;i ++)
		{
			memset(vis,0,sizeof(vis));
			if(dfs(i))	bian ++;
		}
	//	printf("bian : %d\n",bian); 
		printf("%d\n",bian/2 + bian%2 + (cnt - bian));
	}
	return 0;
}

/*
3 6
*01
100
011
1*1
110
001
0 0

1 2
1
0
0 0

3 3
1*1
100
011

*/

其他题暂时没看，目测D,K还是可做的题，都是银牌题左右的题把。

你可能感兴趣的:(ACM比赛,杭电,poj,Codeforces)

  • 勇士赢了，我把掌声给了骑士 复角度的生活
    今天，不参加高考，只看NBA总决赛第三场的较量。这么说有点得罪高考生了，不过我没有当他们面秀，也没有跑到考点外面得瑟，所以我内心毫无波澜。毫无疑问，考场里不乏骑士和勇士球迷，在紧张作答语文考卷同时还心系着球队，不过我希望今天的比赛不会让你们有所分心，毕竟高考不会像比赛录像那样可以再来。今天，好像起来赶考一样，我起得很早，然而事实是睡不着，挺郁闷的，又不是我高考，我紧张什么？九点我并没有准时打开浏览
  • 《Python数据分析实战终极指南》 xjt921122 python数据分析开发语言
    对于分析师来说，大家在学习Python数据分析的路上，多多少少都遇到过很多大坑**，有关于技能和思维的**：Excel已经没办法处理现有的数据量了，应该学Python吗？找了一大堆Python和Pandas的资料来学习，为什么自己动手就懵了？跟着比赛类公开数据分析案例练了很久，为什么当自己面对数据需求还是只会数据处理而没有分析思路？学了对比、细分、聚类分析，也会用PEST、波特五力这类分析法，为啥
  • 最超值的Mac——Mac mini 初心么么哒
    你知道最超值的Mac是什么吗？自2005年以来，Macmini一直是Apple台式机产品线中的主要产品。最初推出是为了让对Mac好奇的Mac进入Apple生态系统的一种简单方式，现在新的AppleSiliconMacmini可能是任何寻找新Mac的人的最有吸引力的购买。什么是AppleSiliconMacmini？M1Macmini是Apple最小的台式电脑，同时也是最快的台式电脑之一。最新型号由
  • 2022-11-25 疫情卷土而来 快乐微笑每一天
    原计划本周因比赛休息两天半，结果一个阳性患者疫情转变了所有，轮休课表换掉，继续周五上课；比赛顺延，假期顺延，相对应确诊病例所在区域封闭。这疫情何时是一个尽头，谁也无法知晓，唯有进出带好口罩，保护自己，方能战胜疫情。疫情无情，人间温暖，期待疫情早日过去，大地重返平安和谐。
  • Codeforces Round 972 (Div. 2) A-C 题解 AKDreamer_HeXY Codeforces比赛题解c++算法动态规划数据结构贪心算法
    本来以为B2难度会1900什么的，结果感觉1200还没有，先做的B1，后悔了QwQ关于我现场没切出C这件事……现场排名：A.SimplePalindrome题意构造一个长度为nnn的字符串，只包含aeiou五种字母，需要使得构造出来的字符串所包含的回文子序列数量最小思路当n≤5n\le5n≤5时，只要555个字母不重复出现都是最优情况当n>5n>5n>5时，可以证明：把相同字母放在一起是最优情况：
  • 稍微落后的人更容易被激励成长 有杕之杜
    今日纯分享。图片发自App沃顿商学院市场营销学教授乔纳·伯杰在接受《哈佛商业评论》采访时，介绍了他的一项研究。伯杰教授告诉参加实验的人，他们在跟隔壁房间的另一个人比赛打字速度，获胜的人有金钱奖励。一轮比赛之后，伯杰给了这些人不同的反馈，有的人被告知远远落后竞争对手，有的人被告知稍稍落后，还有的人被告知不相上下或者略微领先。结果只有那些被告知“稍微落后”的人，在第二轮中速度明显提高，而且总体来说，这
  • 详解mybatis的一二级缓存以及缓存失效原因 仰望天花板 缓存数据库mybatisjavamysql
    数据库的大部分场景下是从磁盘读取，如果数据从内存进行读取，速度较比磁盘要快得多。但因为内存的容量有限，所以一般只会把使用和查询较多的数据缓存起来，以便快速反应，其他使用率不太多的继续存放在磁盘。mybatis分为一级缓存和二级缓存1.一级缓存一级缓存存放在SqlSqeeion上，默认开启1.1pojo@DatapublicclassRole{privateLongid;privateStringr
  • 向着明亮那方12.7 向着明亮那方的我们
    【水晶泥的妙用】在地上捡到一滩水晶泥，本想扔进垃圾桶，发现水晶泥上附着了些许蓝色钢笔墨水。我脑洞大开，水晶泥可不可以用来处理钢笔墨渍呢？正好垃圾桶那面瓷砖墙上有蓝色钢笔水痕迹，我用水晶泥沾了沾墨迹，很轻易地把墨色粘了下来，好干净。【长跑报名】我让同学们自愿报名参加冬季长跑比赛，课间将名字报给班长。班长把名字统计在本子上，把本子拿来给我看：“老师，我晚上回去给你做张电子表，发给你。”看来班长又学了新
  • WORD批量转换器MultiDoc Converter uolian 工作word
    WORD批量转换器MultiDocConverterhttps://www.52pojie.cn/thread-1318745-1-1.html可批量将doc、docx等文件格式转成doc、docx、pdf、rtf、txt、html、epub等格式。安装包下载地址：https://wws.lanzouj.com/irvVbiz0pkd最终下载文件打包地址（未作成单文件，不确定是否可以直接使用）：h
  • 全运会结束了除了闭幕式无亮点外对西安发展大有裨益 新心芯达人
    前言昨天是最后一个比赛日，山东代表团单日揽4金，最后以58金55银47铜，总计160枚奖牌的成绩位列奖牌榜第一的位置，这已经是山东连续第四届全运会取得奖牌榜第一的成绩，以绝对的优势达成了四连冠成就，山东属实厉害！广东在本届全运会中也拼尽了全力，在26号的最后一个比赛日，狂揽6金，最后以54金，32银，56铜，总计142枚奖牌位列奖牌榜第二的位置，虽然最后一个比赛日爆发连夺6金，最后还是没有撼动山东
  • 72称体重 作者：陈瑄仪 家庭教育CEO
    2019年5月1日星期三大雨昭阳区今天我们开始准备明天的比赛，教练说早上8:00叫我们到市委党校集合，爸爸很早就送我到市委党校了，我在那里等了好久，教练还没来，我就在那里跑步，跑了十几圈教练还没有来又跑几圈教练还没来，我们就觉得奇怪了，教练不会在家里睡懒觉吧，我们又跑了几圈才休息。等教练来了我们就去称重体重，第一次称，没过，我急了，教练说我超了0.3公斤，让我去跑了几圈重量才减下来，明明之前几天只
  • 2019-11-29晨间日记 麦新
    今天是什么日子起床：6:00就寝：23:30天气：晴朗心情：平静纪念日：第二场比赛叫我起床的不是闹钟是梦想年度目标及关键点：国考考研本月重要成果：学习今日三只青蛙/番茄钟点评作业出镜点评夜班成功日志-记录三五件有收获的事务出镜点评点评作业夜班财务检视-1人际的投入来回跑～开卷有益-学习/读书/听书《孔子》健康与饮食今日步数：8000+好习惯打卡早晚打卡阅读打卡听书打卡社群打卡
  • 特雷-杨表现出色，比肩詹姆斯，库里 Allen196
    特雷-杨得到35分11次助攻。从2000年以后只有两个新秀可以打出这样的数据（至少35分，10次助攻），他们的名字是：史蒂芬-库里，勒布朗-詹姆斯。现在亚特兰大老鹰队的特雷-杨加入了他们的行列，在对阵克里夫兰骑士队的比赛中，他拿到了35分，11次助攻帮助老鹰队取得胜利，同时也是老鹰队主教练罗伊德-皮尔斯作为NBA主教练的首场胜利。揭幕战战胜尼克斯，第二场战胜防守强硬的灰熊后，杨再次帮助球队战胜了骑
  • D15 论语学习笔记 许小兔Angelina
    悟：上级对下级的宽容：凡事成定局，就不你说了；已接近完结的事，也没必要匡正和挽回了；既然是过去的事，也没必要追究得失和责任了。对待孩子教育也是，不用“问责制”，这样容易让孩子因为害怕担责而说谎。应当循循善诱，避免再犯错才是最重要的。3.16：【原文】子曰：“射不主皮，为力不同科，古之道也。”【译文】孔子说：“射箭比赛不以射透为主，而主要看是否射得准确，因为人的力量不同，自古如此。”3.17：【原文
  • Codeforces Round 969 (Div. 2) C. Dora and C++ （裴蜀定理） 致碑前繁花 刷题记录c语言c++开发语言
    什么？竟然是裴蜀定理。。。由于这里给出了a和b两个数，我们或许可以想到使用同样是需要给出两个定值的裴蜀定理，即：如果给定xxx和yyy，那么一定有ax+by=gcd(x,y)ax+by=gcd(x,y)ax+by=gcd(x,y)。所以在这时候我们就可以让输入的所有数都去对gcd(a,b)gcd(a,b)gcd(a,b)取模，这样就能够得到所有数的最简形式（可以当成是让所有数尽可能消去aaa和bb
  • MyBatis系统学习（一）——项目结构及其含义 OEC小胖胖 MyBatismybatis学习web后端
    1.MyBatis简介MyBatis是一款优秀的持久层框架，它通过SQL映射的方式实现Java对数据库操作的映射，既保留了SQL语句的灵活性，也简化了代码的编写。在一个MyBatis项目中，核心部分主要有：配置文件（mybatis-config.xml）映射文件（Mapper.xml）实体类（Entity/POJO）接口类（Mapper接口）MyBatis会话工厂（SqlSessionFactor
  • 中国男篮：15万赛后评分，赵继伟第三，赵睿3.8分倒数第一 体娱荒原
    在某体育社交软件中，有15万人之多为中国男篮第二场比赛进行点评，我们一起来看看他们的评分排名。这场比赛有12人出场，全部球员都有得分进账。吴前9.9分，这场比赛他拿到全队最高的18分还有4篮板3助攻3抢断，虽然也有3次失误和5次犯规，但是瑕不掩瑜，特别是最后一节单节得到10分跟赵继伟的连线帮助球队逆转对手赢得一场胜利，他的发挥至关重要，要知道对手对他也有研究，基本上都是贴身防守，持球还有夹击，吴前
  • 平昌冬奥，人生竞赛不要给对手和裁判任何机会 小猫_003e
    如火如荼的平昌冬奥会拉下了帷幕，但是自从某年的伦敦奥运会之后，我们中国队自从好像就“最爱干犯规的事儿”。2月20日，短道速滑女子3000米接力赛，可以说是相当令人痛心了。比赛中，韩国队交接棒失误“扑街”，阻拦了加拿大队，带来的连锁反应也影响了中国队。中国队以微弱劣势落后韩国队，第二个冲线！韩国队这次失误犯规那么明显，应该唱费玉清的我送你离开千里之外。但···最终赛场上裁判宣布：韩国队冠军，中国队、
  • 周记15 安诗雨
    星期天回学校的时候，发现寝室里有好几只臭屁虫。星期一的电学很难，数学也非常难，让我感到非常吃力。历史比赛日期就在11月29日，也就是我的生日。唉，过生日去比赛，我好难受。不仅如此，还是高手对决……老师希望“保三争二冲一”，我也希望来一个一等奖，这样多光荣，也证明了自己的实力。不管怎么样，要全力以赴。星期二我们进行了电子技能实训期中考试。对我来说，简直不要太轻松。无非就是拿万用表测电阻值，顺带读出来
  • 【足坛简讯】9月2日足坛简讯及比赛预告 神州足球
    【足坛简讯】9月2日足坛简讯及比赛预告9月2日足坛简讯与比赛预告比赛结果✍️意甲第3轮：十人米兰2-1罗马三连胜领跑莱奥凌空斩吉鲁点射托莫里染红✍️德甲第3轮：两连平！多特连丢两球2-2遭升班马海登海姆扳平布兰特凌空斩✍️沙特联：米特洛维奇戴帽本泽马破门新月连入三球4-3逆转吉达联合✍️热身赛：中国国奥1-0土库曼斯坦国奥，艾菲尔丁制胜球国内足坛✍️明日之星足球赛：上海队点球憾负曼城，大阪樱花蔚山
  • 都2024年了，还在问网络安全怎么入门，气得我当场脑血栓发作 网安大师兄 web安全网络安全网络安全学习
    前言本人从事网路安全工作12年，曾在2个大厂工作过，安全服务、售后服务、售前、攻防比赛、安全讲师、销售经理等职位都做过，对这个行业了解比较全面。下面就开始进入正题，如何从一个萌新一步一步进入网络安全行业。正题首先,在准备进入这个行业之前，我们要问一下我们的内心，工作千千万，为什么要想进入这个行业？相信每个人的答案都不一样，有的人会说，这个行业整体上比其他行业赚钱多，有的人会说特别喜欢技术，想钻研一
  • 第十二章〈一〉 汝此一生1985
    接下来的运动会时光便是和东美一起度过。两人时不时就去超市买上一大袋东西，提着一大袋东西然后坐在操场上看着比赛消磨时光。下午两三点时刻，太阳很大，笼罩了整个操场，晒得人只想睡觉。秦嘉杨在篮球场挥洒热汗，东美躺在林召航腿上和林召航一起听着歌。拒绝去看秦嘉杨比赛，“我可不想看见他和他那个情人的亲密互动。”说着忿忿填进嘴里一个薯片。林召航拔下耳机，“哪来的情人？”东美：“姓篮名球”东美的嘴巴变成了“0”形
  • Dev-C++头文件小Bug 蒟蒻pzjdsg666 bugc语言c++
    Dev-C++应该是大家最常用的C++软件了吧，但它有几个小Bug。1、“万能头”众所周知，“万能头”在官方比赛中不能使用（你要用没人拦着你~呵呵），但在Dev-C++可以使用。所以，我们可以省掉好多头文件！如下：#includeusingnamespacestd;2、C语言头文件在Dev-C++中，你竟然可以使用C语言头文件（惊不惊喜~意不意外~）如下：#include3、iostream竟然包
  • 跃迁第一天 师者之写道
    《跃迁》你怎么也想不到火车在替代马车的时候，很多人嘲笑火车，甚至夸张地和火车比赛，直到今天，马车被淘汰了，更别说有能赶上马车的火车了！时代在发展，我们稍微不学习，不改变就可能永远地被淘汰在世界的某一个角落里。今天我用拆书法拆了我自己。
  • 周二竞足：塞维利亚力争小胜巴萨，亚特兰大击败热那亚如探囊取物 阿东侃球
    昨日赛事回顾：富勒姆对阵谢菲尔德联这场很简单，整体方向是正确的，但是谢菲联在开局3分钟进了1个球后，富勒姆竟然没能追平，全场就只有这1个进球，有点可惜。莱万特和巴伦西亚这一场比赛简直就是折磨人，上半场莱万特2-1领先，下半场却被反攻最终3-4结束，硬生生的打出了胜负的战果，着实惊到了我。周二003意甲：热那亚VS亚特兰大比赛时间：2021-12-2203:45基本面分析：热那亚联赛1胜7平10负积
  • 当姨妈遇见马拉松赛事，该怎么破 语非年
    图片发自App凌晨4:30分匆匆洗漱出门，到5:10分集合点与团长、许总车自驾前往参赛地（漳州市华安县），车上听说参赛点大雨倾盆，本来就有心无意参赛的（没雨就跑，有雨弃赛），果不其然在进入华安县的时候就遇瓢泼大雨，于是与如风大神们说笑着，若到起跑点还是这般大雨就弃赛。因都身体抱恙。所幸，天工不负有心人，到达目的地存包直到开跑，雨奇迹般的停了。临近比赛的前三天正好生理期，在纠结去还是不去的时候，内心
  • 2022年3月23日复盘 凤晴天
    工作方面：今天过来开始伎钢筋的结算单。然后开始做模板木方的结算单。开始加昨天钢管扣件对账缺的部分，晚上过来加班，又把那个需求总计划给上传了一下。25号要上传创效和限额领料资料。学习方面：1.秘密的话，还是没有怎么听他们社群里面的分享。2、21天演讲训练营，今天是总决赛及结营仪式。因为加班也没有听他们的比赛。但是看群里边发的就是军人的，感觉军人的气概，那种气魄非常强。3.小a的话已经开始拉10天训练
  • 扎吉托娃：我高兴自己没有让团队失望 云游四方的旅人
    阿莉娜·扎吉托娃赛后采访时表示，自己满意自己没有让团队失望。“我滑得好，过程非常高兴，克服自己的焦虑，高兴，我没有让团队失望。”“我告诉自己事实上我在训练中一切都做很好，所有的动作都做好了，为什么我不能在比赛中做好呢？”
  • SpringBoot项目 俺叫啥好嘞 spring系列springspringboot
    SpringBoot项目大概分为四层：（1）DAO层：包括XxxMapper.java(数据库访问接口类)，XxxMapper.xml(数据库链接实现)；（这个命名，有人喜欢用Dao命名，有人喜欢用Mapper，看个人习惯了吧）（2）Bean层：也叫model层，模型层，entity层，实体层，就是数据库表的映射实体类，存放POJO对象；（3）Service层：也叫服务层，业务层，包括XxxSer
  • 惊喜！国足福将被施密特神奇复活，他的作用比肩外援，里皮开心了 枫桥落夜
    2018年7月22日晚，北京工人体育场进行了一场精彩激烈的新京津德比大战，由北京中赫国安对阵天津权健。这是一场强强对话，天津权健是上赛季的中超第三名，亚冠也打进了8强，实力强劲。而北京国安联赛已经11轮不败，领跑积分榜，本赛季是奔着冠军而去的。北京中赫国安本场比赛是有非常大的优势的，因为他们的内外援齐整，巴西国脚奥古斯托从世界杯回来也已经归队，而权健的维特赛尔和莫德斯特都还没有回来，只能有两外援上
  • 矩阵求逆（JAVA）利用伴随矩阵 qiuwanchi 利用伴随矩阵求逆矩阵
    package gaodai.matrix; import gaodai.determinant.DeterminantCalculation; import java.util.ArrayList; import java.util.List; import java.util.Scanner; /** * 矩阵求逆(利用伴随矩阵) * @author 邱万迟
  • 单例（Singleton）模式 aoyouzi 单例模式Singleton
    3.1           概述 如果要保证系统里一个类最多只能存在一个实例时，我们就需要单例模式。这种情况在我们应用中经常碰到，例如缓存池，数据库连接池，线程池，一些应用服务实例等。在多线程环境中，为了保证实例的唯一性其实并不简单，这章将和读者一起探讨如何实现单例模式。 3.2
  • [开源与自主研发]就算可以轻易获得外部技术支持,自己也必须研发 comsci 开源
          现在国内有大量的信息技术产品，都是通过盗版，免费下载，开源，附送等方式从国外的开发者那里获得的。。。。。。        虽然这种情况带来了国内信息产业的短暂繁荣，也促进了电子商务和互联网产业的快速发展，但是实际上，我们应该清醒的看到，这些产业的核心力量是被国外的
  • 页面有两个frame,怎样点击一个的链接改变另一个的内容 Array_06 UIXHTML
    <a src="地址"  targets="这里写你要操作的Frame的名字" />搜索 然后你点击连接以后你的新页面就会显示在你设置的Frame名字的框那里 targerts="",就是你要填写目标的显示页面位置 ===================== 例如： <frame src=&
  • Struts2实现单个/多个文件上传和下载 oloz 文件上传struts
    struts2单文件上传：     步骤01:jsp页面 <!--在进行文件上传时，表单提交方式一定要是post的方式，因为文件上传时二进制文件可能会很大，还有就是enctype属性，这个属性一定要写成multipart/form-data，不然就会以二进制文本上传到服务器端--> 　　<form action="fileUplo
  • 推荐10个在线logo设计网站 362217990 logo
    在线设计Logo网站。 1、http://flickr.nosv.org（这个太简单） 2、http://www.logomaker.com/?source=1.5770.1 3、http://www.simwebsol.com/ImageTool 4、http://www.logogenerator.com/logo.php?nal=1&tpl_catlist[]=2 5、ht
  • jsp上传文件 香水浓 jspfileupload
    1. jsp上传 Notice： 1. form表单 method 属性必须设置为 POST 方法 ，不能使用 GET 方法 2. form表单 enctype 属性需要设置为 multipart/form-data 3. form表单 action 属性需要设置为提交到后台处理文件上传的jsp文件地址或者servlet地址。例如 uploadFile.jsp 程序文件用来处理上传的文
  • 我的架构经验系列文章 - 前端架构 agevs JavaScriptWeb框架UIjQuer
    框架层面：近几年前端发展很快，前端之所以叫前端因为前端是已经可以独立成为一种职业了，js也不再是十年前的玩具了，以前富客户端RIA的应用可能会用flash/flex或是silverlight，现在可以使用js来完成大部分的功能，因此js作为一门前端的支撑语言也不仅仅是进行的简单的编码，越来越多框架性的东西出现了。越来越多的开发模式转变为后端只是吐json的数据源，而前端做所有UI的事情。MVCMV
  • android ksoap2 中把XML(DataSet) 当做参数传递 aijuans android
    我的android app中需要发送webservice ，于是我使用了 ksop2 进行发送，在测试过程中不是很顺利,不能正常工作.我的web service 请求格式如下     [html]  view plain copy   <Envelope xmlns="http://schemas.
  • 使用Spring进行统一日志管理 + 统一异常管理 baalwolf spring
    统一日志和异常管理配置好后，SSH项目中，代码以往散落的log.info() 和 try..catch..finally 再也不见踪影！ 统一日志异常实现类： [java]  view plain copy   package com.pilelot.web.util;      impor
  • Android SDK 国内镜像 BigBird2012 android sdk
    一、镜像地址： 1、东软信息学院的 Android SDK 镜像，比配置代理下载快多了。 配置地址， http://mirrors.neusoft.edu.cn/configurations.we#android 2、北京化工大学的： IPV4:ubuntu.buct.edu.cn  IPV4:ubuntu.buct.cn IPV6:ubuntu.buct6.edu.cn
  • HTML无害化和Sanitize模块 bijian1013 JavaScriptAngularJSLinkySanitize
    一.ng-bind-html、ng-bind-html-unsafe         AngularJS非常注重安全方面的问题，它会尽一切可能把大多数攻击手段最小化。其中一个攻击手段是向你的web页面里注入不安全的HTML，然后利用它触发跨站攻击或者注入攻击。         考虑这样一个例子，假设我们有一个变量存
  • [Maven学习笔记二]Maven命令 bit1129 maven
    mvn compile compile编译命令将src/main/java和src/main/resources中的代码和配置文件编译到target/classes中，不会对src/test/java中的测试类进行编译 MVN编译使用 maven-resources-plugin:2.6:resources maven-compiler-plugin:2.5.1:compile &nbs
  • 【Java命令二】jhat bit1129 Java命令
    jhat用于分析使用jmap dump的文件，，可以将堆中的对象以html的形式显示出来，包括对象的数量，大小等等，并支持对象查询语言。 jhat默认开启监听端口7000的HTTP服务，jhat是Java Heap Analysis Tool的缩写 1. 用法： [hadoop@hadoop bin]$ jhat -help Usage: jhat [-stack <bool&g
  • JBoss 5.1.0 GA:Error installing to Instantiated: name=AttachmentStore state=Desc ronin47
    进到类似目录 server/default/conf/bootstrap，打开文件 profile.xml找到： Xml代码<bean    name="AttachmentStore"  class="org.jboss.system.server.profileservice.repository.AbstractAtta
  • 写给初学者的6条网页设计安全配色指南 brotherlamp UIui自学ui视频ui教程ui资料
    网页设计中最基本的原则之一是，不管你花多长时间创造一个华丽的设计，其最终的角色都是这场秀中真正的明星——内容的衬托     我仍然清楚地记得我最早的一次美术课，那时我还是一个小小的、对凡事都充满渴望的孩子，我摆放出一大堆漂亮的彩色颜料。我仍然记得当我第一次看到原色与另一种颜色混合变成第二种颜色时的那种兴奋，并且我想，既然两种颜色能创造出一种全新的美丽色彩，那所有颜色
  • 有一个数组，每次从中间随机取一个，然后放回去，当所有的元素都被取过，返回总共的取的次数。写一个函数实现。复杂度是什么。 bylijinnan java算法面试
    import java.util.Random; import java.util.Set; import java.util.TreeSet; /** * http://weibo.com/1915548291/z7HtOF4sx * #面试题#有一个数组，每次从中间随机取一个，然后放回去，当所有的元素都被取过，返回总共的取的次数。 * 写一个函数实现。复杂度是什么
  • struts2获得request、session、application方式 chiangfai application
    1、与Servlet API解耦的访问方式。 a.Struts2对HttpServletRequest、HttpSession、ServletContext进行了封装，构造了三个Map对象来替代这三种对象要获取这三个Map对象，使用ActionContext类。 ----->   package pro.action; import java.util.Map; imp
  • 改变python的默认语言设置 chenchao051 python
    import sys sys.getdefaultencoding()  可以测试出默认语言，要改变的话，需要在python lib的site-packages文件夹下新建： sitecustomize.py， 这个文件比较特殊，会在python启动时来加载，所以就可以在里面写上： import sys sys.setdefaultencoding('utf-8') &n
  • mysql导入数据load data infile用法 daizj mysql导入数据
    我们常常导入数据！mysql有一个高效导入方法，那就是load data infile 下面来看案例说明 基本语法： load data  [low_priority] [local] infile 'file_name txt' [replace | ignore] into table tbl_name [fields [terminated by't'] [OPTI
  • phpexcel导入excel表到数据库简单入门示例 dcj3sjt126com PHPExcel
    跟导出相对应的，同一个数据表，也是将phpexcel类放在class目录下，将Excel表格中的内容读取出来放到数据库中 <?php error_reporting(E_ALL); set_time_limit(0); ?> <html> <head> <meta http-equiv="Content-Type"
  • 22岁到72岁的男人对女人的要求 dcj3sjt126com
    22岁男人对女人的要求是：一，美丽，二，性感，三，有份具品味的职业，四，极有耐性，善解人意，五，该聪明的时候聪明，六，作小鸟依人状时尽量自然，七，怎样穿都好看，八，懂得适当地撒娇，九，虽作惊喜反应，但看起来自然，十，上了床就是个无条件荡妇。 32岁的男人对女人的要求，略作修定，是：一，入得厨房，进得睡房，二，不必服侍皇太后，三，不介意浪漫蜡烛配盒饭，四，听多过说，五，不再傻笑，六，懂得独
  • Spring和HIbernate对DDM设计的支持 e200702084 DAO设计模式springHibernate领域模型
    A：数据访问对象     DAO和资源库在领域驱动设计中都很重要。DAO是关系型数据库和应用之间的契约。它封装了Web应用中的数据库CRUD操作细节。另一方面，资源库是一个独立的抽象，它与DAO进行交互，并提供到领域模型的“业务接口”。    资源库使用领域的通用语言，处理所有必要的DAO，并使用领域理解的语言提供对领域模型的数据访问服务。
  • NoSql 数据库的特性比较 geeksun NoSQL
    Redis 是一个开源的使用ANSI C语言编写、支持网络、可基于内存亦可持久化的日志型、Key-Value数据库，并提供多种语言的API。目前由VMware主持开发工作。   1. 数据模型 作为Key-value型数据库，Redis也提供了键（Key）和值（Value）的映射关系。除了常规的数值或字符串，Redis的键值还可以是以下形式之一： Lists （列表） Sets
  • 使用 Nginx Upload Module 实现上传文件功能 hongtoushizi nginx
    转载自： http://www.tuicool.com/wx/aUrAzm   普通网站在实现文件上传功能的时候，一般是使用Python，Java等后端程序实现，比较麻烦。Nginx有一个Upload模块，可以非常简单的实现文件上传功能。此模块的原理是先把用户上传的文件保存到临时文件，然后在交由后台页面处理，并且把文件的原名，上传后的名称，文件类型，文件大小set到页面。下
  • spring-boot-web-ui及thymeleaf基本使用 jishiweili springthymeleaf
    视图控制层代码demo如下：   @Controller @RequestMapping("/") public class MessageController { private final MessageRepository messageRepository; @Autowired public MessageController(Mes
  • 数据源架构模式之活动记录 home198979 PHP架构活动记录数据映射
    hello!架构 一、概念 活动记录（Active Record）：一个对象，它包装数据库表或视图中某一行，封装数据库访问，并在这些数据上增加了领域逻辑。 对象既有数据又有行为。活动记录使用直截了当的方法，把数据访问逻辑置于领域对象中。   二、实现简单活动记录 活动记录在php许多框架中都有应用，如cakephp。 <?php /** * 行数据入口类 *
  • Linux Shell脚本之自动修改IP pda158 linuxcentosDebian脚本
    作为一名 Linux SA，日常运维中很多地方都会用到脚本，而服务器的ip一般采用静态ip或者MAC绑定，当然后者比较操作起来相对繁琐，而前者我们可以设置主机名、ip信息、网关等配置。修改成特定的主机名在维护和管理方面也比较方便。如下脚本用途为：修改ip和主机名等相关信息，可以根据实际需求修改，举一反三！ #!/bin/sh #auto Change ip netmask ga
  • 开发环境搭建 独浮云 eclipsejdktomcat
           最近在开发过程中，经常出现MyEclipse内存溢出等错误，需要重启的情况，好麻烦。对于一般的JAVA+TOMCAT项目开发，其实没有必要使用重量级的MyEclipse，使用eclipse就足够了。尤其是开发机器硬件配置一般的人。         &n
  • 操作日期和时间的工具类 vipbooks 工具类
       大家好啊，好久没有来这里发文章了，今天来逛逛，分享一篇刚写不久的操作日期和时间的工具类，希望对大家有所帮助。 /* * @(#)DataFormatUtils.java 2010-10-10 * * Copyright 2010 BianJing,All rights reserved. */ package test; impor
按字母分类： ABCDEFGHIJKLMNOPQRSTUVWXYZ其他