Dijkstra算法及其堆优化代码详解

迪杰斯特拉算法解决的是带权重的有向图上单源最短路径问题，该算法要求所有边的权重都为非负值，其在运行过程中维持的关键信息是一组节点集合S。算法重复从结点集V-S中选择最短路径估计最小的结点u，将u加入到集合S，然后对所有从u发生的边进行松弛，运行结束后，从源节点到集合S中每个结点之间的最短路径已经被找到。

下面，通过一个实例讲解该过程！

1 实例讲解

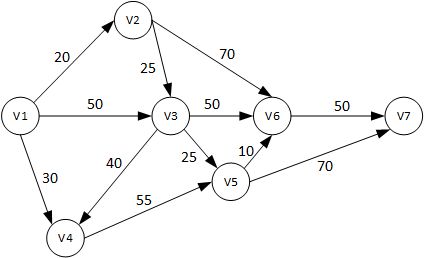
如图，是一个有向无环图，假定出发点为V1，迪杰斯特拉算法将算出V1到其他所有点的最短路径，则所求V1到终点的最短路径也可得到，该算法主要完成以下几步：

1. 找到V1
2. 得到以V1出发的邻接点的最短距离，将V1加到S集合中（代码中通过vis数组标记）
3. 从S集合之外的点中找到距离最短者，对以其为出发点的邻接点进行松弛操作，若距离被更新，则记录前驱
4. 重复3，直到所有点被S集合收录
5. 完成后，将得到V1到所有点的最短距离，同时，通过每一个点记录的前驱得到最短路径

1.1 问题：

1. 松弛操作是啥？

松弛操作意味着比起原来的路径，找到了一条距离更短的路，则将原来点的距离更新为新的距离。注意本文中某个点的距离全部指的是从出发点即V1到该点的距离。代码如下：

 if(dis[j]>dis[k]+map[k][j])
 {
      dis[j]=dis[k]+map[k][j];
      path[j]=k;
 }

2. 为啥每个点记录前驱能用于V1到所有终点？

我的理解是最短路是由最短路+某一条固定路组成，所以前驱适用全部点，比如该图中V1到V7的最短路径为V1->V2->V3->V5->V6->V7，因为V6->V7的距离固定为50，所以V7的最短路径中V1->V6的一段必然是V1->V6的最短路径，因此每个结点只需记录一个前驱。要想打印出路径，从终点开始一次次找前驱即可，可通过递归实现。代码如下：

void print(int x)//x为终点
{
    if(x == -1) return;
    //递归
    print(path[x]);
    printf("%d->",x);
}

1.2 算法过程

程序运行过程中，数据的更新情况如图所示：

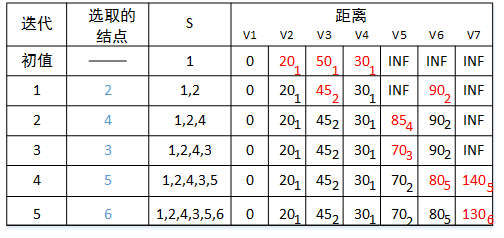
画这个破图累死了，红色数据代表每次迭代中被更新的数据，下标代表了结点前驱。由上图可得，当所有结点加入S后，就得到了V1到所有结点的最短距离和最短路径，例如V1到V7的最短距离为130，V7的前驱为V6，V6的前驱为V5，V5的前驱为V3，V3的前驱为V2，V2的前驱为V1，则V1到V7的最短路径为V1->V2->V3->V5->V6->V7。

2 代码详解

以下为上述实例的完整代码，代码中详细注释了该算法中关键操作以及容易被误解的地方。

#include <iostream>
#include <cstring>
#include <cstdio>

/*问题描述：
 * 输入n和m，代表n个节点，m条边，然后是m行输入，每行有x,y,z，代表x到y的路距离为z。
 * 问题：从1出发到各点的最短路径。
 * 测试样例：
7 12
1 2 20
1 3 50
1 4 30
2 3 25
2 6 70
3 4 40
3 6 50
3 5 25
4 5 55
5 6 10
5 7 70
6 7 50
 */
using namespace std;
const int maxn = 100;
int map[maxn][maxn];
int dis[maxn];
int path[maxn];
int vis[maxn];//记录更新过的点
int n;
void dijk(int s)
{
    //初始化
    memset(path,-1,sizeof(path));
    /*INF使用0x3f3f3f3f的好处：
     * 1：满足无穷大加一个有穷的数依然是无穷大（在DijKstra算法松弛操作中避免了溢出而出现负数）
     * 2：满足无穷大加无穷大依然是无穷大（两个0x3f3f3f3f相加并未溢出）
     * 3：初始化时，由于每一个字节为0x3f，所以只需要memset（buf，0x3f,sizeof(buf)）即可
     */
    memset(dis,0x3f,sizeof(dis)); //初始化为无穷大
    memset(vis,0,sizeof(vis));
    dis[s] = 0; //自身到自身的距离为0
    while(1)
    {
        int k = 0;
        for(int j = 1; j <= n; j++)
        {
            if(!vis[j]&&dis[j]<dis[k])//找未收录顶点中dis值最小的
                k=j; //这里第一次找到的是起点
        }
        if(!k) return; //没有未收录的点，则返回
        vis[k] = 1;
        //松弛操作
        for(int j = 1; j <= n; j++)
        {
            //第一次循环只有起点的邻接点距离被更新，每次都更新新找到的点的邻接点
            if(dis[j]>dis[k]+map[k][j])
            {
                dis[j]=dis[k]+map[k][j];
                path[j]=k;//路径被改变，重新记录前驱，最短路是由最短路+某一条固定路组成，所以前驱是有效的
            }
        }
    }
}

void print(int x)//x为终点
{
    if(x == -1) return;
    //递归
    print(path[x]);
    printf("%d->",x);
}
int main()
{
    int m,x,y,z,order;
    scanf("%d%d",&n,&m);
    memset(map,0x3f,sizeof(map));
    for(int i = 0; i < m; i++)
    {
        scanf("%d%d%d",&x,&y,&z);
        map[x][y] = z;
    }
    dijk(1);
    scanf("%d",&order);//order为终点
    print(path[order]);
    printf("%d\n",order);
    //打印最短距离
    printf("%d\n",dis[order]);
    return 0;
}

代码之所以能这么写，是因为初始化的时候置不连通的点之间的距离为INF，在寻找最短路径估计最小的结点u以及在是否松弛的判断中这点至关重要，请读者细细体会。

补充：基于堆优化的dijkstra算法代码 可以把时间复杂度从O(v^2)降到O(elogv)。

#include 
using namespace std;

const int MAXN = 1e2 + 5;

//基于堆优化的dijkstra算法
struct edge{
    int to;//终点
    int cost;//权重
    edge(int x, int y):to(x), cost(y){}
};
typedef pair<int, int> P;//first是最短距离 second是顶点的编号
vector<edge> graph[MAXN];//邻接表
int dist[MAXN];//距离
int path[MAXN];//记录前驱
void dijkstra(int s){
    //初始化前驱
    memset(path,-1,sizeof(path));
    //默认对pair.first的大小进行排序 从小到大
    priority_queue<P, vector<P>, greater<P>> que;
    //初始化距离
    memset(dist, 0x3f, sizeof(dist));
    dist[s] = 0;
    que.push(P(0,s));//把起点压入队列
    while(!que.empty()){
        P p = que.top();
        que.pop();
        //顶点的编号
        int v = p.second;
        //dist[v]经过松弛操作变小，压入堆中的路径失去价值
        if(dist[v] < p.first) continue;
        //利用最短边进行松弛
        for(int i= 0; i < graph[v].size(); ++i){
            edge e = graph[v][i];
            if(dist[e.to] > dist[v] + e.cost){
                dist[e.to] = dist[v] + e.cost;
                que.push(P(dist[e.to],e.to));
                path[e.to] = v;
            }
        }
    }
}
//打印路径
void print(int x)//x为终点
{
    if(x == -1) return;
    //递归
    print(path[x]);
    printf("%d->",x);
}
int main()
{
    //读入数据
    int m, n, x, y, z;
    int order;
    scanf("%d%d", &n, &m);
    for(int i = 0; i < m; ++i){
        scanf("%d%d%d",&x,&y,&z);
        graph[x].push_back(edge(y, z));
    }
    dijkstra(1);
    scanf("%d",&order);//order为终点
    print(path[order]);
    printf("%d\n",order);
    //打印最短距离
    printf("%d\n",dist[order]);
    return 0;
}