ACM: 百练NOI——基本算法之动态规划
文章目录
- Maximum sum(求两个不重叠子区间最大和)
- Post Office(感觉题解有问题)
- 最长上升子序列
- 最大子矩阵
- 采药(0-1背包)
- 最长公共子序列
- 吃糖果
- 登山
- 最长公共上升子序列**(记录路径)
- Exchange Rates
- 移动路线
- 摘花生
- 数字组合
- 糖果(模k 0-1背包)
- 判断整除(模k 0-1背包)
- 最大上升子序列
- 怪盗基德的滑翔伞
- 宠物小精灵之收服(二维背包)
- 采方格
- 开餐馆
- 买书
- 带通配符的字符串匹配
- 放苹果
- 最低通行费
- 三角形的最佳路径
- 鸡蛋的硬度
- 大盗阿福
- 切割回文
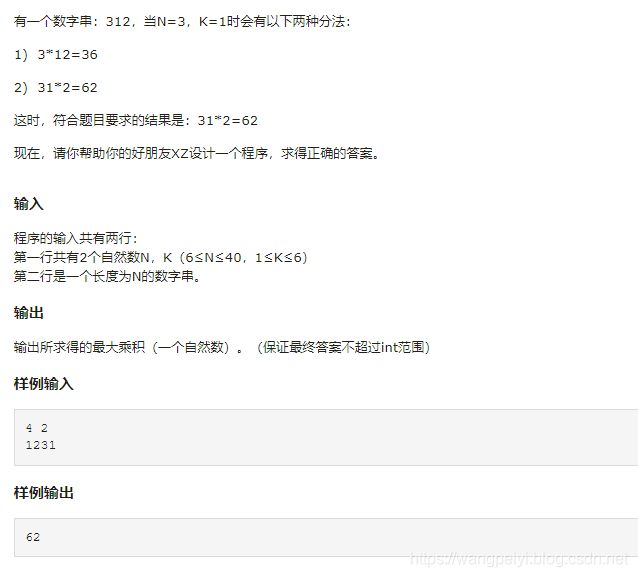
- 乘积最大
- 装箱问题
- 方格取数
- 滑雪
- 核电站问题
- 酒鬼
- Pku2440 DNA
- 奶牛散步
- [Usaco2009 Feb]Bullcow
- Logs Stacking堆木头
Maximum sum(求两个不重叠子区间最大和)
一、题目大意:
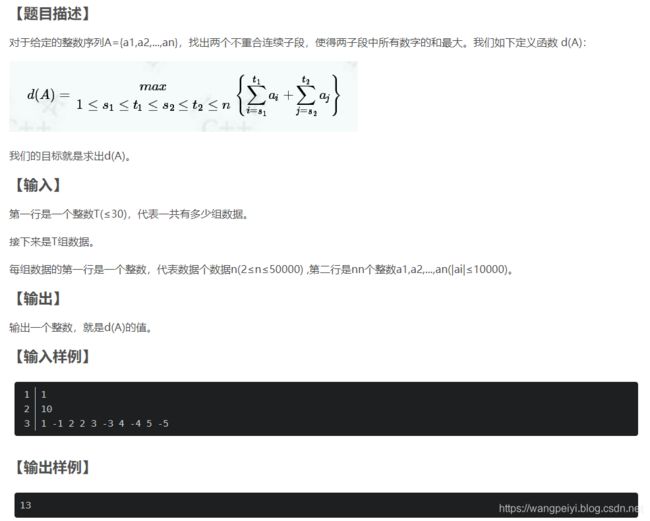
二、解题思路:
(1): 所求的两个子序列必定以一个数为分割点。
(2): 左边的子序列必定以分割点或者左边的其中一个数为结尾,右边的子序列必定以分割点右边的其中一个数为起始。
- 定义状态:
- q i a n [ i ] qian[i] qian[i]: 以 a [ i ] a[i] a[i]为结尾的最大连续子序列和。
- h o u [ i ] hou[i] hou[i]: 以 a [ i ] a[i] a[i]为起始的最大连续子序列和。
- t o t a l 1 [ i ] total1[i] total1[i]: [ 0 , i ] [0,i] [0,i]区间内的最大连续子序列和。
- t o t a l 2 [ i ] total2[i] total2[i]: [ i , n − 1 ] [i,n-1] [i,n−1]区间内的最大连续子序列和。
- 目标状态: m a x ( { t o t a l 1 [ i ] + t o t a l 2 [ i + 1 ] ∣ 0 < = i < n } ) max(\{total1[i]+total2[i+1]\quad | \quad 0<=i<n\}) max({total1[i]+total2[i+1]∣0<=i<n})
- 状态转移:
- q i a n [ i ] = m a x ( a [ i ] , q i a n [ i − 1 ] + a [ i ] ) qian[i] = max(a[i],qian[i-1]+a[i]) qian[i]=max(a[i],qian[i−1]+a[i])
- h o u [ i ] = m a x ( a [ i ] , h o u [ i + 1 ] + a [ i ] ) hou[i] = max(a[i], hou[i+1]+a[i]) hou[i]=max(a[i],hou[i+1]+a[i])
- t o t a l 1 [ i ] = m a x ( { q i a n [ k ] ∣ 0 < = k < = i } ) total1[i] = max(\{qian[k]\quad|\quad 0<=k<=i\}) total1[i]=max({qian[k]∣0<=k<=i})
- t o t a l 2 [ i ] = m a x ( { h o u [ k ] ∣ i < = k < = n − 1 } ) total2[i] = max(\{hou[k]\quad|\quad i<=k<=n-1\}) total2[i]=max({hou[k]∣i<=k<=n−1})
- 初始状态:
- q i a n [ 0 ] = a [ 0 ] qian[0] = a[0] qian[0]=a[0],
- h o u [ n − 1 ] = a [ n − 1 ] hou[n-1] = a[n-1] hou[n−1]=a[n−1]
- 复杂度: O ( n ) O(n) O(n)
三、代码:
#include
using namespace std;
const int MAX = 50000+5;
const int inf = 1 << 29;
int T;
int main()
{
int qian[MAX], hou[MAX], total1[MAX], total2[MAX];
int a[MAX];
cin >> T;
for(int i=0; i> n;
for(int j=0; j> a[j];
qian[0] = a[0];
for(int j=1; j=0; j--)
hou[j] = max(a[j], hou[j+1]+a[j]);
total1[0] = qian[0];
for(int j=1; j=0; j--)
total2[j] = max(total2[j+1], hou[j]);
int ans = -inf;
for(int j=0; j Post Office(感觉题解有问题)
- 定义:
- d p [ i ] [ j ] dp[i][j] dp[i][j]:前 i i i个村庄建 j j j个邮局的最小距离.
- m [ i ] [ j ] m[i][j] m[i][j]:村庄 [ i , j ] [i,j] [i,j]之间建立一个邮局的最小距离.(想象: 很明显应该建在 ( i + j ) / 2 (i+j)/2 (i+j)/2的邮局上)
- 目标状态: d p [ V ] [ P ] dp[V][P] dp[V][P].即前 V V V个村庄建立 P P P个邮局.
- 状态转移:
- 子问题:
- 定义: b u i l d ( s , e , j ) : = build(s,e,j):= build(s,e,j):=在村庄 [ s , e ] [s,e] [s,e] 间建 j j j个邮局
- b u i l d ( 1 , i , j ) : = ⋃ k = 1 i − 1 { b u i l d ( 1 , k , j − 1 ) ∩ b u i l d ( k + 1 , i , 1 ) } build(1,i,j):=\bigcup_{k=1}^{i-1} \{build(1,k , j-1)\cap build(k+1, i, 1)\} build(1,i,j):=⋃k=1i−1{build(1,k,j−1)∩build(k+1,i,1)}
- 因此有: 状态转移方程: d p [ i ] [ j ] = m a x { d p [ k ] [ j − 1 ] + m [ k + 1 ] [ i ] ∣ 1 < = k < = i − 1 } dp[i][j] = max\{dp[k][j-1]+m[k+1][i]\quad | \quad 1<=k<=i-1\} dp[i][j]=max{dp[k][j−1]+m[k+1][i]∣1<=k<=i−1}(这里默认了每一个子问题下,最优情况为: 前 k k k个村庄只往前 j − 1 j-1 j−1个邮局前进,如果是要往第 j j j个邮局,这种情况包含在其他子问题下)因此状态转移最终结果没有问题。
- m [ i ] [ j ] = m [ i ] [ j − 1 ] + a [ j ] − a [ ( i + j ) / 2 ] m[i][j] = m[i][j-1]+a[j]-a[(i+j)/2] m[i][j]=m[i][j−1]+a[j]−a[(i+j)/2](想象可得出)
- 子问题:
- 转移策略: 先求出所有的 m m m, d p [ i ] [ j ] dp[i][j] dp[i][j]只依赖与 d p [ i ′ ] [ j − 1 ] dp[i'][j-1] dp[i′][j−1],因此只需循环更新下三角矩阵。
- 初始状态: d p [ i ] [ 1 ] = m [ 1 ] [ i ] , d p [ i ] [ 0 ] = i n f dp[i][1] = m[1][i], dp[i][0]=inf dp[i][1]=m[1][i],dp[i][0]=inf
三、 代码:
#include
using namespace std;
const int MAXV = 304;
const int MAXP = 34;
const int inf = 1 << 30;
int dp[MAXV][MAXP];
int m[MAXV][MAXV];
int a[MAXV];
int main()
{
int V, P;
cin >> V >> P;
for(int i=1; i<=V; i++)
cin >> a[i];
for(int i=0; i<=V; i++)
for(int j=0; j<=P; j++)
dp[i][j] = inf;
for(int i=1; i<=V; i++)
m[i][i] = 0;
for(int i=1; i<=V; i++)
for(int j=i+1; j<=V; j++)
m[i][j] = m[i][j-1] + a[j] - a[(i+j)/2];
for(int i=1; i<=V; i++)
dp[i][1] = m[1][i];
for(int i=2; i<=V; i++)
for(int j=1; j<=i; j++)
for(int k=1; k<=i-1; k++)
dp[i][j] = min(dp[i][j], dp[k][j-1]+m[k+1][i]);
cout << dp[V][P] << endl;
return 0;
}
最长上升子序列
会议状态转移、初态。题解略, 代码
#include
using namespace std;
const int MAXN = 1005;
int a[MAXN];
int main()
{
int n;
cin >> n;
for(int i=1; i<=n; i++)
cin >> a[i];
int dp[MAXN];
dp[1] = 1;
for(int i=2; i<=n; i++)
{
dp[i] = 1;
for(int j=1; j<=i-1; j++)
{
if(a[i] > a[j])
dp[i] = max(dp[i], dp[j]+1);
}
}
int ans = 0;
for(int i=1; i<=n; i++)
ans = max(ans, dp[i]);
cout << ans << endl;
return 0;
}
最大子矩阵
一、题目大意

二、解题思想
1、利用sum[i][j]记录(i,j)左上方所有的和,然后利用前缀和的思想快速求出某个矩阵的和。最后使用四重循环,但是超时。
2、使用压缩维度和动态规划思想。
(1)压缩维度
- 定义 s u m O f L i n e [ i ] [ j ] sumOfLine[i][j] sumOfLine[i][j]:为第 j j j列上前 i i i行所有数的和。使用 O ( n 2 ) O(n^2) O(n2)求出结果。
(2)动态规划:对任意一个横跨 [ i , j ] [i,j] [i,j]行的矩阵,我们使用 s u m O f L i n e sumOfLine sumOfLine快速将其压缩为一维,然后求这个一维数组的最大连续子序列和。任意两行组合的最大值即为最终答案。 O ( n 3 ) O(n^3) O(n3)
三、代码
#include
#include
using namespace std;
const int MAX = 105;
const int inf = 1 << 30;
int grad[MAX][MAX];
int sum_of_line[MAX][MAX];
int line[MAX];
int get_max_sequence(int n)
{
int dp[MAX];
dp[1] = line[1];
for(int i=2; i<=n; i++)
dp[i] = max(line[i], dp[i-1]+line[i]);
int res = -inf;
for(int i=1; i<=n; i++)
res = max(dp[i], res);
return res;
}
int main()
{
int n;
scanf("%d", &n);
for(int i=1; i<=n; i++)
for(int j=1; j<=n; j++)
scanf("%d", &grad[i][j]);
// ---------------计算行前缀和-----------------------------
for(int j=1; j<=n; j++)
for(int i=1; i<=n; i++)
sum_of_line[i][j] = sum_of_line[i-1][j] + grad[i][j];
// --------------------------------------------------------------
int ans = -inf;
for(int r1=1; r1<=n; r1++)
{
for(int r2=r1; r2<=n; r2++)
{
for(int j=1; j<=n; j++)
line[j] = sum_of_line[r2][j] - sum_of_line[r1-1][j];
int line_max = get_max_sequence(n);
ans = max(line_max, ans);
}
}
cout << ans << endl;
return 0;
}
采药(0-1背包)
#include
using namespace std;
const int MAXT = 1005;
const int MAXN = 105;
int dp[2][MAXT];
int time[MAXN];
int value[MAXN];
int max(int a, int b)
{
if(a < b)
return b;
return a;
}
int main()
{
int T, M;
scanf("%d%d", &T, &M);
for(int i=1; i<=M; i++)
scanf("%d%d", &time[i], &value[i]);
for(int i=0; i<=T; i++)
dp[0][i] = 0;
for(int i=1; i<=M; i++)
{
for(int j=1; j<=T; j++)
{
if(j-time[i] >= 0)
dp[i%2][j] = max(dp[1-i%2][j], dp[1-i%2][j-time[i]] + value[i]);
else
dp[i%2][j] = dp[1-i%2][j];
}
}
printf("%d\n", dp[M%2][T]);
return 0;
}
最长公共子序列
基本dp,回忆状态转移,代码:
#include
using namespace std;
const int MAX = 205;
int dp[MAX][MAX];
int main()
{
string s1, s2;
while(cin >>s1 >> s2)
{
int l1 = s1.length();
int l2 = s2.length();
for(int i=0; i<=max(l1, l2); i++)
{
dp[0][i] = 0;
dp[i][0] = 0;
}
for(int i=1; i<=l1; i++)
{
for(int j=1; j<=l2; j++)
{
if(s1[i-1] == s2[j-1])
dp[i][j] = dp[i-1][j-1] + 1;
else
dp[i][j] = max(dp[i-1][j], dp[i][j-1]);
}
}
cout << dp[l1][l2] << endl;
}
return 0;
}
吃糖果
定义: d p [ i ] dp[i] dp[i],还剩 i i i块的吃法
代码:
#include
using namespace std;
typedef long long ll;
ll dp[25];
int main()
{
dp[1] = 1;
dp[2] = 2;
int N;
cin >> N;
for(int i=3; i<=N; i++)
dp[i] = dp[i-1]+dp[i-2];
cout << dp[N] << endl;
return 0;
}
登山
一、题目大意
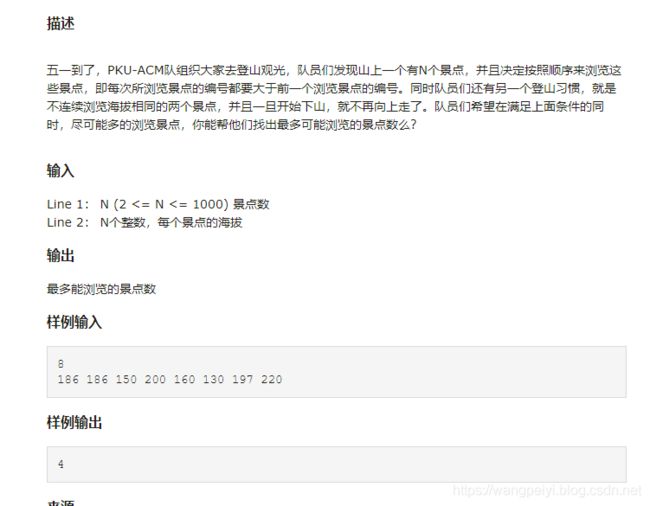
二、解题思想:
最优路线肯定以其中一个点为峰值点,因此求从左到右和从右到左的最长上升子序列
三、代码:
#include
using namespace std;
const int MAXN = 1005;
int dp1[MAXN];
int dp2[MAXN];
int main()
{
int n;
cin >> n;
int a[MAXN];
for(int i=1; i<=n; i++)
cin >> a[i];
dp1[1] = 1;
for(int i=2; i<=n; i++)
{
dp1[i] = 1;
for(int j=1; j=0; i--)
{
dp2[i] = 1;
for(int j=n; j>i; j--)
{
if(a[i] > a[j])
dp2[i] = max(dp2[i], dp2[j] + 1);
}
}
int ans = -1;
for(int i=1; i<=n; i++)
ans = max(ans, dp1[i] + dp2[i] - 1);
cout << ans << endl;
return 0;
}
最长公共上升子序列**(记录路径)
Exchange Rates
一、题目大意
有两种货币US / Canada Dollor, 每天给出两种货币的汇率,然后可以选择全部换或者不换,换的时候要缴纳0.03的手续费(换之后),并且两位小数后的钱直接不要,刚开始时有1000 Canada Dollor,问给出N天的Canada Dollor对US Dollor的汇率,最后第N天最多可以有多少Canada Dollor。
二、解题思路
- 定义状态 d p [ i ] [ k ] , k ∈ { 0 , 1 } dp[i][k], k\in\{0,1\} dp[i][k],k∈{0,1}:当 k = 1 k=1 k=1时,为第 i i i天最多可拥有的
us dollor, k = 0 k=0 k=0为第 i i i天最多可拥有的can dollor. - 目标状态: d p [ N ] [ 0 ] dp[N][0] dp[N][0]
- 状态转移方程: d p [ i ] [ 0 ] = m a x ( d p [ i − 1 ] [ 0 ] , d p [ i − 1 ] [ 1 ] ∗ a [ i ] ∗ 0.97 ) dp[i][0]=max(dp[i-1][0], dp[i-1][1]*a[i]*0.97) dp[i][0]=max(dp[i−1][0],dp[i−1][1]∗a[i]∗0.97) d p [ i ] [ 1 ] = m a x ( d p [ i − 1 ] [ 1 ] , d p [ i − 1 ] [ 0 ] / a [ i ] ∗ 0.97 ) dp[i][1] = max(dp[i-1][1], dp[i-1][0]/a[i]*0.97) dp[i][1]=max(dp[i−1][1],dp[i−1][0]/a[i]∗0.97)
- 初态: d p [ 0 ] [ 0 ] = 1000 , d p [ 0 ] [ 1 ] = 0 dp[0][0] = 1000, dp[0][1]=0 dp[0][0]=1000,dp[0][1]=0
三、代码
#include
#include
#include
using namespace std;
const int MAXD = 366;
double dp[MAXD][2];
double a[MAXD];
int N;
double remove_cent(double x)
{
return floor(x * 100)*1.0 / 100;
}
int main()
{
while(cin >> N && N)
{
for(int i=1; i<=N; i++)
cin >> a[i]; // 指a[i] Canada dollor <----> 1 US dollor, 即换出的时候应该越小越好,换进的时候越大越好
dp[0][0] = 1000;
dp[0][1] = 0;
for(int i=1; i<=N; i++)
{
dp[i][0] = max(dp[i-1][0], remove_cent(dp[i-1][1]*a[i]*0.97));
dp[i][1] = max(dp[i-1][1], remove_cent(dp[i-1][0]/a[i]*0.97));
}
// cout << dp[N][0] << endl;
printf("%.2lf\n",dp[N][0]);
}
return 0;
}
移动路线
- 定义 d p [ i ] [ j ] : dp[i][j]: dp[i][j]:从第 ( i , j ) (i,j) (i,j)个格子到终点的路线数量。
- 目标状态 d p [ 1 ] [ 1 ] dp[1][1] dp[1][1]:即从起点出发的路线数量。
- 状态转移方程: d p [ i ] [ j ] = d p [ i + 1 ] [ j ] + d p [ i ] [ j + 1 ] dp[i][j] = dp[i+1][j]+dp[i][j+1] dp[i][j]=dp[i+1][j]+dp[i][j+1]
- 初态 d p [ m ] [ n ] = 1 , d p [ 0 ] [ ∗ ] = d p [ ∗ ] [ 0 ] = 0 dp[m][n]=1, dp[0][*]=dp[*][0]=0 dp[m][n]=1,dp[0][∗]=dp[∗][0]=0
- 更新方式,采用记忆化搜索方便写代码
三、代码
#include
#include
using namespace std;
typedef long long ll;
ll dp[25][25];
int get_num(int x, int y)
{
if(dp[x][y] >= 0)
return dp[x][y];
dp[x][y] = get_num(x+1, y) + get_num(x, y+1);
return dp[x][y];
}
int main()
{
int n, m;
cin >> n >> m;
memset(dp, -1, sizeof(dp));
for(int i=0; i<25; i++)
dp[n+1][i] = dp[i][m+1] = 0;
dp[n][m] = 1;
cout << get_num(1,1) << endl;
return 0;
}
摘花生
- 定义: d p [ i ] [ j ] : dp[i][j]: dp[i][j]:从 ( i , j ) (i,j) (i,j)出发到终点过程中最多还能采摘的花生数。
- 目标: d p [ 1 ] [ 1 ] dp[1][1] dp[1][1]
- 状态转移: d p [ i ] [ j ] = g r a d [ i ] [ j ] + m a x ( d p [ i + 1 ] [ j ] , d p [ i ] [ j + 1 ] ) dp[i][j] = grad[i][j]+max(dp[i+1][j], dp[i][j+1]) dp[i][j]=grad[i][j]+max(dp[i+1][j],dp[i][j+1])
- 初态: d p [ c ] [ r ] = 1 , d p [ c + 1 ] [ ∗ ] = d p [ ∗ ] [ r + 1 ] = 0 dp[c][r]=1, dp[c+1][*] = dp[*][r+1] = 0 dp[c][r]=1,dp[c+1][∗]=dp[∗][r+1]=0
- 更新方式,采用记忆化搜索。
三、代码
#include
#include
using namespace std;
const int MAXM = 105;
typedef long long ll;
ll dp[MAXM][MAXM];
int grad[MAXM][MAXM];
ll get_num(int x, int y)
{
if(dp[x][y] >= 0)
return dp[x][y];
dp[x][y] = grad[x][y] + max(get_num(x+1, y), get_num(x, y+1));
return dp[x][y];
}
int main()
{
int r, c;
int T;
cin >> T;
while(T--)
{
cin >> r >> c;
for(int i=1;i<=r; i++)
{
for(int j=1; j<=c; j++)
{
cin >> grad[i][j];
}
}
memset(dp, -1, sizeof(dp));
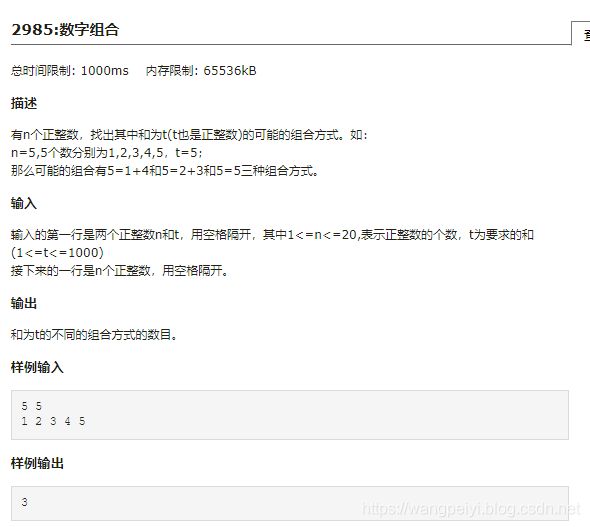
for(int i=0; i 数字组合
- 定义 d p [ i ] [ j ] dp[i][j] dp[i][j]:前 i i i个数组成 j j j的方式数量。
- 目标 d p [ n ] [ t ] dp[n][t] dp[n][t].
- 状态转移: d p [ i ] [ j ] = { d p [ i − 1 ] [ j ] + d p [ i − 1 ] [ j − a [ i ] ] j − a [ i ] > = 0 d p [ i − 1 ] [ j ] e l s e dp[i][j] = \begin{cases} dp[i-1][j] + dp[i-1][j-a[i]]& j - a[i]>=0\\ dp[i-1][j] & else \end{cases} dp[i][j]={dp[i−1][j]+dp[i−1][j−a[i]]dp[i−1][j]j−a[i]>=0else
初始状态: d p [ 0 ] [ ∗ ] = 0 , d p [ 0 ] [ 0 ] = 1 dp[0][*] = 0, dp[0][0]=1 dp[0][∗]=0,dp[0][0]=1
三、代码
#include
#include
using namespace std;
const int MAXN = 25;
const int MAXT = 1005;
typedef long long ll;
ll dp[MAXN][MAXT];
int a[MAXN];
int main()
{
int n, t;
cin >> n >> t;
for(int i=1; i<=n; i++)
cin >> a[i];
for(int i=0; i<=t; i++)
dp[0][i] = 0;
dp[0][0] = 1;
for(int i=1; i<=n; i++)
{
for(int j=0; j<=t; j++)
{
if(j-a[i] >= 0)
{
dp[i][j] = dp[i-1][j] + dp[i-1][j-a[i]];
}
else
dp[i][j] = dp[i-1][j];
}
}
cout << dp[n][t] << endl;
return 0;
}
糖果(模k 0-1背包)
一、题目大意
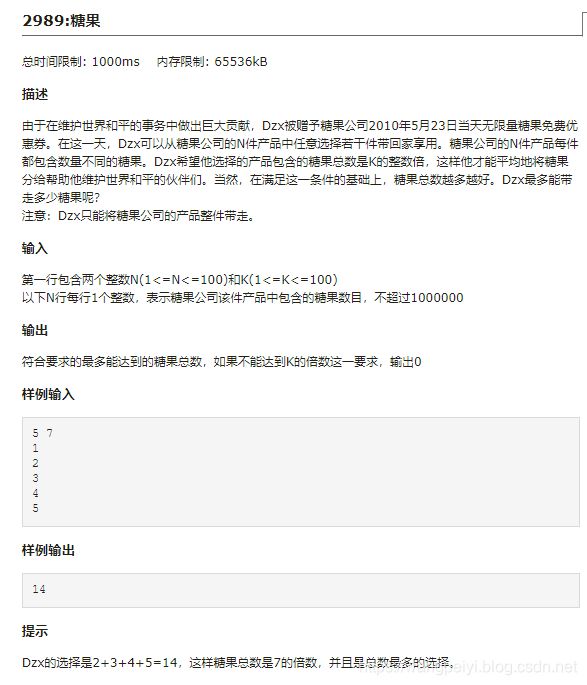
二、解题思想
这里的 T T T实在太大了,如果直接用0-1背包,会超时,这类题给出了倍数的概念,那么就要往取模上考虑了。
- 定义 d p [ i ] [ j ] : dp[i][j]: dp[i][j]:前 i i i个物品中选择物品使得重量和
模k等于 j j j的最大重量。 - 目标状态 d p [ n ] [ 0 ] dp[n][0] dp[n][0].
- 状态转移:
- 子问题: 对第 i i i个物品来说,依然有选或者不选两种选择。
- 不选:很明显 d p [ i ] [ j ] = d p [ i − 1 ] [ j ] dp[i][j] = dp[i-1][j] dp[i][j]=dp[i−1][j]
- 选: d p [ i ] [ j ] = d p [ i − 1 ] [ ( ( j − a [ i ] ) % k + k ) % k ] + a [ i ] dp[i][j] = dp[i-1][((j-a[i])\%k+k)\%k] + a[i] dp[i][j]=dp[i−1][((j−a[i])%k+k)%k]+a[i]
- 状态转移方程:
d p [ i ] [ j ] = m a x ( d p [ i − 1 ] [ j ] , d p [ i − 1 ] [ ( ( j − a [ i ] ) % k + k ) % k ] + a [ i ] ) dp[i][j] = max(dp[i-1][j], dp[i-1][((j-a[i])\%k+k)\%k]+a[i]) dp[i][j]=max(dp[i−1][j],dp[i−1][((j−a[i])%k+k)%k]+a[i])
- 子问题: 对第 i i i个物品来说,依然有选或者不选两种选择。
- 初态: d p [ 0 ] [ ∗ ] = − i n f , d p [ 0 ] [ 0 ] = 0 dp[0][*]=-inf, dp[0][0]=0 dp[0][∗]=−inf,dp[0][0]=0
三、代码
#include
using namespace std;
const int MAXM = 100+5;
const int inf = 1<<30;
typedef long long ll;
ll dp[MAXM][MAXM];
ll a[MAXM];
int main()
{
int n,k;
cin >> n >> k;
for(int i=1;i<=n; i++)
cin >> a[i];
for(int i=0; i 判断整除(模k 0-1背包)
- 定义: d p [ i ] [ j ] ∈ { 0 , 1 } : dp[i][j]\in\{0,1\}: dp[i][j]∈{0,1}:前 i i i个数组合模 k k k是否能够等于 j j j.
- 目标状态: d p [ n ] [ 0 ] dp[n][0] dp[n][0]
- 状态转移:
d p [ i ] [ j ] = d p [ i − 1 ] [ ( j + a [ i ] ) % k ] ∣ d p [ i − 1 ] [ ( ( j − a [ i ] ) % k + k ) ] dp[i][j] = dp[i-1][(j+a[i])\%k]\quad|\quad dp[i-1][((j-a[i])\%k+k)] dp[i][j]=dp[i−1][(j+a[i])%k]∣dp[i−1][((j−a[i])%k+k)]. - 初态: d p [ 0 ] [ ∗ ] = 0 , d p [ 0 ] [ 0 ] = 1 dp[0][*]=0, dp[0][0]=1 dp[0][∗]=0,dp[0][0]=1
三、代码
#include
#include
using namespace std;
const int MAXN = 10005;
const int MAXK = 105;
int dp[MAXN][MAXK]; // dp[i][j]:前i个数模k是否能够等于j
int a[MAXN];
int main()
{
int n, k;
cin >> n >> k;
for(int i=1; i<=n; i++)
cin >> a[i];
for(int i=0; i 最大上升子序列
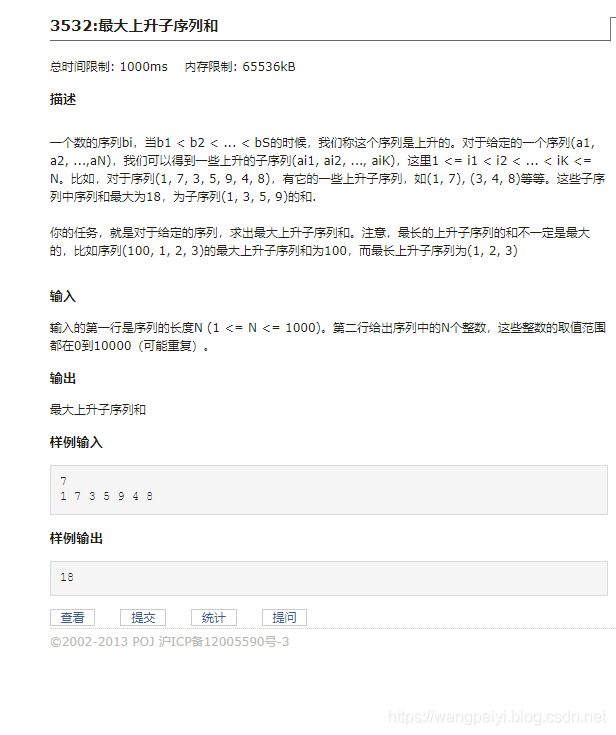
- 定义 d p [ i ] dp[i] dp[i]:以 a [ i ] a[i] a[i]为结尾的最大子序列和。
- 目标态: m a x { d p [ k ] ∣ 1 < = k < = n } max\{dp[k]\quad | \quad 1<=k<=n\} max{dp[k]∣1<=k<=n}
- 状态转移方程: d p [ i ] = m a x ( a [ i ] , { d p [ j ] + a [ i ] ∣ j < i & a [ j ] < a [ i ] } ) dp[i] = max(a[i], \{dp[j]+a[i]\quad | \quad j<i \&a[j]<a[i]\}) dp[i]=max(a[i],{dp[j]+a[i]∣j<i&a[j]<a[i]})
- 初态: d p [ 1 ] = a [ 1 ] dp[1] = a[1] dp[1]=a[1]
三、代码
#include
using namespace std;
const int MAXN = 1005;
int dp[MAXN];
int a[MAXN];
int main()
{
int n;
cin >> n;
for(int i=1; i<=n; i++)
cin >> a[i];
dp[1] = a[1];
for(int i=2; i<=n; i++)
{
dp[i] = a[i];
for(int j=1; j 怪盗基德的滑翔伞
一、题目大意
直接见题目
二、解题思路
(1)开始时必在一栋建筑物上。
(2)可以选择往左往右。
因此是求往左和往右的两个最长上升子序列。
三、代码
#include
using namespace std;
const int MAXN = 105;
int dp1[MAXN];
int dp2[MAXN];
int a[MAXN];
int main()
{
int T;
cin >> T;
while(T--)
{
int n;
cin >> n;
for(int i=1; i<=n; i++)
cin >> a[i];
dp1[1] = 1;
for(int i=2; i<=n; i++)
{
dp1[i] = 1;
for(int j=1; j=1; i--)
{
dp2[i] = 1;
for(int j=n; j>i; j--)
{
if(a[i] > a[j])
dp2[i] = max(dp2[j]+1, dp2[i]);
}
}
int ans = 0;
for(int i=1; i<=n; i++)
ans = max(ans, max(dp1[i], dp2[i]));
cout << ans << endl;
}
return 0;
}
宠物小精灵之收服(二维背包)
一、题目大意
这里
二、解题思路
这是一个二维背包问题。
- 定义 d p [ i ] [ j ] [ k ] dp[i][j][k] dp[i][j][k]: 前 i i i个宠物中,有 j j j个球,皮卡丘体力为 k k k的情况下最多收服的数量。
- 终态 a r g m i n k { d p [ N ] [ Q ] [ k ] = d p [ N ] [ Q ] [ T ] } argmin_{k} \quad \{dp[N][Q][k] = dp[N][Q][T]\} argmink{dp[N][Q][k]=dp[N][Q][T]}
- 状态转移: d p [ i ] [ j ] [ k ] = { m a x ( d p [ i − 1 ] [ j ] [ k ] , d p [ i − 1 ] [ j − q i u [ i ] ] [ k − t [ i ] ] + 1 ) j > = q i u [ i ] , k > = t i [ i ] d p [ i − 1 ] [ j ] [ k ] dp[i][j][k] = \begin{cases} max(dp[i-1][j][k], dp[i-1][j-qiu[i]][k-t[i]] +1)& j>=qiu[i], k>=ti[i]\\ dp[i-1][j][k] \end{cases} dp[i][j][k]={max(dp[i−1][j][k],dp[i−1][j−qiu[i]][k−t[i]]+1)dp[i−1][j][k]j>=qiu[i],k>=ti[i]
- 初始态: d p [ 0 ] [ ∗ ] [ ∗ ] = 0 dp[0][*][*]=0 dp[0][∗][∗]=0
- 实现的时候需要压缩维度,不然超时,另外有点小问题,题干中提到体力减为0不能收服,但是在实际解题中却不能考虑该条件。
三、代码
#include
#include
#include
using namespace std;
int l,m,n,minn;
int A[105][2];
int f[1005][505];
int main()
{
scanf("%d %d %d",&m,&l,&n);
for(int i=1;i<=n;i++)
{
scanf("%d %d",&A[i][0],&A[i][1]);
}
for(int i=1;i<=n;i++)
{
for(int j=m;j>=A[i][0];j--)
{
for(int k=l;k>=A[i][1];k--)
{
f[j][k]=max(f[j][k],f[j-A[i][0]][k-A[i][1]]+1);
}
}
}
printf("%d ",f[m][l]);
for(int i=0;i<=l;i++)
{
if(f[m][i]==f[m][l])
{
minn=i;
break;
}
}
printf("%d",l-minn);
}
采方格
一、题目大意
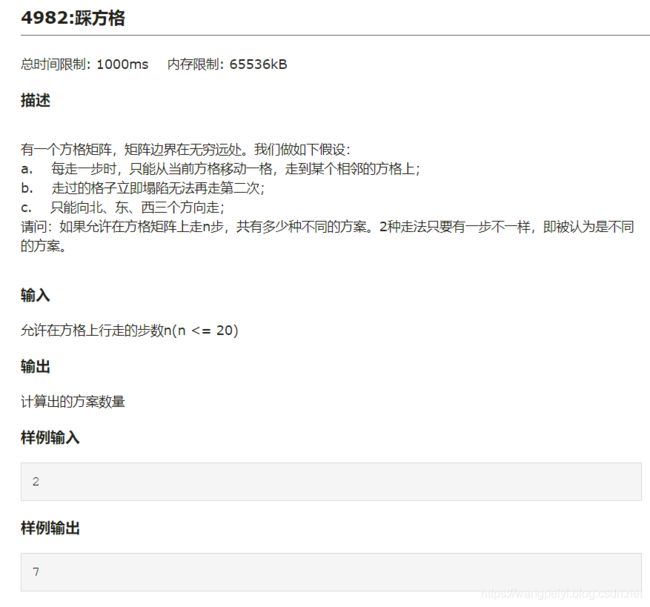
二、解题思路
(1) 搜索法: 由于题中说明了只要任意一步走法不同,就是两种方法,那么基于此我们就能直接进行深搜。
(2) 动态规划: 待思考,可参看博客
三、代码
#include
using namespace std;
int flag[50][50];
int dir[3][2] = {{0,1},{0,-1},{1,0}};
int offset = 20;
int cnt;
void dfs(int x, int y, int t)
{
if(t == 0)
{
cnt++;
return;
}
for(int i=0; i<3; i++)
{
int nx = x + dir[i][0];
int ny = y + dir[i][1];
if(flag[nx][ny]) continue;
flag[nx][ny] = 1;
dfs(nx, ny, t-1);
flag[nx][ny] = 0;
}
return;
}
int main()
{
int n;
cin >> n;
cnt = 0;
flag[0][offset+0] = 1;
dfs(0, 0+offset, n);
cout << cnt << endl;
}
开餐馆
一、题目大意

二、解题思路
(1) 首先肯定会在一个地方开餐馆
(2)如果确定在此开餐馆,就要看两边如何开餐馆利润最大。
- 定义:
- d p 1 [ i ] : dp1[i]: dp1[i]:在 i i i处开餐馆,区间 [ 1 , i ] [1,i] [1,i]开餐馆的最大利润。
- d p 2 [ i ] : dp2[i]: dp2[i]:在 i i i处开餐馆,区间 [ i , n ] [i,n] [i,n]开餐馆的最大利润。
- 目标状态: m a x ( { d p 1 [ i ] + d p 2 [ i ] − p [ i ] ∣ 1 < = i < = n } ) max(\{dp1[i]+dp2[i]-p[i]\quad|\quad 1<=i<=n\}) max({dp1[i]+dp2[i]−p[i]∣1<=i<=n})
- 状态转移: d p 1 [ i ] = m a x ( p [ i ] , { d p 1 [ j ] + p [ i ] ∣ m [ i ] − m [ j ] > k & i > j } dp1[i] = max(p[i],\{dp1[j]+p[i]\quad | \quad m[i]-m[j]>k \& i>j\} dp1[i]=max(p[i],{dp1[j]+p[i]∣m[i]−m[j]>k&i>j}
(要么独自开,要么前面开的最邻近的一家为前面满足条件的地点之一)
d p 2 [ i ] = m a x ( p [ i ] , { d p 2 [ j ] + p [ i ] ∣ m [ j ] − m [ i ] > k & j > i } dp2[i]=max(p[i], \{dp2[j]+p[i] \quad | \quad m[j]-m[i]>k \& j>i\} dp2[i]=max(p[i],{dp2[j]+p[i]∣m[j]−m[i]>k&j>i} - 初态: d p [ 1 ] = p [ 1 ] , d p 2 [ n ] = p [ n ] dp[1]=p[1], dp2[n]=p[n] dp[1]=p[1],dp2[n]=p[n]
三、代码
#include
using namespace std;
const int MAXN = 1005;
int p[MAXN];
int m[MAXN];
int dp1[MAXN];
int dp2[MAXN];
int main()
{
int T;
cin >> T;
while(T--)
{
int n , k;
cin >> n >> k;
for(int i=1; i<=n; i++)
cin >> m[i];
for(int i=1; i<=n; i++)
cin >> p[i];
dp1[1] = p[1];
for(int i=2; i<=n; i++)
{
dp1[i] = p[i];
for(int j=1; j k)
{
dp1[i] = max(dp1[i], dp1[j]+p[i]);
}
}
}
dp2[n] = p[n];
for(int i=n-1; i>=1; i--)
{
dp2[i] = p[i];
for(int j=n; j>i; j--)
{
if(m[j]-m[i] > k)
{
dp2[i] = max(dp2[i], dp2[j]+p[i]);
}
}
}
int ans = 0;
for(int i=1; i<=n; i++)
ans = max(ans, dp1[i]+dp2[i]-p[i]);
cout << ans << endl;
}
return 0;
}
买书
- 定义 d p [ i ] [ j ] : dp[i][j]: dp[i][j]:前 i i i件物品刚好花完 j j j元钱的总的购买方式总数。
- 目标状态 d p [ 4 ] [ n ] dp[4][n] dp[4][n]。
- 状态转移:
d p [ i ] [ j ] = ∑ 0 j / a [ i ] d p [ i − 1 ] [ j − a [ i ] ] dp[i][j] = \sum_0^{j/a[i]}dp[i-1][j-a[i]] dp[i][j]=0∑j/a[i]dp[i−1][j−a[i]]
这是完全背包. - 初态 d p [ 0 ] [ ∗ ] = 0 , d p [ 0 ] [ 0 ] = 1 dp[0][*]=0, dp[0][0]=1 dp[0][∗]=0,dp[0][0]=1
三、代码
#include
using namespace std;
int a[5] = {0, 10, 20, 50, 100};
int dp[1000+5];
int main()
{
int n;
cin >> n;
for(int i=0; i<=n; i++)
dp[i] = 0;
dp[0]=1;
for(int i=1; i<=4; i++)**加粗样式**
for(int j=a[i]; j<=n; j++)
dp[j] += dp[j-a[i]];
if(n==0)
cout << 0 << endl;
else
cout << dp[n] << endl;
}
带通配符的字符串匹配
- 定义 d p [ i ] [ j ] ∈ { 0 , 1 } : dp[i][j] \in \{0,1\}: dp[i][j]∈{0,1}:字符串 s 1 s1 s1的前 i i i位和字符串 s 2 s2 s2的前 j j j位是否能匹配。
- 目标状态: d p [ l 1 ] [ l 2 ] dp[l1][l2] dp[l1][l2],其中 l 1 、 l 2 l1、l2 l1、l2分别位两个字符串长度
- 状态转移:
- 选择:
- (1) 若当前 s 1 [ i ] = s 2 [ j ] ∣ ∣ s 1 [ i ] = ′ ? ′ s1[i] = s2[j] || s1[i]='?' s1[i]=s2[j]∣∣s1[i]=′?′, 则 s 1 [ i ] s1[i] s1[i]和 s 2 [ j ] s2[j] s2[j]需要匹配。
- (2) 若当前 s 1 [ i ] ! = s 2 [ j ] & & s 1 [ i ] ! = ′ ∗ ′ s1[i] != s2[j] \&\&s1[i] != '*' s1[i]!=s2[j]&&s1[i]!=′∗′, 则没办法匹配
- (2) 若当前 s 1 [ i ] ! = s 2 [ j ] & & s 1 [ i ] = = ′ ∗ ′ s1[i]!=s2[j] \&\& s1[i] == '*' s1[i]!=s2[j]&&s1[i]==′∗′, 则可以用星号匹配 [ 0 , j ] [0,j] [0,j]个字符,只要其中一个能够匹配就能匹配。
- 方程式:
d p [ i ] [ j ] = { d p [ i − 1 ] [ j − 1 ] s 1 [ i ] = s 2 [ j ] ∣ ∣ s 1 [ i ] = ′ ? ′ 0 s 1 [ i ] ! = s 2 [ j ] & s 1 [ i ] ! = ′ ∗ ′ ∪ { d p [ i − 1 ] [ k ] } 0 < = k < = j dp[i][j] = \begin{cases} dp[i-1][j-1] & s1[i]=s2[j]\quad||\quad s1[i]='?' \\ 0 & s1[i] !=s2[j] \& s1[i] !='*' \\ \cup\{dp[i-1][k]\} & 0<=k <=j \end{cases} dp[i][j]=⎩⎪⎨⎪⎧dp[i−1][j−1]0∪{dp[i−1][k]}s1[i]=s2[j]∣∣s1[i]=′?′s1[i]!=s2[j]&s1[i]!=′∗′0<=k<=j
- 选择:
- 初态: d p [ 0 ] [ ∗ ] = d p [ ∗ ] [ 0 ] = 0 dp[0][*] = dp[*][0] = 0 dp[0][∗]=dp[∗][0]=0, 但是要考虑第一个字符串开始为 ∗ * ∗号的情况。具体见代码
三、代码
#include
#include
#include
using namespace std;
int dp[24][24];
char s1[24];
char s2[24];
int main()
{
scanf("%s%s", s1, s2);
int l1 = strlen(s1);
int l2 = strlen(s2);
for(int i=0; i<=max(l1, l2); i++)
dp[0][i] = dp[i][0] = 0;
dp[0][0] = 1;
int i=0;
while(s1[i++] == '*' )
dp[i][0] = 1;
for(int i=1; i<=l1; i++)
{
for(int j=1; j<=l2; j++)
{
if(s1[i-1]==s2[j-1] || s1[i-1] == '?')
dp[i][j] = dp[i-1][j-1];
else if(s1[i-1] != s2[j-1] && s1[i-1] == '*')
{
for(int k=0; k<=j; k++)
{
dp[i][j] |= dp[i-1][j-k];
}
}
else
dp[i][j] = 0;
}
}
if(dp[l1][l2])
cout << "matched" << endl;
else
cout << "not matched" << endl;
return 0;
}
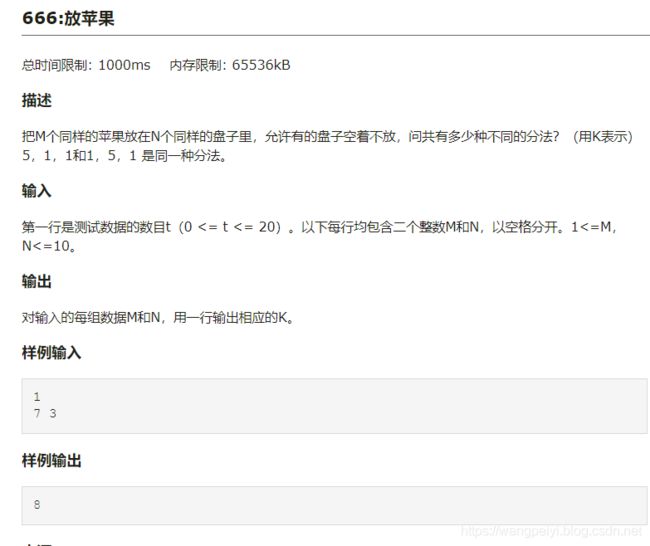
放苹果
三、代码
#include
using namespace std;
const int MAX = 25;
typedef long long ll;
ll dp[MAX][MAX];
int main()
{
int t;
cin >> t;
while(t--)
{
int m, n;
cin >> m >> n;
for(int i=0; i= i)
dp[i][j] = dp[i-1][j] + dp[i][j-i];
else
dp[i][j] = dp[i-1][j];
}
}
cout << dp[n][m] << endl;
}
return 0;
}
最低通行费
三、代码
#include
#include
using namespace std;
const int MAXN = 105;
const int inf = 1 << 30;
int grad[MAXN][MAXN];
int dp[MAXN][MAXN];
int N;
int dfs(int x, int y)
{
if(x > N || y > N)
return inf;
if(dp[x][y] >= 0)
return dp[x][y];
dp[x][y] = grad[x][y]+min(dfs(x+1,y), dfs(x, y+1));
return dp[x][y];
}
int main()
{
cin >> N;
for(int i=1; i<=N; i++)
for(int j=1; j<=N; j++)
cin >> grad[i][j];
memset(dp,-1,sizeof(dp));
dp[N][N] = grad[N][N];
cout << dfs(1, 1) << endl;
}
三角形的最佳路径
#include
using namespace std;
int dp[105][105];
int grad[105][105];
int main()
{
int N;
cin >> N;
for(int i=1; i<=N; i++)
for(int j=1; j<=i; j++)
cin >> grad[i][j];
for(int j=1; j<=N; j++)
dp[N][j] = grad[N][j];
for(int i=N-1; i>=1; i--)
{
for(int j=1; j<=i; j++)
{
dp[i][j] = max(dp[i+1][j], dp[i+1][j+1])+grad[i][j];
}
}
cout << dp[1][1] << endl;
return 0;
}
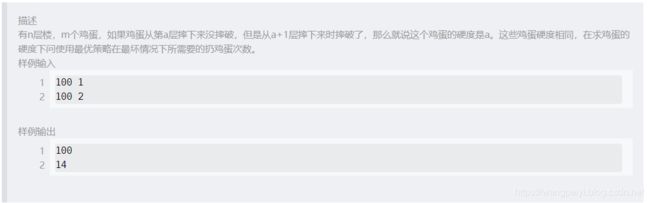
鸡蛋的硬度
- 定义 d p [ i ] [ j ] : dp[i][j]: dp[i][j]:有 i i i层楼 j j j个鸡蛋最坏的次数。
- 目标状态 d p [ n ] [ m ] dp[n][m] dp[n][m]
- 状态转移:
- 选择:
- 前 i i i层可以选择在任意一层扔。
- 在第k层扔可能碎或者没碎。
- 最优策略即选择最优的层 i i i,最坏情况即碎或者没碎中最坏
- 状态转移方程式:
d p [ i ] [ j ] = m i n ( { m a x ( d p [ k − 1 ] [ j − 1 ] , d p [ i − k ] [ j ] ) + 1 ∣ 1 < = k < = i } dp[i][j] = min(\{max(dp[k-1][j-1],dp[i-k][j])+1\quad | \quad 1<=k<=i\} dp[i][j]=min({max(dp[k−1][j−1],dp[i−k][j])+1∣1<=k<=i}
- 选择:
- 初始状态: d p [ i ] [ 1 ] = i , d p [ 0 ] [ j ] = 0 dp[i][1] = i, dp[0][j]=0 dp[i][1]=i,dp[0][j]=0(更新过程不会用到 j = 0 j=0 j=0的状态, 因此不必去定义)
三、代码
#include
#include
using namespace std;
int dp[105][12];
const int inf = 1<<30;
int main()
{
int n, m;
while(cin >> n >> m)
{
for(int i=1; i<=n; i++)
dp[i][1] = i;
for(int j=0; j<=m; j++)
dp[0][j] = 0;
for(int i=1; i<=n; i++)
{
for(int j=2; j<=m; j++)
{
dp[i][j] = inf;
for(int k=1; k<=i; k++)
{
dp[i][j] = min(dp[i][j], max(dp[k-1][j-1],dp[i-k][j])+1);
}
}
}
cout << dp[n][m] << endl;
}
return 0;
}
大盗阿福
- 定义 d p [ i ] dp[i] dp[i]:前 i i i个商店抢劫的最大价值。
- 目标状态 d p [ n ] dp[n] dp[n].
- 状态转移:
- 选择: 抢该商店或者不抢
- 方程式: d p [ i ] = m a x ( d p [ i − 1 ] , d p [ i − 2 ] + a [ i ] ) dp[i] = max(dp[i-1], dp[i-2]+a[i]) dp[i]=max(dp[i−1],dp[i−2]+a[i])
- 初始状态: d p [ 0 ] = 0 , d p [ 1 ] = a [ i ] dp[0] = 0, dp[1] = a[i] dp[0]=0,dp[1]=a[i]
三、代码
#include
#include
using namespace std;
const int MAXM = 100005;
int dp[MAXM], a[MAXM];
int main()
{
int t;
scanf("%d", &t);
while(t--)
{
int n;
scanf("%d", &n);
for(int i=1; i<=n; i++)
scanf("%d", &a[i]);
dp[1] = a[1];
dp[0] = 0;
for(int i=2; i<=n; i++)
dp[i] = max(dp[i-1], dp[i-2]+a[i]);
printf("%d\n", dp[n]);
}
return 0;
}
切割回文
- 定义:
- d p [ i ] : dp[i]: dp[i]: [ 0 , i − 1 ] [0,i-1] [0,i−1]组成的字串需要切成回文需要的最少次数。
- m [ i ] [ j ] : m[i][j]: m[i][j]: [ i , j ] [i,j] [i,j]组成的字串是否是回文。
- 目标状态 d p [ L − 1 ] dp[L-1] dp[L−1].
- 状态转移:
- 选择: 如果 [ 0 , i ] [0,i] [0,i]是回文,则 d p [ i ] = 0 dp[i]=0 dp[i]=0, 如果不是,那么考虑从右到左,第一刀切在哪里.
- 状态转移方程: d p [ i ] = { 0 m [ 0 ] [ i ] = 1 m i n ( { d p [ j ] + 1 ∣ m [ j + 1 ] [ i ] = 1 , 0 < = j < = i − 1 } ) e l s e dp[i] = \begin{cases} 0 & m[0][i]=1 \\ min(\{dp[j]+1\quad | \quad m[j+1][i]=1,0<=j<=i-1\}) & else \end{cases} dp[i]={0min({dp[j]+1∣m[j+1][i]=1,0<=j<=i−1})m[0][i]=1else
- 初态:
- m [ i ] [ i ] = 1 , m [ i ] [ i + 1 ] = ( s [ i ] = = s [ i + 1 ] ) m[i][i]=1, m[i][i+1] = (s[i]==s[i+1]) m[i][i]=1,m[i][i+1]=(s[i]==s[i+1])
- d p [ 0 ] = 0 dp[0]=0 dp[0]=0
三、代码
#include
#include
using namespace std;
const int MAX = 1005;
int is_hui[MAX][MAX];
int dp[MAX];
int main()
{
int T;
cin >> T;
while(T--)
{
string s;
cin >> s;
int L = s.length();
memset(is_hui, 0, sizeof(is_hui));
for(int i=0; i 乘积最大
- 定义 d p [ i ] [ j ] : dp[i][j]: dp[i][j]:前 i i i个数字方 j j j个符号的最大值
- 终态: d p [ n ] [ k ] dp[n][k] dp[n][k]
- 状态转移:
- 选择: 将最后一个符号放在第k个数字之后
- 状态转移方程式: d p [ i ] [ j ] = m a x ( { d p [ k ] [ j − 1 ] ∗ g e t _ n u m ( k + 1 , i ) ∣ j < = k < = i − 1 } ) dp[i][j] = max(\{dp[k][j-1]*get\_num(k+1,i) \quad | \quad j<=k<=i-1\}) dp[i][j]=max({dp[k][j−1]∗get_num(k+1,i)∣j<=k<=i−1})
其中 g e t _ n u m ( i , j ) get\_num(i,j) get_num(i,j)用来求第 i i i位到第 j j j位组成的数字. k > = j k>=j k>=j的原因是需要在前面放 j − 1 j-1 j−1个符号,因此至少需要 j j j个数字。
- 初态: d p [ i ] [ 0 ] = g e t _ n u m ( 1 , i ) dp[i][0]=get\_num(1,i) dp[i][0]=get_num(1,i)
三、代码
#include
#include
using namespace std;
int dp[45][7];
int a[45];
int get_num(int s, int e)
{
int res = 0;
for(int i=s; i<=e; i++)
res = res*10 + a[i];
return res;
}
int main()
{
int n, k;
cin >> n >> k;
for(int i=1; i<=n; i++)
scanf("%1d", &a[i]);
for(int i=1; i<=n; i++)
dp[i][0] = get_num(1,i);
for(int i=2; i<=n; i++)
{
for(int j=1; j 装箱问题
三、代码
#include
#include
using namespace std;
const int MAXV = 20005;
int dp[MAXV];
int a[33];
int main()
{
int V;
cin >> V;
int n;
cin >> n;
for(int i=1; i<=n; i++)
cin >> a[i];
memset(dp, 0, sizeof(dp));
dp[0] = 1;
for(int i=1; i<=n; i++)
for(int j=V; j>=a[i]; j--)
dp[j] = dp[j] | dp[j-a[i]];
int ans = MAXV;
for(int i=V; i>=0; i--)
{
if(dp[i])
ans = min(ans, V-i);
}
cout << ans << endl;
return 0;
}
方格取数
一、题目大意

二、解题思路
(WA):不可以认为先取最大,再去次大。
(AC): 同时模拟两个人行走。
- 定义 d p [ i ] [ j ] [ k ] [ h ] : dp[i][j][k][h]: dp[i][j][k][h]:第一个人走到 ( i , j ) (i,j) (i,j),第二个人走到 ( k , h ) (k,h) (k,h)最优解。
- 目标 d p [ n ] [ n ] [ n ] [ n ] dp[n][n][n][n] dp[n][n][n][n]
- 状态转移:
- 选择: ( i , j , k , h ) (i,j,k,h) (i,j,k,h)可以由 ( i − 1 , j , k − 1 , h ) 、 ( i − 1 , j , k , h − 1 ) , ( i , j − 1 , k − 1 , h ) 、 ( i , j − 1 , k , h − 1 ) (i-1,j,k-1,h)、(i-1,j,k,h-1),(i, j-1,k-1,h)、(i,j-1,k,h-1) (i−1,j,k−1,h)、(i−1,j,k,h−1),(i,j−1,k−1,h)、(i,j−1,k,h−1)转移过来.
- 状态转移方程式 d p [ i ] [ j ] [ k ] [ h ] = { m a x ( 4 个 状 态 的 d p 值 ) + g r a d [ i ] [ j ] + g r a d [ k ] [ h ] ( i , j ) = ( k , h ) m a x ( 4 个 状 态 的 d p 值 ) + g r a d [ i ] [ j ] e l s e dp[i][j][k][h]=\begin{cases} max(4个状态的dp值)+grad[i][j]+grad[k][h] & (i,j)=(k,h) \\ max(4个状态的dp值)+grad[i][j] & else \end{cases} dp[i][j][k][h]={max(4个状态的dp值)+grad[i][j]+grad[k][h]max(4个状态的dp值)+grad[i][j](i,j)=(k,h)else
- 初态:全部置为0即可
三、代码
#include
#include
#include
using namespace std;
int n,i,j,tmp,k,l;
int puz[20][20], dp[20][20][20][20];
int main()
{
scanf("%d",&n);
while(scanf("%d%d%d", &i, &j, &tmp) && i)
puz[i][j] = tmp;
memset(dp, 0, sizeof(dp));
for(int i=1; i<=n; i++)
{
for(int j=1; j<=n; j++)
{
for(int k=1; k<=n; k++)
{
for(int h=1; h<=n; h++)
{
int tmp1 = max(dp[i-1][j][k-1][h], dp[i-1][j][k][h-1]);
int tmp2 = max(dp[i][j-1][k-1][h], dp[i][j-1][k][h-1]);
if(i==k && j == h)
dp[i][j][k][h] = max(tmp1, tmp2) + puz[i][j];
else
dp[i][j][k][h] = max(tmp1, tmp2) + puz[i][j] + puz[k][h];
}
}
}
}
cout << dp[n][n][n][n] << endl;
return 0;
}
滑雪
- 定义 d p [ i ] [ j ] : dp[i][j]: dp[i][j]:为以方格 ( i , j ) (i,j) (i,j)为截止的路线的最长长度。
- 然后脑海中模拟三维立体图像,模拟记忆化搜索过程。
三、代码
#include
#include
using namespace std;
const int MAX = 105;
int dp[MAX][MAX];
int grad[MAX][MAX];
int c, r;
int dir[4][2] = {{1,0},{-1,0},{0,1},{0,-1}};
int dfs(int x, int y)
{
if(dp[x][y] > 0)
return dp[x][y];
dp[x][y] = 1;
for(int i=0; i<4; i++)
{
int nx = x + dir[i][0];
int ny = y + dir[i][1];
if(x < 1 || x > c || y < 1 || y > r)
continue;
if(grad[nx][ny] > grad[x][y])
dp[x][y] = max(dp[x][y], dfs(nx, ny)+1);
}
return dp[x][y];
}
int main()
{
cin >> c >> r;
for(int i=1; i<=c; i++)
for(int j=1; j<=r; j++)
cin >> grad[i][j];
memset(dp, -1, sizeof(dp));
int ans = 0;
for(int i=1; i<=c; i++)
for(int j=1; j<=r; j++)
ans = max(ans, dfs(i,j));
cout << ans << endl;
}
核电站问题
题解
酒鬼
- 定义 d p [ i ] : dp[i]: dp[i]:前 i i i壶酒能喝的最大体积
- 目标状态: d p [ n ] dp[n] dp[n]
- 状态转移:
- 选择: (1)是否喝第 i i i壶酒(2)若喝,是否喝第 i − 1 i-1 i−1壶
- 状态转移方程: d p [ i ] = m a x ( d p [ i − 1 ] , m a x ( d p [ i − 2 ] + a [ i ] , d p [ i − 3 ] + a [ i − 1 ] + a [ i ] ) ) dp[i] = max(dp[i-1], max(dp[i-2]+a[i], dp[i-3]+a[i-1]+a[i])) dp[i]=max(dp[i−1],max(dp[i−2]+a[i],dp[i−3]+a[i−1]+a[i]))
- 初始状态: d p [ 0 ] = 0 , d p [ 1 ] = a [ 1 ] , d p [ 2 ] = a [ 2 ] dp[0]=0, dp[1]=a[1], dp[2]=a[2] dp[0]=0,dp[1]=a[1],dp[2]=a[2]
三、代码
#include
using namespace std;
const int maxn=705;
int dp[maxn];
int a[maxn];
int main()
{
int n;
cin >> n;
for(int i=1; i<=n; i++)
cin >> a[i];
dp[0]=0;
dp[1] = a[1];
dp[2] = a[1] + a[2];
for(int i=3; i<=n; i++)
dp[i] = max(max(dp[i-3]+a[i-1]+a[i],dp[i-2]+a[i]), dp[i-1]);
cout << dp[n] << endl;
return 0;
}
Pku2440 DNA
一、题目大意
长度为 L L L的0-1串,不包含 101 101 101和 111 111 111的子串有多少种
二、解题思路
- 定义: d p [ i ] dp[i] dp[i]:长度为 i i i的串包含合法字串的种数。
- 目标: d p [ n ] dp[n] dp[n]
- 状态转移:
- 选择: (1)第 i i i位是1或0。(2)第 i − 1 i-1 i−1位是1或0
- 状态转移方程: d p [ i ] = d p [ i − 1 ] + d p [ i − 3 ] + d p [ i − 4 ] dp[i] = dp[i-1]+dp[i-3]+dp[i-4] dp[i]=dp[i−1]+dp[i−3]+dp[i−4]
- 初态. d p [ 0 ] = 1 , d p [ 1 ] = 2 , d p [ 2 ] = 4 , d p [ 3 ] = 6 dp[0]=1, dp[1]=2,dp[2]=4, dp[3]=6 dp[0]=1,dp[1]=2,dp[2]=4,dp[3]=6
三、代码
#include
using namespace std;
const int mod = 2005;
int dp[1000000+6];
int main()
{
int n;
cin >> n;
dp[0]=1;
dp[1]=2;
dp[2]=4;
dp[3]=6;
for(int i=4; i<=n; i++)
dp[i] = (dp[i-1]+dp[i-3]+dp[i-4])%mod;
cout << dp[n] << endl;
return 0;
}
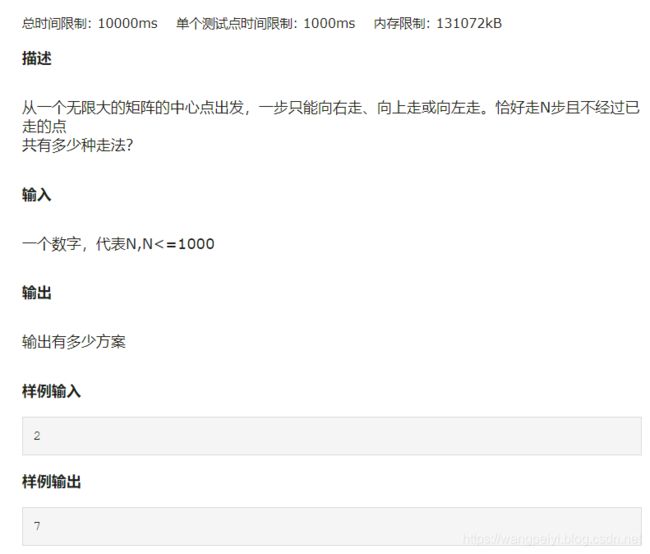
奶牛散步
- 定义 d p [ i ] : dp[i]: dp[i]:走 i i i步的路线数。
- 目标状态 d p [ n ] dp[n] dp[n]
- 状态转移:
- 来源: 走 i i i步来源于走 i − 1 i-1 i−1步后再走一步。这一步可以(1)向上走(2)向左走(3)向右走。
- 若 i − 1 i-1 i−1步的每一个状态都能往三个方向走,则有 d p [ i ] = 3 ∗ d p [ i − 1 ] dp[i]=3*dp[i-1] dp[i]=3∗dp[i−1],但是很明显有一些只能
向上向右或者向上向左走的状态,这样的状态共( d p [ i − 1 ] − d p [ i − 2 ] dp[i-1]-dp[i-2] dp[i−1]−dp[i−2])个其中 d p [ i − 2 ] dp[i-2] dp[i−2]是指 i − 1 i-1 i−1步状态中三个方向都能走的状态(因为它是由 i − 2 i-2 i−2步中左右状态向上走转移过来的)。 - 状态转移方程: d p [ i ] = 2 ∗ d p [ i − 1 ] + d p [ i − 2 ] dp[i]=2*dp[i-1]+dp[i-2] dp[i]=2∗dp[i−1]+dp[i−2]
- 初始状态: d p [ 0 ] = 1 , d p [ 1 ] = 3 dp[0]=1, dp[1]=3 dp[0]=1,dp[1]=3
三、代码
#include
using namespace std;
int main()
{
int dp[1004];
int N;
dp[0]=1;
dp[1]=3;
dp[2]=7;
int n;
cin >> n;
for(int i=3; i<=n; i++)
dp[i] = (2*dp[i-1]+dp[i-2])%12345;
cout << dp[n] << endl;
}
[Usaco2009 Feb]Bullcow
- 定义 d p [ i ] : dp[i]: dp[i]: i i i头牛再条件 k k k的情况下的安排方式。
- 目标状态 d p [ n ] dp[n] dp[n]
- 状态转移:
- 选择: 第 i i i头牛放奶牛还是放公牛。
- 放奶牛: 有 d p [ i − 1 ] dp[i-1] dp[i−1]
- 放公牛: 有 d p [ i − m − 1 ] dp[i-m-1] dp[i−m−1]
- 状态转移方程: d p [ i ] = d p [ i − 1 ] + d p [ i − m − 1 ] dp[i] = dp[i-1]+dp[i-m-1] dp[i]=dp[i−1]+dp[i−m−1]
- 选择: 第 i i i头牛放奶牛还是放公牛。
- 初态: d p [ 0 ] = 1 , d p [ i ] = 1 + i ( i < = m ) dp[0]=1, dp[i]=1+i(i<=m) dp[0]=1,dp[i]=1+i(i<=m)
三、代码
#include
using namespace std;
const int mod = 5000011;
int dp[100000+5];
int n,m;
int main()
{
cin >> n >> m;
dp[0]=1;
for(int i=1; i<=m; i++)
dp[i] = 1 + i;
for(int i=m+1; i<=n; i++)
dp[i] = (dp[i-1]+dp[i-m-1])%mod;
cout << dp[n] << endl;
}
Logs Stacking堆木头
二、解题思路
- 定义状态 d p [ i ] : dp[i]: dp[i]:底层 i i i个木头的堆积方法。
- 目标状态 d p [ n ] dp[n] dp[n]
- 很容易得出递推式: d p [ i ] = d p [ i − 1 ] + 2 ∗ d p [ i − 2 ] + 3 ∗ d p [ i − 3 ] + . . . + ( n − 1 ) ∗ d p [ 1 ] + 1 dp[i] = dp[i-1]+2*dp[i-2]+3*dp[i-3]+...+(n-1)*dp[1]+1 dp[i]=dp[i−1]+2∗dp[i−2]+3∗dp[i−3]+...+(n−1)∗dp[1]+1
- 化简: d p [ i − 1 ] = d p [ i − 2 ] + 2 ∗ d p [ i − 3 ] + . . . + ( n − 2 ) ∗ d p [ 1 ] + 1 dp[i-1]=dp[i-2]+2*dp[i-3]+...+(n-2)*dp[1]+1 dp[i−1]=dp[i−2]+2∗dp[i−3]+...+(n−2)∗dp[1]+1
- 令 s u m [ i ] = d p [ i ] + d p [ i − 1 ] + . . . + d p [ 1 ] sum[i] = dp[i]+dp[i-1]+...+dp[1] sum[i]=dp[i]+dp[i−1]+...+dp[1]
- 则 d p [ i ] = d p [ i − 1 ] + s u m [ i − 1 ] dp[i]=dp[i-1]+sum[i-1] dp[i]=dp[i−1]+sum[i−1]
- 初态: d p [ 0 ] = 1 , s u m [ 0 ] = 0 dp[0]=1, sum[0]=0 dp[0]=1,sum[0]=0