线段树（单点查询+区间求和）无lazy标记

模板题出处
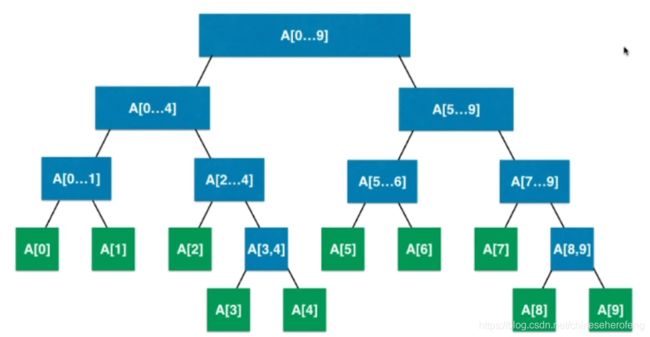
原理就大概如图所示，线段树的每个节点都是原数组的一段区间和，而叶子节点就是原数组对应 的值
建树代码：

void build(int p,int lf,int rt){//建树
    ans[p]=0;
    if(lf==rt) {
        ans[p]=A[lf]; return ;
    }
    int mid=(lf+rt)>>1;
    build(lson);
    build(rson);
    push_up(p);
}

单点修改其实就是一直缩小被修改点所在区间直到区间与修改点重合。
单点修改代码：

void update(int p,int lf,int rt,int pos,int k){//单点修改
    if(lf==rt){
        ans[p]+=k;
        return ;
    }
    int mid=(lf+rt)>>1;
    if(pos<=mid) update(lson,pos,k);
    else update(rson,pos,k);
    push_up(p);//合并更新后节点值
}

欧，对了，上面的push_up操作意思是通过当前区间的左右区间和来计算当前区间的区间和，有点像二叉树后序遍历。
push_up代码：

void push_up(int p){
    ans[p]=ans[p<<1]+ans[p<<1|1];
}

区间求和思想和单点修改思想差不多就是不断逼近目标区间如果当前区间被目标区间完全覆盖则返回线段树当前节点值，（这也是为什么线段是求和比暴力求和香的原因）时间复杂度为（logn）我也不知道怎么算的，orz。。。
区间求和代码：

int sum(int p,int lf,int rt,int l,int r){//区间求和
    if(lf>=l&&rt<=r){//当前查询区间被目标区间完全覆盖
        return ans[p];
    }
    int he=0;
    int mid=(lf+rt)>>1;
    if(l<=mid) he+=sum(lson,l,r);//若当前区间的左区间存在被覆盖的情况则搜左区间
    if(r>mid) he+=sum(rson,l,r);//若当前区间的右区间存在被覆盖的情况则搜右区间
    return he;
}

最后附完整代码：

#include 
using namespace std;
#define int long long
#define lll 500005
#define lson p<<1,lf,mid
#define rson p<<1|1,mid+1,rt
int ans[lll<<1],A[lll]; int n,m;
void push_up(int p){
    ans[p]=ans[p<<1]+ans[p<<1|1];
}
void build(int p,int lf,int rt){//建树
    ans[p]=0;
    if(lf==rt) {
        ans[p]=A[lf]; return ;
    }
    int mid=(lf+rt)>>1;
    build(lson);
    build(rson);
    push_up(p);
}
void update(int p,int lf,int rt,int pos,int k){//单点修改
    if(lf==rt){
        ans[p]+=k;
        return ;
    }
    int mid=(lf+rt)>>1;
    if(pos<=mid) update(lson,pos,k);
    else update(rson,pos,k);
    push_up(p);//合并更新后节点值
}
int sum(int p,int lf,int rt,int l,int r){//区间求和
    if(lf>=l&&rt<=r){//当前查询区间被目标区间完全覆盖
        return ans[p];
    }
    int he=0;
    int mid=(lf+rt)>>1;
    if(l<=mid) he+=sum(lson,l,r);//若当前区间的左区间存在被覆盖的情况则搜左区间
    if(r>mid) he+=sum(rson,l,r);//若当前区间的右区间存在被覆盖的情况则搜右区间
    return he;
}
void chaxun(int a){
    if(a==1){
        int o,p; cin>>o>>p;
        update(1,1,n,o,p);
    }
    if(a==2){
        int x,y; cin>>x>>y;
        int t=sum(1,1,n,x,y);
        cout<<t<<endl;
    }
}
signed main(){
    ios::sync_with_stdio(false);
    cin.tie(0); cout.tie(0);
    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>A[i];
    build(1,1,n);
    for(int i=0;i<m;i++){
        int a; cin>>a;
        chaxun(a);
    }
}