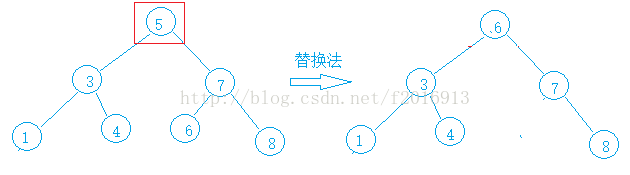
二叉搜索树
一:二叉搜索树的性质:
1:每个节点都有一个作为搜索的关键码(key),所有节点的关键码互不相同;
2:左子树所有节点的关键码(key)都小于右子树的关键码(key)
3 : 左子树所有节点的关键码(key)都小于右子树的关键码(key)
4:左右字子树都是二叉搜索树
二:二叉树的插入:
分三步:
1:空树的情况,直接把节点插入到根节点
2:不为空,比较插入值的关键码与根节点的关键码,确定插入的位置
3:插入后结果任然为一颗二叉搜索树
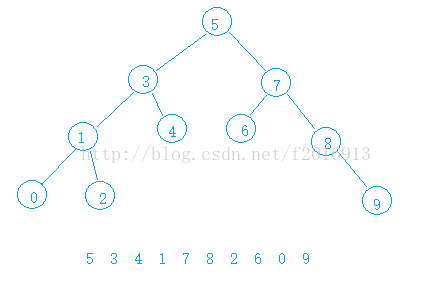
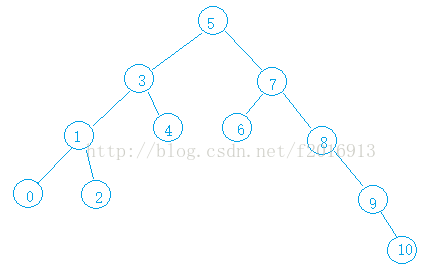
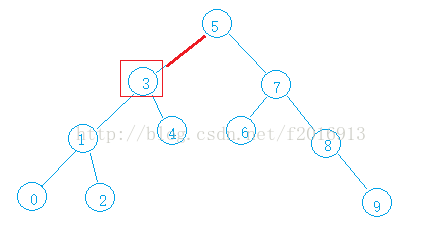
如:我们希望插入10;parent和cur都是从根节点开始,10比5大,走右子树,比7大继续右子树,每次走的一步parent都置为当前值(cur),cur继续向下走,一直到9。最后把值插入到9的后面。
插入后仍然为二叉搜索树
bool Insert(const K&key)
{
//为空
if (_root == NULL)
{
_root = new Node(key);
return true;
}
//不为空
Node*cur = _root;
Node *parent = NULL;
while (cur)
{
if (cur->_key < key)//右边
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key>key)//左边
{
parent = cur;
cur = cur->_left;
}
else
{
return false;//不存在
}
}
//key值存在
Node*tmp = new Node(key);
if (parent->_key < key)//右边
{
parent->_right = tmp;;
}
else //左边
{
parent->_left = tmp;
}
return false;//值相等
}
三:二叉树的查找
1:查找的值与根节点的值比较,从根开始,查找的值比根的值小走左子树,比根的值大走右子树,直到遍历完这个二叉搜索树,结果有两种找到,找不到;
//查找
bool Find(const K&key)
{
Node*cur = _root;
while (cur)
{
if (cur->_key < key)//右边
{
cur = cur->_right;
}
else if (cur->_key >key)//左边
{
cur = cur->_left;
}
else
{
cout << "找到了" <_key<< endl;
return true;
}
}
return false;//没找到
} 
四:二叉树的删除:
删除的算法我们可以分为4种情况:
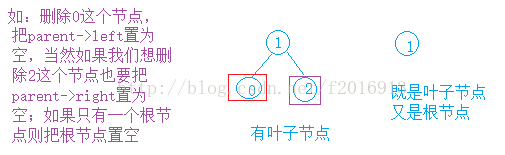
1:删除叶子节点
Node*cur = _root;
Node*parent = NULL;
//叶子节点直接删除
if (cur->_left == NULL)
{
if (parent &&cur == parent->_left)//左为空
{
parent->_left = NULL;
}
else if (parent &&cur == parent->_right)//右为空
{
parent->_right = NULL;
}
else
{
_root = NULL;
}
delete cur;
cur = NULL;
}
2:删除非叶子点
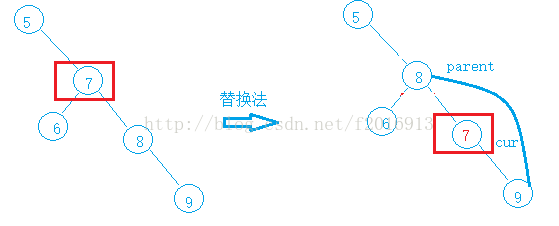
替换法删除找最右孩子的左子树,或者是最左孩子的右子树,,先交换要删除的节点与其右孩子交换,然后把要删除的节点右孩子赋给父亲的右孩子。最后删除当前结点。
3: 删除根节点;
4:删除所有节点;
删除算法:
bool Remove(const K&key)
{
//为空
if (_root == NULL)
{
return false;
}
//不为空
Node*cur = _root;
Node*parent = NULL;
while (cur)
{
if (cur->_key < key)//右边
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key>key)//左边
{
parent = cur;
cur = cur->_left;
}
//要删除的节点就是当前节点
else
{
//叶子节点直接删除
if (cur->_left == NULL)
{
if (parent &&cur == parent->_left)//左为空
{
parent->_left = NULL;
}
else if (parent &&cur == parent->_right)//右为空
{
parent->_right = NULL;
}
else
{
_root = NULL;
}
delete cur;
cur = NULL;
}
//只有一个孩子节点
else if (cur->_left == NULL || cur->_right == NULL)
{
if (cur->_left != NULL)//只有左孩子
{
if (parent == NULL)
{
_root = cur->_left;
}
else if (parent->_left = cur)//左子树
{
parent->_left = cur->_left;
}
else
{
parent->_right = cur->_left;
}
delete cur;
}
else if (cur->_right != NULL)//只有右孩子
{
if (parent == NULL)
{
_root = cur->_right;
}
else if (parent->_right == cur)
{
parent->_left = cur->_right;
}
else
{
parent->_right = cur->_right;
}
delete cur;
}
}
//有两个孩子(替换法删除)找最右孩子的左子树
else
{
Node* subRight = cur->_right;
Node* subParent = cur;
Node*del = NULL;
while (subRight->_left)
{
subParent = subRight;
subRight = subRight->_left;
}
cur->_key = subRight->_key;
if (subParent->_right == subRight)
subParent->_right = subRight->_right;
else
subParent->_left = subRight->_left;
delete subRight;
}
return true;
}
}
return false;
}//没有找到删除值完整代码:
.h文件
#pragma once
#include
using namespace std;
template
struct BinarySerachTreeNode
{
K _key;
BinarySerachTreeNode *_left;
BinarySerachTreeNode *_right;
BinarySerachTreeNode(const K&key)
:_key(key)
, _left(NULL)
, _right(NULL)
{}
};
template < class K>
class BinarySerachTree
{
typedef BinarySerachTreeNode Node;
public:
BinarySerachTree()
:_root(NULL)
{}
//插入
bool Insert(const K&key)
{
//为空
if (_root == NULL)
{
_root = new Node(key);
return true;
}
//不为空
Node*cur = _root;
Node *parent = NULL;
while (cur)
{
if (cur->_key < key)//右边
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key>key)//左边
{
parent = cur;
cur = cur->_left;
}
else
{
return false;//不存在
}
}
//key值存在
Node*tmp = new Node(key);
if (parent->_key < key)//右边
{
parent->_right = tmp;;
}
else //左边
{
parent->_left = tmp;
}
return true;
}
//查找
bool Find(const K&key)
{
Node*cur = _root;
while (cur)
{
if (cur->_key < key)//右边
{
cur = cur->_right;
}
else if (cur->_key >key)//左边
{
cur = cur->_left;
}
else
{
cout << "找到了" <_key<< endl;
return true;
}
}
return false;//没找到
}
//删除
bool Remove(const K&key)
{
//为空
if (_root == NULL)
{
return false;
}
//不为空
Node*cur = _root;
Node*parent = NULL;
while (cur)
{
if (cur->_key < key)//右边
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key>key)//左边
{
parent = cur;
cur = cur->_left;
}
//要删除的节点就是当前节点
else
{
//叶子节点直接删除
if (cur->_left == NULL)
{
if (parent &&cur == parent->_left)//左为空
{
parent->_left = NULL;
}
else if (parent &&cur == parent->_right)//右为空
{
parent->_right = NULL;
}
else
{
_root = NULL;
}
delete cur;
cur = NULL;
}
//只有一个孩子节点
else if (cur->_left == NULL || cur->_right == NULL)
{
if (cur->_left != NULL)//只有左孩子
{
if (parent == NULL)
{
_root = cur->_left;
}
else if (parent->_left = cur)//左子树
{
parent->_left = cur->_left;
}
else
{
parent->_right = cur->_left;
}
delete cur;
}
else if (cur->_right != NULL)//只有右孩子
{
if (parent == NULL)
{
_root = cur->_right;
}
else if (parent->_right == cur)
{
parent->_left = cur->_right;
}
else
{
parent->_right = cur->_right;
}
delete cur;
}
}
//有两个孩子(替换法删除)找最右孩子的左子树
else
{
Node* subRight = cur->_right;
Node* subParent = cur;
Node*del = NULL;
while (subRight->_left)
{
subParent = subRight;
subRight = subRight->_left;
}
cur->_key = subRight->_key;
if (subParent->_right == subRight)
subParent->_right = subRight->_right;
else
subParent->_left = subRight->_left;
delete subRight;
}
return true;
}
}
return false;
}//没有找到删除值
//中序
void InOrder()
{
_InOrder(_root);
cout << endl;
}
protected:
void _InOrder(Node*root)
{
Node*cur = root;
if (cur == NULL)
{
return ;
}
_InOrder(cur->_left);
cout << cur->_key << " ";
_InOrder(cur->_right);
}
protected:
Node* _root;
};
void TestBinarySearchTree()
{
BinarySerachTree b;
int a[] = { 5, 3, 4, 1, 7, 8, 2, 6, 0, 9 };
for (int i = 0; i