第七届蓝桥杯省赛--方格填数--DFS或全排列

 

第七届其他题目解析链接

 

答案是 1580

 

思路

两个做法  DFS或者全排列  （全排列要好写些）

 

DFS

一共10个位置  10个数

第一个位置 可以放0-9   接下来的位置要满足相邻位置不连续   所以我们dfs搜索所有可能的方案并计数

 

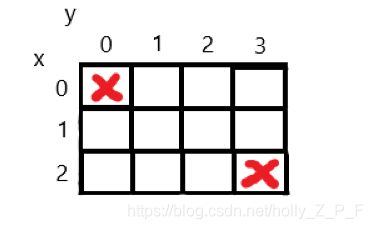
我们先建立坐标  如图所示

然后 我们DFS的方向需要注意一下  

这个题的解法巧妙就在于我们 DFS的顺序

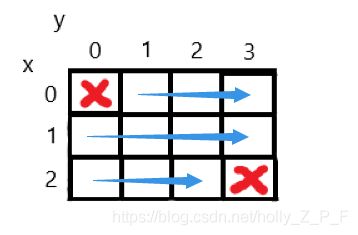
我们按照从左到右的方向去DFS

走到最右边的时候  我们不往下走   而是另起一行 继续从左往右   如图

为什么这么做呢 ？

这样做可以大大降低DFS的复杂度   好处如下（可以结合代码去看比较好理解）

1、我们DFS的时候 可以有四个探测方向  但是按照这样做就只有向右探测一个方向了  到头了就另起一行

 

2、依据题意  我们在给一个位置放数字的时候 需要判断他的八个方向  看看相邻数字是否连续  但是我们用这种顺序去DFS就只用判断四个方向  左  左上  上  右上  因为按照这个顺序去填数  所填位置的下边和右边还没到呢  所以不用考虑下（左下  右下  正下）和右 

 

3、注意开头和结尾  （0，0）和（2，3）这两个位置是不能填数的   那么你判断边界的时候怎么判断呢  如果你以0<=x<=2 和0<=y<=3来判断呢是无法判断到（0，0）和（2，3）的  需要特判 ，而我们用这种dfs顺序呢，我们不需要特判。开头我们直接从（0，1）开始，避过了（0，0）。而结尾（2，3）刚好说明我们填数结束了，此时计数顺便结束递归就好了

ps：两个小细节

1、往左走是 (x,y-1)  左上走是(x-1,y-1)  正上是(x-1,y)  所以我们用一个转向数组，

int dir[4][2]={{0,-1},{-1,-1},{-1,0},{-1,1}};//x y分别加上  就代表左 左上  上 右上

2、要求数字不连续  我们直接判断差的绝对值大于一就好了

代码 及注释

#include
#include
#include
#include
#include
using namespace std;
int a[4][4];
int vis[11];
int cnt=0;
bool check(int x,int y,int v){
    //转向
    int dir[4][2]={{0,-1},{-1,-1},{-1,0},{-1,1}};//左 左上  上 右上
    for(int i=0;i<4;i++){
        int xx=x+dir[i][0];
        int yy=y+dir[i][1];
        if(xx<3 && xx>=0 && yy<4 && yy>=0){
            if(abs(a[xx][yy]-v)==1)return false;
        }
    }
    return true;
}
void DFS(int x,int y){
    if(x==2&&y==3){cnt++;return;}//遇到（2，3）说明结束
    
    for(int i=0;i<=9;i++){
        //要确保这个数没被选过并且放在这里符合题意
        if(vis[i]==0&&check(x,y,i)){
        
            vis[i]=1;a[x][y]=i;
    
            if(y+1<4) DFS(x,y+1);//向右搜索
            else DFS(x+1,0);//另起一行
            
            vis[i]=0;
        }
    }
    return ;
}
int main(){
    for(int i=0;i<4;i++)//初始化一个较小的数
        for(int j=0;j<4;j++)
            a[i][j]=-20;
            
    DFS(0,1);//从（0，1）开始
    printf("%d\n",cnt);
    return 0;
}

 

全排列做法

这个做法比DFS要好写些

一共只有10个空位  位置是固定的  数字呢就是0-9   我们把0-9做个全排列  那么所有的填数方案就出来了

筛选出符合要求的  记下来就好了

#include
#include
#include
#include
#include
using namespace std;
int a[11]={0,1,2,3,4,5,6,7,8,9};
bool c(int x,int y){
    if(abs(x-y)==1)return false;
    else return true;
}
int main(){
    int cnt=0;
    do{
        if(c(a[1],a[0]))
        if(c(a[2],a[1]))
        if(c(a[3],a[0]))
        if(c(a[4],a[3])&&c(a[4],a[0])&&c(a[4],a[1]))
        if(c(a[5],a[4])&&c(a[5],a[0])&&c(a[5],a[1])&&c(a[5],a[2]))
        if(c(a[6],a[5])&&c(a[6],a[1])&&c(a[6],a[2]))
        if(c(a[7],a[3])&&c(a[7],a[4]))
        if(c(a[8],a[7])&&c(a[8],a[3])&&c(a[8],a[4])&&c(a[8],a[5]))
        if(c(a[9],a[8])&&c(a[9],a[4])&&c(a[9],a[5])&&c(a[9],a[6]))
        cnt++;
    }while(next_permutation(a,a+10));
    printf("%d\n",cnt);
    return 0;
}