CodeForces Round#628 赛后题解

Codeforces round 628赛后解题报告

A. EhAb AnD gCd

首先，我们要来了解一些性质，以及 LCM 和 GCD 的一些特殊关联，我们从他们的定义入手：
首先，我们设：
$$a={\Pi }_{i=1}{p}_i^{c_i},b={\Pi }_{i=1}{p}_i^{d_i}$$
其中，$p_i$ 代表质数。这样，我们就有：
$$gcd(a,b)={\Pi }_{i=1}{p}_i^{\min (c_i,d_i)}$$
$$lcm(a,b)={\Pi }_{i=1}{p}_i^{\max (c_i,d_i)}$$
由于我们知道：对于任意两个数 $x,y$，都有 $x+y=\min (x,y)+\max (x,y)$，因此：
$$a\cdot b=gcd(a,b)\cdot lcm(a,b)$$

所以对于这道题，我们知道了 $gcd(a,b)+lcm(a,b)=x$，而且 $a\cdot b=gcd(a,b)\cdot lcm(a,b)$，所以当 $a=1,b=x-1$ 时，这两个条件同时满足，所以只要输出 $1,x-1$ 即可。

//#pragma GCC optimize("Ofast","-funroll-loops","-fdelete-null-pointer-checks")
//#pragma GCC target("ssse3","sse3","sse2","sse","avx2","avx")
#include
using namespace std;

int read() {
	char ch=getchar();
	int f=1,x=0;
	while(ch<'0'||ch>'9') {
		f=-1;
		ch=getchar();
	}
	while(ch>='0'&&ch<='9') {
		x=x*10+ch-'0';
		ch=getchar();
	}
	return f*x;
}

int n;

signed main() {
	
	int t;
	t=read();
	while(t--) {
		n=read();
		cout<<1<<" "<<n-1<<endl;
	} 
	return 0;
}

B. CopyCopyCopyCopyCopy

对于这样一道题来说，因为是在复制了 $n$ 次的数列里取数，所以真正把数列列出来，然后 DP 地算法，时间复杂度超太多，不现实，所以我们考虑贪心。

因为是复制了 $n$ 次的数列，所以我们甚至可以在每一个数列里取一个数，最后凑成原数列，所以这告诉我们，原数列的任意全排列皆可以取到，所以只要对于原数列去重后，把元素个数输出即可。

//#pragma GCC optimize("Ofast","-funroll-loops","-fdelete-null-pointer-checks")
//#pragma GCC target("ssse3","sse3","sse2","sse","avx2","avx")
#include
#define int long long
using namespace std;

int read() {
	char ch=getchar();
	int f=1,x=0;
	while(ch<'0'||ch>'9') {
		f=-1;
		ch=getchar();
	}
	while(ch>='0'&&ch<='9') {
		x=x*10+ch-'0';
		ch=getchar();
	}
	return f*x;
}

const int maxn=1e5+10; 

int n,a[maxn];

signed main() {
	
	int t;
	t=read();
	while(t--) {
		n=read();
		map<int,bool> m;
		int ans=0;
		for(int i=1;i<=n;i++) {
			a[i]=read();
			if(!m[a[i]]) ans++;
			m[a[i]]=1;
		}
		cout<<ans<<endl;
	}
	return 0;
}

C. Ehab and Path-etic MEXs

首先这道题我读了20min才读懂

闲话不多说，我们先来看题。通过思考，我们发现，其实我们只需要考虑边权为 $0,1,2$ 的边。为什么呢？首先，我们来讲一个废话真命题：对于任意两条边，他们肯定同时出现在一条也是唯一一条链上。

因此我们发现，题目中所提到的 ${\max }_{(u,v)\in E}MEX(u,v)$，无论如何，最小值至少为2，因为 $0,1$ 肯定出现在一条链上。而对于答案是否大于 $2$，我们就要分析边权为 $2$ 的这条边了。所以，为了使 $0,1,2$，不再一条链上，我们需要找到如下图的“T型” ，如果能找到，那么答案就为2，找到一个“T型”，然后把 $0,1,2$ 分别放上去即可。

但如果找不到呢？是不是要考虑 $3$？

其实不用，如果找不到“T型”，那么，这棵树就退化成了一条链，那么所有边在一条链上（也只有一条链），所以边权随意乱放，答案也都一样。这道题就分析完了。

//#pragma GCC optimize("Ofast","-funroll-loops","-fdelete-null-pointer-checks")
//#pragma GCC target("ssse3","sse3","sse2","sse","avx2","avx")
#include
#define int long long
using namespace std;

int read() {
	char ch=getchar();
	int f=1,x=0;
	while(ch<'0'||ch>'9') {
		f=-1;
		ch=getchar();
	}
	while(ch>='0'&&ch<='9') {
		x=x*10+ch-'0';
		ch=getchar();
	}
	return f*x;
}

const int maxn=1e5+10;

int n,ans[maxn];
vector<int> bi[maxn];


signed main() {
	
	n=read();
	fill(ans,ans+n+1,-1);
	for(int i=1;i<n;i++) {
		int a=read(),b=read();
		bi[a].push_back(i);
		bi[b].push_back(i);
	}
	int now=0;
	for(int i=1;i<=n;i++) {
		if(bi[i].size()>=3) {
			for(int j=0;j<3;j++) {
				ans[bi[i][j]]=j;
			}
			now=3;
			break;
		}
	}
	for(int i=1;i<n;i++) {
		if(ans[i]==-1) {
			ans[i]=now++;
		}
	}
	for(int i=1;i<n;i++) {
		cout<<ans[i]<<endl;
	}
	return 0;
}

D. Ehab the Xorcist

这道题是一个纯数学的题，首先我们来看:如果 $u>v$ 输出 $-1$，因为 $xor$ 操作只会然数变小，不会变大，所以得证。然后我们会发现，答案数组的元素数不会超过 $3$，因为对于一个三元组：$(u,\frac{(v-u)}{2},\frac{(v-u)}{2})$,永远满足题目要求（因为 $axora=0$）所以我们需要考虑的就是什么情况下答案为 $0,1,2$。我们一次来分析。

对于 $0$，当 $u=v=0$ 时，答案是 $0$，样例已给出。
对于 $1$，很好说，就是当 $u=v\ne 0$ 时，答案数组为 $u$，元素个数为 $1$。
对于 $2$ 来说，就是一个数对 $(a,b)$ 满足：$a+b=v,axorb=u$，由于我们知道：$a+b=axorb+2\cdot (a\&b)$，所以 $a\&b=\frac{(v-u)}{2}$。这是一个惊人的发现。我们再来对这些数以二进制的形式一点一点分析，我们设：$x=\frac{v-u}{2}$。如果对于 $x$ 来说，在第 $i$ 位上是 $1$，那么 $a,b$ 这一位上都是 $1$，然后我们就可以发现，$u$ 的第 $i$ 位上就是 $0$。然而只有当 $a,b$ 某一位上都是 $0$，$u,x$ 在这一位上的数值也都是 $0$。这也是他们在某一位上唯一可能相等的情况。所以，如果 $x\&u\ne 0$，那么答案就为 $3$，否则答案可以为 $2$。我们继续分析，由于之前说过：$a+b=axorb+2\cdot (a\&b)$，然而现在 $x\&u=0$，所以 $x+u=xxoru$，因此 $(u+x,x)$ 是一组可行的二元组。

//#pragma GCC optimize("Ofast","-funroll-loops","-fdelete-null-pointer-checks")
//#pragma GCC target("ssse3","sse3","sse2","sse","avx2","avx")
#include
#define int long long
using namespace std;

int read() {
	char ch=getchar();
	int f=1,x=0;
	while(ch<'0'||ch>'9') {
		f=-1;
		ch=getchar();
	}
	while(ch>='0'&&ch<='9') {
		x=x*10+ch-'0';
		ch=getchar();
	}
	return f*x;
}

int n;

signed main() {
	
	n=1;
	for(int i=1;i<=n;i++) {
		int u=read();
		int v=read();
		
		if(v<u){
			cout<<-1<<endl;
		}
		else if(u==0&&v==0) {
			cout<<0<<endl;
		}
		else if(u==v) {
			cout<<1<<endl;
			cout<<u<<endl;
		}
		else if(u%2==v%2) {
			int p=(v-u)/2,q=(u+v)/2;
			if((p^q)==u) {
				cout<<2<<endl;cout<<((v-u)/2)<<" "<<(u+v)/p,2<<endl;
			}
			else {
				cout<<3<<endl;cout<<u<<" "<<(v-u)/2<<" "<<(v-u)/2<<endl;
			}
		}
		else {
			cout<<-1<<endl;
		}
	}
	return 0;
}

E. Ehab’s REAL Number Theory Problem

这，也是一道纯数论题，首先题目里有一句很重要的话：“every element in this array has at most 7 divisors”，然而我们知道，如果 $p$ 表示质数，则：
$$a={\Pi }_{i=1}{p}_i^{c_i}$$

所以 $a$ 共有：
$${\Pi }_{i=1}{c}_i+1$$
个约数，然而这道题里的数，至多有 $7$ 个约数，这代表，这道题里给出的数一定能用（$p,q$ 为质数）：
$$a=p^x\cdot q^y$$
每个数最多只有两个不同质因子，这样这个就简单很多了。

我们不难想到，可以对 $p,q$ 建边，若果 $x,y$ 中有一个为0，那么就把另一个对应的底数与 $1$ 相连。所以，对于样例3来说，就是这样的图：

发现了什么？这是一个环！！！所以在这样的图里，任意一个环，都代表着一个完全平方数的诞生，所以我们只需要找到最小环即可。

但为什么呢？我们发现，我们可以把每一条边想象成一个数，每次走过这条边，就相当于我们用了这个数。所以通过这条边，也相当于在最后我们所需要的形成的那个完全平方数上把其两个节点的编号乘上去。所以只要形成了环，那么每个节点被乘上去的次数就为 $2$，这样我们最后得到一个完全平方数。由于我们要找的数，越少越好，所以求得就算是最小环。

但是还有一个问题：最小环算法是 $O(n^2)$ 的，会超时。其实我们只需要从编号 $\le \sqrt{\max a_i}$ 即可，这个可以给读者思考为什么。算法的时间复杂度就降到了 $O(p(n)\cdot p(\max a_i))$，$p(x)$ 指小于等于 $x$ 的质数的个数。

//#pragma GCC optimize("Ofast","-funroll-loops","-fdelete-null-pointer-checks")
//#pragma GCC target("ssse3","sse3","sse2","sse","avx2","avx")
#include
#define int long long
using namespace std;

int read() {
	char ch=getchar();
	int f=1,x=0;
	while(ch<'0'||ch>'9') {
		f=-1;
		ch=getchar();
	}
	while(ch>='0'&&ch<='9') {
		x=x*10+ch-'0';
		ch=getchar();
	}
	return f*x;
}

const int maxn=1e5+10; 

struct edge {
	int v,next;
}e[maxn<<3];

int n,h[maxn*10],cnt,a[maxn],prime[maxn],p_cnt,dis[maxn*10];
vector<int> p[maxn*10];
bool isp[maxn*10],calc[maxn*10];

void addedge(int u,int v) {
	e[cnt].v=v;
	e[cnt].next=h[u];
	h[u]=cnt++;
}

void init(int x)  {
	int xx=sqrt(x),rec=x;
	for(int i=2;i<=xx;i++) {
		if(x%i==0) {
			int num=0;
			while(x%i==0) {
				x/=i;
				num++;
			}
			if(num&1) {
				p[rec].push_back(i);
			}
		}
	}
	if(isp[x]) {
		p[rec].push_back(x);
	}
}
void find_prime(int x) {
	fill(isp+1,isp+x+1,1);
	isp[1]=isp[0]=0;
	for(int i=2;i<=x;i++) {
		if(isp[i]) {
			prime[p_cnt+1]=i;
			p_cnt++;
		}
		for(int j=1;j<=p_cnt;j++){
			if(i*prime[j]>x) break;
			isp[i*prime[j]]=0;
			if(prime[j]%i==0) {
				break;
			}
		}
	}
}

signed main() {
	
	n=read();
	int maxx=-1;
	for(int i=1;i<=n;i++) {
		a[i]=read();
		maxx=max(maxx,a[i]);
	}
	find_prime(maxx);
	fill(h+1,h+1+maxx,-1);
	for(int i=1;i<=n;i++) {
		if(!calc[a[i]])
			init(a[i]);
		calc[a[i]]=1;
	} 
	
	for(int i=1;i<=n;i++) {
		if(p[a[i]].empty()) {
			cout<<1<<endl;
			return 0;
		}
		if(p[a[i]].size()==1) {
			p[a[i]].push_back(1);
		}
		addedge(p[a[i]][1],p[a[i]][0]);
		addedge(p[a[i]][0],p[a[i]][1]);
	}
	
	int ans=2e9;
	prime[0]=1;
	for(int i=0;i<=p_cnt;i++) {
		if(prime[i]*prime[i]>maxx) {
			break;
		}
		queue<pair<int,int> > q;
		fill(dis+1,dis+maxx+1,1e9);
		q.push(make_pair(prime[i],-1));
		dis[prime[i]]=0;
		
		while(!q.empty()) {
			pair<int,int> p=q.front();
			q.pop();
			int u=p.first,fa=p.second;
			
			for(int j=h[u];~j;j=e[j].next) {
				int v=e[j].v;
				if(j!=fa&&j!=(fa^1)) {
					if(dis[v]==1e9&&v!=prime[i]) {
						q.push(make_pair(v,j));
						dis[v]=dis[u]+1;
					}
					else {
						ans=min(ans,dis[u]+dis[v]+1);
					}
				}
			}
		}
	}
	
	printf("%lld",ans==2e9? -1:ans);
	return 0;
}

F. Ehab’s Last Theorem

最后一道题，很有质量，是一道好的图论题。

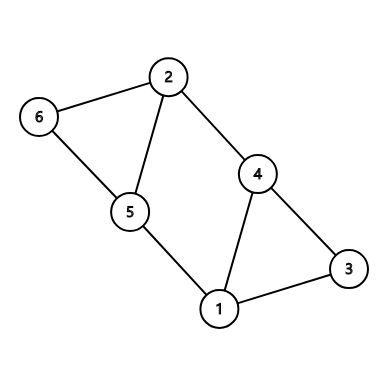
我们定义 $sq=\lceil \sqrt{n}\rceil$。我们把原题中样例2的图搬过来作为举例：

首先，我们随便以一个点作为起点进行 DFS。我们以1位起点。那么，我把DFS中经过过的边（也就是DFS树），边权为 $1$，其他为 $0$。那么原图就变成了这个样子：

)

我们发现，由 $1$ 边构成的图是一棵树，虽然这个性质对我们的解题毫无用处，但这个DFS树真的是没什么用，了解就好，他对我们的思路启发是有一点作用的。我们继续讲题，现在，如果在DFS时，我们从 $u$ 出发，找到了一个点 $v$，如果之前 $v$ 已经被搜到过了，而且 $u,v$ 的在DFS树上深度差大于等于 $sq-1$，就可以找到一个长度至少为 $sq$ 的环，就可以回答第二个问题了。如果没有这样的边，那么我们一定可以回答的一个问题，具体证明很简单，这里不再赘述，应该是一个小学奥数的证明吧。

所以我们就可以快乐地写代码啦！

//#pragma GCC optimize("Ofast","-funroll-loops","-fdelete-null-pointer-checks")
//#pragma GCC target("ssse3","sse3","sse2","sse","avx2","avx")
#include
#define int long long
using namespace std;

int read() {
	char ch=getchar();
	int f=1,x=0;
	while(ch<'0'||ch>'9') {
		f=-1;
		ch=getchar();
	}
	while(ch>='0'&&ch<='9') {
		x=x*10+ch-'0';
		ch=getchar();
	}
	return f*x;
}

const int maxn=1e5+10;

int n,cnt,h[maxn],d[maxn],sq,m;
set<pair<int,int> > s;
vector<int> ans;
bool vis[maxn];

struct edge {
	int v,next;
}e[maxn<<2];

void addedge(int u,int v) {
	e[++cnt].next=h[u];
	e[cnt].v=v;
	h[u]=cnt;
} 

void dfs(int u,int father) {
	d[u]=d[father]+1;
	ans.push_back(u);
	for(int i=h[u];i;i=e[i].next) {
		int v=e[i].v;
		if(!d[v]) {
			dfs(v,u);
		}
		if(d[u]-d[v]+1>=sq) {
			printf("2\n%lld\n",d[u]-d[v]+1);
			for(int i=d[v]-1;i<d[u];i++) {
				cout<<ans[i]<<" ";
			}
			exit(0);
		}
	}
	if(!vis[u]) {
		for(int i=h[u];i;i=e[i].next) {
			vis[e[i].v]=1;
		}
	}
	ans.pop_back();
} 

signed main() {
	
	n=read(),m=read();
	sq=ceil(sqrt(n));
	for(int i=1;i<=m;i++) {
		int a=read(),b=read();
		addedge(a,b);
		addedge(b,a);
	}
	dfs(1,0);
	cout<<1<<endl;
	int tot=1;
	for(int i=1;tot<=sq;++i)  {
		if(!vis[i]) {
			printf("%d ", i);
			tot++;
		}
	}
	return 0;
}