第0周周赛——极限手速赛(题解)之上篇
A题:
A题题目链接
题目描述:
这道题是一血
什么?这道题竟然没有题目描述?
输入只有一行,包含一个整数n (2 ≤ n ≤ 2·1018)
输出5n的后两位.
2
25
这道题属于签到题系列的,注意一下n的范围就好。
完整代码实现:
#include
#include
typedef long long ll;
int main()
{
ll n;
while(scanf("%I64d",&n)==1&&n)
{
printf("25\n");
}
return 0;
}
B题题目链接
题目描述:
我的小金库
这道题总算有题目描述了
你有n块钱,每秒后你的钱会是上一秒的1.000000011倍(这真是太爽了),问t秒之后,你的钱变多少了?(到时候拿利息去买个妹子)
输入只有一行包含整数n (1000 ≤ n ≤ 10 000)和整数t (0 ≤ t ≤ 2 000 000 000)
输出一个数,表示t秒后你将拥有的钱的总数,输出与标准答案的相对误差不超过10 - 6视为正确答案.
相对误差:假如你的答案是a,而标准答案是b,如果视为正确
1000 1000000
1011.060722383550382782399454922040
这道题出的不太好,直接用pow函数计算即可得出答案,题目原意应该不是这样,我自己的做法是先用log函数降阶,求出指数,然后再调用pow函数即可。
完整代码实现:
#include
#include
#include
int main()
{
double n,t;
while(scanf("%lf%lf",&n,&t)==2)
{
double exp = log10(n) + t * log10(1.000000011);
printf("%.20f\n",pow(10,exp));
}
return 0;
} C题:
C题题目链接
题目描述:
幸运树
what?你说什么?幸运树?
是幸运数吧。。没文化,真可怕
幸运树(不...是幸运数)是一个只包含数字7和数字8的数。
输入只有一行,包含一个整数 n (1 ≤ n ≤ 55) — 表示数的最大位数(位数:例如1是一位数,23是两位数)
输出一个整数,表示在n位之内(包括n)的幸运数的个数
2
6
幸运数是只含7和8的数字,那么当只有一位的时候,有7和8,两位的时候有77,78,87,88,三位的时候有777,778,787,788,877,878,887,888
枚举到这里我们发现,其实这是一个排列的问题,比如说该数有三位
那么第一位的选择有2种,第二位也是,第三位同样如此,所以根据乘法原理计算得总的选择有2*2*2 = 8种
而题设中问的是n位之内幸运数的个数,那么for循环遍历一遍再叠加即可
完整代码实现:
#include
#include
#include
typedef unsigned long long ull;
int main()
{
int n;
while(scanf("%d",&n)==1&&n)
{
ull ans = 0;
for(int i = 1;i <= n;i++)
ans += (ull)pow(2,i);
printf("%I64u\n",ans);
}
return 0;
}
D题题目链接
题目描述:
这道题简直让翻译的工作人员罢工
输入只有一行,包含一个整数n (0 ≤ n ≤ 109).
输出只有一行,包含一个整数,表示编号在n之内(包括n)的小六边形的个数
2
19
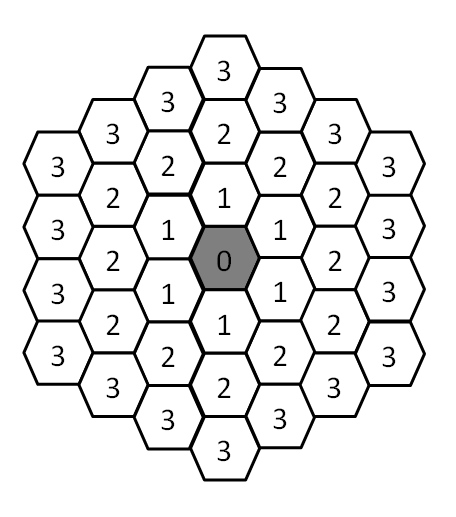
很明显,这是一道找规律的题目,我们可以看图找规律。
图中正中间小六边形的序号为0
然后外围第一层是6个序号为1的小六边形,外围第二层通过计算得有12个序号为2的小六边形,外围第三层有18个序号为3的小六边形,那么这时我们就找到规律了
序号在n之内的小六边形的总个数为:1+6*1+6*2+....+6*n
于是我们很容易想到用for循环累加即可,但是这道题需要注意的一个地方是:n的数据范围到达了10^9次方,所以这样做的话必然超时。
而这个表达式的后缀是一个等差数列,所以我们不必要用for循环累加,只需要直接计算出结果即可,将时间复杂度降至O(1)。
完整代码实现:
#include
#include
typedef unsigned long long ull;
int main()
{
ull n;
while(scanf("%I64u",&n)==1)
{
ull ans = 3*n*(n+1) + 1;
printf("%I64u\n",ans);
}
return 0;
}
E题题目链接
题目描述:
Developing tools for creation of locations maps for turn-based fights in a new game, Petya faced the following problem.
A field map consists of hexagonal cells. Since locations sizes are going to be big, a game designer wants to have a tool for quick filling of a field part with identical enemy units. This action will look like following: a game designer will select a rectangular area on the map, and each cell whose center belongs to the selected rectangle will be filled with the enemy unit.
More formally, if a game designer selected cells having coordinates (x1, y1) and (x2, y2), where x1 ≤ x2 and y1 ≤ y2, then all cells having center coordinates (x, y) such that x1 ≤ x ≤ x2 and y1 ≤ y ≤ y2 will be filled. Orthogonal coordinates system is set up so that one of cell sides is parallel to OX axis, all hexagon centers have integer coordinates and for each integer x there are cells having center with such x coordinate and for each integer y there are cells having center with such y coordinate. It is guaranteed that difference x2 - x1 is divisible by 2.
Working on the problem Petya decided that before painting selected units he wants to output number of units that will be painted on the map.
Help him implement counting of these units before painting.
输入只有一行,包含四个整数x1, y1, x2, y2 ( - 109 ≤ x1 ≤ x2 ≤ 109, - 109 ≤ y1 ≤ y2 ≤ 109) — 表示两个正六边形的中心坐标
输出只有一行,包含一个整数——表示有多少个正六边形将会被涂上颜色。
1 1 5 5
13
在图中选定两个正六边形中心的坐标(x1, y1)和(x2, y2),(x1 ≤ x2并且y1 ≤ y2),所有的含有中心坐标(x, y) 并且x1 ≤ x ≤ x2 和 y1 ≤ y ≤ y2(两个条件均要满足)的正六边形就会被涂上颜色。图中建立了正交坐标系,所以所有正六边形的一侧将会平行于Ox轴,每个整数x和每个整数y均是某个正六边形的中心坐标,保证(x2 - x1)能够整除2,保证每个正六边形的中心坐标均为整数。
解析:
这道题其实不难,但是由于是英文题,而且题目冗长,所以可能会给人带来阅读的困难,但是我们只需要看图找规律即可。
由于x2-x1为偶数,所以我们可以在图中圈定一个范围,计算范围内的小六边形个数,我们从样例分析,首先从列来看,总共有5列,而其中有3列为较长的列,2列为较短的列,较长的列有3个小六边形,较短的列有2个。所以呢,我们可以令x=(x2-x1)/2,y=(y2-y1)/2,那么有x+1列较长,有y+1个六边形,有x列较短,有y个六边形,所以总的被涂上色的六边形就有(x+1)*(y+1) + x*y
完整代码实现:
#include
typedef long long ll;
int main()
{
ll x1,y1,x2,y2;
while(scanf("%I64d%I64d%I64d%I64d",&x1,&y1,&x2,&y2)==4)
{
ll x=(x2-x1)/2,y=(y2-y1)/2;
printf("%I64d\n",(x+1)*(y+1)+x*y);
}
return 0;
}
F题题目链接
题目描述:
开学了去搬书
新学期到了(寒假这么快就跟我分手了)
这天,班长要叫班上的同学去搬书,所以决定成立搬书小组
每个小组人数为5-7人,而班上总共有N位同学,班长想知道总共可以分出多少个不同的小组?(存在一个组员不同或者人数不同则视为不同的小组)
输入只有一行,包含一个整数n (7 ≤ n ≤ 777).
输出一个整数,表示小组总数
7
29即C(7,5) + C(7,6) + C(7,7) = 29 C为组合符号
这道题是非常明显的组合题,从输出样例可以看出来,最后的结果应该表示为:
C(N,5) + C(N,6) + C(N,7) = (N - 4) * (N - 3) * (N - 2) * (N-1) * N / 5! +(N - 5 ) * (N - 4) * (N - 3) * (N - 2) * (N-1) * N / 6! + (N - 6) *(N - 5 ) * (N - 4) * (N - 3) * (N - 2) * (N-1) * N / 7!
但是这道题同样我们要注意一下N的取值范围,N最大值为777
那么当N取最大值时,组合数的总和为:C(777,5) + C(777,6) + C(777,7) = 777*776*775*774*773 / 5! + 777*776*775*774*773*772 / 6! +777*776*775*774*773*772*771 / 7!;
一开始我们想到这样的话就直接代入程序中计算不就好了? 可是提交后却得到wrong answer的回复。那么这是为什么呢?
首先我们来看看组合数中最大的乘积是多少,很明显,是第三个表达式,然后我们计算得:
777*776*775*774*773*772*771 = 166408909858548907200,约为1.6*10^20次方,而作为整型数据,数据范围最大的类型便是unsigned long long了,而unsigned long long的最大值为18446744073709551615,约为1.8*10^19次方,很明显,数据溢出,所以才会得到wrong answer的回复。
那么我们肯定会想,那要怎么样才能使其数据不溢出呢?
要是结果不溢出的话,我们很自然的能够想到在中间过程中将其乘积的值减小,我们看到完整表达式为777*776*775*774*773*772*771 / 7!,而又已知连续两个整数中必然有一个数对2取余为0,连续三个整数中必然有一个数对3取余为0...以此类推,那么表达式
(N - 6) *(N - 5 ) * (N - 4) * (N - 3) * (N - 2) * (N-1) * N / 7!可以写成(N - 6) *(N - 5 ) / 2 * (N - 4)/3 * (N - 3)/4 * (N - 2)/5 * (N-1)/6 * N/7,另外两个表达式与此类似,这样的话,才能保证结果不溢出。
完整代码实现:
#include
#include
typedef unsigned long long ull;
int main()
{
ull n;
while(scanf("%I64u",&n)==1&&n)
{
ull ans = 0;
ans += (n-4)*(n-3)/2*(n-2)/3*(n-1)/4*n/5 + (n-5)*(n-4)/2*(n-3)/3*(n-2)/4*(n-1)/5*n/6 + (n-6)*(n-5)/2*(n-4)/3*(n-3)/4*(n-2)/5*(n-1)/6*n/7;
printf("%I64u\n",ans);
}
return 0;
}
G题题目链接
题目描述:
这道题是线性代数
1/1 1/2 1/3
1/2 1/1 1/2
1/3 1/2 1/1
矩阵对角线上的元素始终是1/1,对角线两边分数的分母逐个递增。
请求出这个矩阵的总和。
1 2 3 4 0
1.00 3.00 5.67 8.83
很明显,这是一个对称矩阵,我们只需要计算对称矩阵对角线一边的值,然后再乘以2,结果再加上对角线的值就行了。
完整代码实现:
#include
#include
int main()
{
int N;
while(scanf("%d",&N)==1&&N)
{
double ans = 0;
for(int i = 1;i < N;++i)
ans += 2*(N-i)*(double)1/(i+1);
printf("%.2f\n",ans+N);
}
return 0;
}
H题题目链接
其实这道题才是一血
输入包含多组测试数据;
输入的第一行是一个整数C,表示有C组测试数据;
接下来是C组测试数据,每组数据输入均为0,1字符串,保证串长为偶数位(串长<=50)。
每组输出占一行。
2 0110 1100
1001 1100
这道题也属于签到题类型的题目,直接一遍for循环遍历即可
完整代码实现:
#include
#include
#include
using namespace std;
char str[60];
int main()
{
int C;
scanf("%d",&C);
while(C--)
{
scanf("%s",str);
int len = strlen(str);
for(int i = 0;i < len;i+=2)
{
char temp = str[i];
str[i] = str[i+1];
str[i+1] = temp;
}
printf("%s\n",str);
}
return 0;
} I题题目链接
题目描述:
抢车位
中文版:
一个停车场拥有(2n - 2)个空车位. 不幸的是,汽车的总数大于停车场的空车位数量. 而且,每一种类型的车的数量也超过了停车位的数量!这就是停车场上没有自由空间的原因。
在这一行摆放汽车的直线上,相同种类的汽车是连续摆放在一起的。
英文版:
To quickly hire highly skilled specialists one of the new IT City companies made an unprecedented move. Every employee was granted a car, and an employee can choose one of four different car makes.
The parking lot before the office consists of one line of (2n - 2) parking spaces. Unfortunately the total number of cars is greater than the parking lot capacity. Furthermore even amount of cars of each make is greater than the amount of parking spaces! That's why there are no free spaces on the parking lot ever.
Looking on the straight line of cars the company CEO thought that parking lot would be more beautiful if it contained exactly nsuccessive cars of the same make. Help the CEO determine the number of ways to fill the parking lot this way.
中文版:
输入只有一行,包含一个整数n (3 ≤ n ≤ 30) — 表示相同种类的车连续的数量
英文版:
The only line of the input contains one integer n (3 ≤ n ≤ 30) — the amount of successive cars of the same make.
中文版:
输出一个整数 — 总共有多少种摆放四种类型的车的方法。
英文版:
Output one integer — the number of ways to fill the parking lot by cars of four makes using the described way.
3
24
Let's denote car makes in the following way: A — 阿斯顿马丁, B — 宾利, M — 奔驰迈巴赫, Z — 扎波罗热人牌汽车. For n = 3 there are the following appropriate ways to fill the parking lot: AAAB AAAM AAAZ ABBB AMMM AZZZ BBBA BBBM BBBZ BAAA BMMM BZZZ MMMA MMMB MMMZ MAAA MBBB MZZZ ZZZA ZZZB ZZZM ZAAA ZBBB ZMMM
Originally it was planned to grant sport cars of Ferrari, Lamborghini, Maserati and Bugatti makes but this idea was renounced because it is impossible to drive these cars having small road clearance on the worn-down roads of IT City.
题意:
一公司奖励员工4种不同的汽车,而公司的停车场只有2n-2个停车位,所以停车场停不下所有车,甚至连一种车都停不完(意思是说每种汽车的数量都大于停车场停车位的数量),而老板觉得如果停车场恰有n辆相同的车排在一起会很好看,问有多少种停车方案 ?
解析:
这道题其实也不难,这是简单的排列组合的题目,但是由于题意确实叙述的有点问题,所以才导致很少人做出来的情况。
我们可以分两种情况进行讨论:
1.这n辆汽车恰好在直线两端,那么这种情况下,停车方案的总数为:4*3*4^((2n-2)-(n+1)),由于是左右两边,所以呢,计算的结果还要乘以2.即在该种情况下总的停车方案数为:24*4^(n-3)
2.这n辆汽车不在直线两端,那么这种情况下,停车方案的总数为:4*3*3*4^((2n-2)-(n+2)),而中间位置总共有(n-3)种选择,所以呢,在该种情况下总的停车方案数为:36*(n-3)* 4 ^(n-4)
然后两者相加即可(由于幂计算结果比较大,所以同时需要注意一下,数据溢出的问题)
合并为:3*(3n-1)*4^(n-3)
代入最大数据30,得出结果4809844402031689728,没有溢出long long的数据范围,因此可直接输出即可
完整代码实现:
#include
#include
typedef long long ll;
int main()
{
ll n;
while(scanf("%I64d",&n)==1&&n)
{
printf("%I64d\n",ll(pow(4,(n-3)))*(3*n-1)*3);
}
return 0;
}
总结(上):做水题的时候要注意题设的条件,以及给定数据的范围等等细节问题。