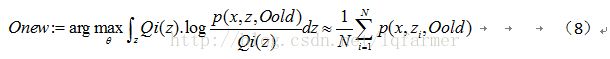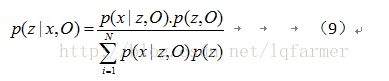Variational AutoEncoder_VAE基础：LVM、MAP、EM、MCMC、Variational Inference（VI）

Kingma et al和Rezende et al在2013年提出了变分自动编码器（Variational AutoEncoders，VAEs）模型，仅仅三年的时间，VAEs就成为一种最流行的生成模型（Generative model），通过无监督的方式学习复杂的分布。VAE和GAN一样是一种学习生成模型学习框架，它由encoder和decoder两个部分组成，两个部分都可以由CNN、LSTM、DNN等网络组成，采用梯度下降法学习网络参数。VAE是一种生成模型（Generative model），首先就从生成模型谈起。

生成模型是机器学习里一个比较广泛的概念，假设模型的观测样本为X，生成模型直接对观测样本X建模、或是基于隐变量Z的条件P（X|Z）建模。假设观测变量X的真实分布Pr（X）复杂且未知，生成模型的目的是希望通过采样的方式来建立一个模型P，目标函数是使得模型建模分布Pm（X）尽可能的去逼近观测变量X的真实分布Pr（X）。训练生成模型并不容易，存在三个问题：

1、对于观测样本X有非常强的假设。

2、常常有一些极端的近似，导致最终得到suboptimal的模型。

3、模型参数的推理往往依赖于复杂非变分MCMC方法，计算量大，实际中不可行。

针对这些问题，基于神经网络，采用反向传播方法的VAEs很好的解决了这些问题：

1、VAEs假设（assumption）很弱（weak），可以通过反向传播法快速训练模型参数。

2、VAEs采用approximation引入的误差（error）非常小，使模型具有很强的建模能力。这些优点也是VAEs快速流行的原因。

与传统的自动编码器AE，比如稀疏自动编码器和降噪自动编码器，相比，VAEs核心技巧是变分推理（variational inference）和参数重写（reparameterization）技术，其背景知识设计到了图模型和概率论中很多知识：隐变量模型（latent variable models）、最大似然估计（MLE）、最大化后验概率（MAP）、期望最大值算法（EM）、马尔科夫蒙特卡罗方法（MCMC）、KL散度（KL divergence）、变分推理（Variational Inference）相关知识。首先介绍一下相关基础知识，然后再介绍VAE模型。

1、VAEs背景知识介绍

1.1 隐变量模型（latent variable models）

在生成模型中，可观测到的样本X的真实分布是未知的。为了求解X的分布，假设存在一个由参数O确定的隐变量Z，假设Z服从参数为O的高斯分布N(0,I),由Z可以确定观测样本X的分布，Z和X关系可以用图1所示的有向图表示。

 

图1 隐变量Z和观测样本X关系示意图

结合图1和贝叶斯公式可以得到观测样本的边缘分布p（x）与隐变量z的关系：

其中，O表示参数的集合（一般参数集合用theta表示，这里为了表示输入方便，采用O表示），p（x）表示观测样本x的分布，p（x，z）表示观测样本x与隐变量z的联合概率分布，p（x|z）表示x相对于z的条件概率（隐变量z关于x的似然函数），p（z）表示隐变量z的概率分布（隐变量z先验概率），p（z|x）表示z关于x的后验概率。公式（1）相等是因为，右边通过对变量z的积分，积掉z的影响：

隐变量模型是如何工作的：隐变量z是我们制定的，这里选择假设z服从高斯分布，因此，先验概率p（z）的表达式是已知的。此外，建立由参数O确定的似然函数p（x|z）的表达式，通过极大化似然函数方法求解参数O的值，得到p（x|z）的表达式。通过公式（1），由p（z）和p（x|z）可以确定p（x）的表达式，把求解观测样本p（x）分布的问题转换为求解参数化的似然函数p（x|z）的问题。在VAE中，采用深度学习模型来表示图1中的有向图模型，刻画观测样本X的分布，通过求解深度学习模型参数来逼近真实观测样本X的分布p（x）。

在机器学习模型中，显示或者隐式的对p（z）和p（x|z）建模的模型，称为生成模型。工作时，首先依概率生成隐变量Zi ~ p（Z），在依概率通过采样得到Xi ~ p（Xi|Zi）。

 

1.2 最大似然估计（Maximum Likelihood Estimation，MLE）与最大化后验概率（MAP）

概率论里参数估计最经典的方法就是极大似然估计。给定一组观测样本X=（x1，x2....xn）,观测样本X的似然（出现的概率）定义为，注意这里的似然与上文提到的似然函数不同：

为了计算和求解方便，一般选择取似然的对数：

这样做主要目的是为了计算方便：

1、把累乘的问题转换为累加求和形式，分成多个term分别求解；

2、log对数满足Jassen不等式，方便采用EM等优化算法求解；

3、求导方便，降低数量级。

极大似然估计求解时认为模型的参数O是确定的，一定存在一个最优的参数O*使得似然函数最大化，参数估计的问题就转换成最大化对数似然函数的问题。

与极大似然估计观点相对的是贝叶斯学派观点，即最大化后验概率（Maximum A Posterior，MAP）。贝叶斯学派认为，模型的参数O是一个随机变量，其服从分布p（O）。

MAP优化的目标函数如公式（4）所示。

 

1.3 期望最大值算法（Expectation Maximization，EM）

在隐变量模型中，通过推导得出了：求解观测样本p（X）的分布的问题转化成求解联合概率p（x，z）对数形式，如公式（5）：

因此，在得到p（z）和p（X|z）表达式的情况下，采用深度学习模型对p（X|Z）建模，可以通过期望最大值算法（EM）求解模型参数O。

随机初始化模型参数Oold。

E-step：根据参数初始值或上一次迭代的模型参数来计算隐变量z的后验概率p（z|x，Oold），做为隐变量z的概率值的估计：

M-step：将似然函数最大值以获得新的参数值：

通过不断地迭代，收敛于最终的参数O*。EM算法典型的应用是用于解决高斯混合模型（Gaussian Mixtrue Model，GMM）的参数估计问题。EM算法是变分推理的基础，关于EM算法的收敛性证明和更多介绍请看PRML中8-11章。

 

1.4 马尔科夫蒙特卡罗方法（MCMC）

EM算法在最大化似然函数的过程中涉及对后验概率p（z|x，O）的积分，当求解高纬度或者复杂的分布时候，直接计算后验概率的积分是不可行的。因此，只有通过采样的方法近似的求解似然函数的值。

按照条件概率p（z|x）对z进行采样。采用MCMC的方法进行采样，典型的MCMC方法有Metropolis Hastings，MH算法和Gibbs算法，Gibbs算法是MH算法特例。

 

1.5 KL散度（KL divergence）与变分推理（Variational Inference）

通过MCMC采样来近似计算后验概率存在一个问题：MCMC需要对每个数据点采样，计算量非常大，当处理大数据量时，直接计算不可行。

后验概率的分母为归一化因子，当数据量大时，直接计算归一化因子是不可行的。因此采用变分推理方法求解参数O。变分推理时，对观测样本X的对数似然做如下变换：

在公式（10）中，KL（q||p）表示分布q与分布p之间的散度，（Kullback-Leibler divergence）KL散度用于衡量两个分布之间的距离，L(q)表示的是变分的证据下界目标函数（Evidence Lower Bound Objective，ELBO）。变分就是插入一个分布q（Z|X）到求解观测变量X的分布的表达式中，用一个简单的分布q(Z|X)来近似比较复杂的后验分布p（Z|X）。


KL距离恒>=0，当且仅当分布q和p完全相同时，即p=q时，KL（q||p）=0，注意KL（q||p）不等于KL（p||q）。我们的直接目标是argmin（KL（q||p）），但因为KL（q||p）同样设计求解后验概率p（Z|X），不能直接求解。问题可以转换为最大化变分的ELBO函数L（q），假设观测变量X的分布p（X）是不变的，最大化ELBO同时，也等价于最下化KL（q||p）。

与KL（q||p）相比，以ELBO函数作为目标函数来求解参数O的值方便很多，因为ELBO设计的联合概率p（X，Z）和后验概率q（Z|X）容易计算：p（X，Z）在EM算法中给出了计算公式，q（Z|X）使我们自己构造的。

关于EM算法、MCMC和Variational inference的详细知识，参考徐亦达老师的视频教程和PRML教材的8-11章。

参考资料
Variational Auto-Encoders
Tutorial on Variational Autoencoders
Grammar Variational Autoencoder
PRML：8-11章

更多深度学习在NLP方面应用的经典论文、实践经验和最新消息，欢迎关注微信公众号“深度学习与NLP”或“DeepLearning_NLP”或扫描二维码添加关注。