面试题——查找字符串中最长的回文子串
给定一个字符串 s,找到 s 中最长的回文子串。
暴力法一 O(n^3)
使用临时变量保存当前查找到的最长回文子串,通过两层循环找出字符串的所有子串,对每一个子串进行回文判断,当是判断的子串是回文时,对比先前保存的最长的回文子串和当前回文子串的长度;用较长的串替换当前串, 如果两串长度相同,则不更改。
public static String findLongestHuiWen1(String s){
if(s==null || s.length()<=1) return s;
int maxLen = 0;
String maxStr = "";
for(int i=0; imaxLen){
maxLen = subString.length();
maxStr = subString;
}
}
}
return maxStr;
}
public static boolean isHuiWen(String s){
if(s==null || s.length()==0) return false;
char[] arr = s.toCharArray();
int left = 0;
int right = arr.length-1;
while (left 暴力法二 O(n^3)
使用临时变量保存当前查找到的最长回文子串的起始和结束位置,通过两层循环找出字符串的所有子串,对每一个子串从始末位置往中心进行回文判断,若满足回文条件,判断该串的长度是否更大,若更大,则更新最长回文子串的起始和结束位置。
public static String findLongestHuiWen2(String s){
if(s==null || s.length()<=1) return s;
int begin = 0; //子串的开始位置
int end = 0; //子串的结束位置
for(int i=0; i=right && j-i > end-begin){
begin = i;
end = j;
}
}
}
return s.substring(begin, end+1);
}
中心拓展法一O(n^2)
使用临时变量保存当前查找到的最长回文子串,选择一个字符作为中心,向两边查找回文串。
1、遍历一遍字符串(从index = 1开始遍历),以下标为中心,考虑子串长度是奇数或偶数,在这两种情况下拓展子串,判断子串是否是回文串。
2、奇数子串,对比字符的前一个和后一个 i-1 和 i+1,进行判断,并比较长度。
3、偶数子串,对比字符的前一个和当前字符 i 和 i-1,进行判断,并比较长度。
4、更新保存的最长回文字符串。
public static String findLongestHuiWen4(String s){
if(s==null || s.length()<=1) return s;
String maxStr = "";
int maxLen,left,right;
for(int i=1; i=0 && right maxStr.length()){
maxStr = s.substring(left+1, right);
}
//偶数子串
maxLen=0;
for (left=i-1,right=i; left>=0 && right maxStr.length()){
maxStr = s.substring(left+1, right);
}
}
return maxStr;
}
中心拓展法二O(n^2)
使用临时变量保存当前查找到的最长回文子串的起始和结束位置,选择一个字符作为中心,向两边查找回文串。
1、遍历一遍字符串(从index = 1开始遍历),以下标为中心,考虑子串长度是奇数或偶数,在这两种情况下拓展子串,判断子串是否是回文串。
2、奇数子串,对比字符的前一个和后一个 i-1 和 i+1,进行判断,并比较长度。
3、偶数子串,对比字符的前一个和当前字符 i 和 i-1,进行判断,并比较长度。
4、更新保存的起始和结束位置。
public static String findLongestHuiWen3(String s){
if(s==null || s.length()<=1) return s;
int begin = 0;
int end = 0;
//从第二个字符开始遍历
for(int i=1; i=0 && right<=s.length()-1 && s.charAt(left)==s.charAt(right)){
left--;
right++;
}
if((right-1)-(left+1) > end-begin){
begin = left+1;
end = right-1;
}
//偶数子串
left = i-1;
right = i;
while(left>=0 && right<=s.length()-1 && s.charAt(left)==s.charAt(right)){
left--;
right++;
}
if((right-1)-(left+1) > end-begin){
begin = left+1;
end = right-1;
}
}
return s.substring(begin, end+1);
}
Manacher算法(马拉车算法)O(n)
这个算法的总框架是,遍历所有的中心点,寻找每个中心点对应的最长回文子串,然后找到所有中心点对应的最长回文子串,与中心拓展法思想类似,但而马拉车算法对其进行了改进,将复杂度变为了线性。
1、在字符间插入特殊字符
由于回文串的长度可奇可偶,比如"bob"是奇数形式的回文,"noon"就是偶数形式的回文,马拉车算法的第一步是预处理,做法是在每一个字符的左右都加上一个特殊字符,比如加上’#’,那么
s="google"
->
ss="#g#o#o#g#l#e#"
这样做的好处是不论原字符串是奇数还是偶数个,处理之后得到的字符串的个数都是奇数个,这样,循环时便不用考虑原字符串长度的奇偶性了。
2、计算半径数组p
该数组的长度与处理后的字符串 ss 等长,其中 p[i] 表示以 ss[i] 为中心的最长回文子串的半径,暂且把它称为半径数组。如果 p[i] = 1,则说明回文子串就是 ss[i] 本身。比如,"#a#b#"的半径数组为[1,2,1,2,1]。
为了在搜索回文子串时避免总是判断是否越界,我们在 ss 的首尾两端加上两个不同的特殊字符,保证这两个特殊字符不会出现在 ss 中。比如为 $ 和 ^。则 ss 变为了
ss = "$#g#o#o#g#l#e#^"
通过 p 数组我们就可以找到其最大值和其位置,就能确定最长回文子串。
如何计算数组 p
一般的方法,是以中心点为中心,挨个将半径逐步扩张,直至字符串不再是回文字符串。但是这样做,整体的算法复杂度为 O(n2)。马拉车算法的关键之处,就在于巧妙的应用了回文字符串的性质,来计算数组 p。
马拉车算法在计算数组 p 的整个流程中,一直在更新两个辅助变量:
mx:已找到的回文子串所能达到的最右端的位置
id:最右端回文子串的对应的中心位置
使用这两个变量,便可以用一次扫描来计算出整个数组 p,这个算法的最核心的一行如下:
p[i] = mx > i ? Math.min( p[2 * id - i], mx - i) : 1;
这行代码拆开来看就是,
如果mx > i,则 p[i] = min(p[2 * id - i], mx - i)
否则, p[i] = 1
当 mx - i > P[j] 的时候,以S[j]为中心的回文子串包含在以S[id]为中心的回文子串中,由于 i 和 j 对称,以S[i]为中心的回文子串必然包含在以S[id]为中心的回文子串中,所以必有 P[i] = P[j],见下图。
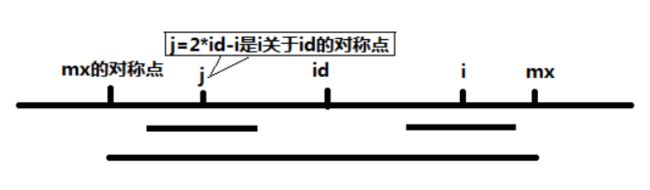
当 P[j] >= mx - i 的时候,以S[j]为中心的回文子串不一定完全包含于以S[id]为中心的回文子串中,但是基于对称性可知,下图中两个绿框所包围的部分是相同的,也就是说以S[i]为中心的回文子串,其向右至少会扩张到mx的位置,也就是说 P[i] >= mx - i。至于mx之后的部分是否对称,就只能老老实实去匹配了。
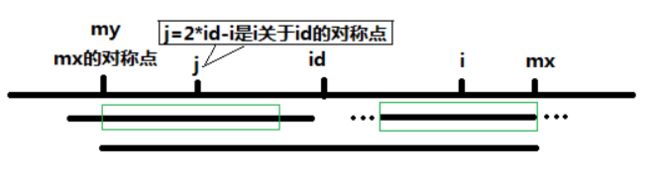
对于 mx <= i 的情况,无法对 P[i]做更多的假设,只能P[i] = 1,然后再去匹配了。
3、数组 p 中的最大值,即为最长回文子串的半径
在改变后字符串的最大回文中心位置和半径长度转化为原字符串中的起始点下标。
cabccbaa
01234567
->
$ # c # a # b # c # c # b # a # a # ^
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
已知:centerIndex=9,ansLen=7
计算原始末位置下标
int begin =(centerIndex-ansLen)/2 ;
int end = (centerIndex+ansLen)/2-1;
public static String findLongestHuiWen5(String s){
if(s==null || s.length()<=1) return s;
//插入特殊字符,且奇数
StringBuilder sb = new StringBuilder("$#");
for(int i=1; ii:当前求解位置在已经能够达到的位置之内
p[i] = mx > i ? Math.min( p[2*id-i], mx-i) : 1;
//在已有回文串的基础上求解一个最大回文串
while((i-p[i]>=0) && (i+p[i]mx){
mx = i+p[i];//可以到达为止的下一位置
id = i; //对应的中心点
}
//当前求解的最大回文串和存储中的最大回文串
if(ansLen