网易 | 数据结构和算法 | 学习笔记03：树

视频课程：数据结构（浙江大学： 陈越、何钦铭）（第三讲、第四讲）

┏━━━━━━目录━━━━━━┓

3.1 树与树的表示

3.2 二叉树及存储结构

3.3 二叉树的遍历

4.1 二叉搜索树

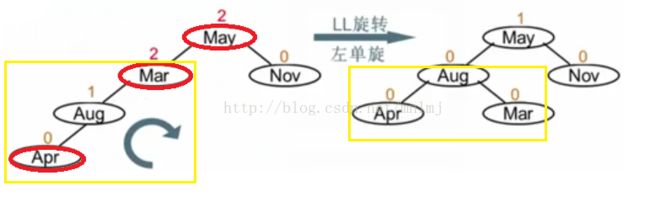
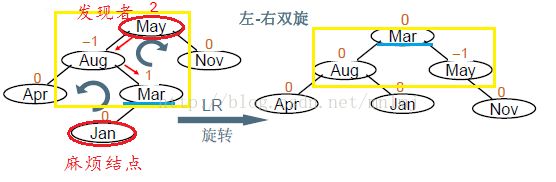
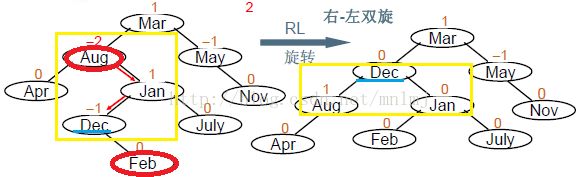
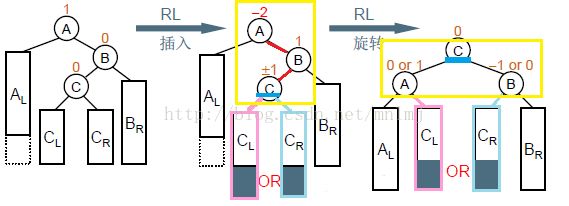
4.2 平衡二叉树

4.3 堆

4.4 哈夫曼树与哈夫曼编码

4.5 集合及运算

┗━━━━━━━━━━━━━━┛

3.1 树与树的表示

（层次关系：分层次组织在管理上具有更高的效率）

1、引子：查找——根据某个给定关键字K ，从集合R中找出关键字与K相同的记录

（1）静态查找：集合中记录是固定的——没有插入和删除操作，只有查找

〖方法1〗顺序查找：时间复杂度为O(n)

* 算法技巧：建立哨兵

〖方法2〗二分查找（Binary Search)：时间复杂度O(logN)  

[注]：为什么是logN？因为每次查找范围除以2，一直除到1

① 假设n个数据元素的关键字满足有序（比如：小到大）

② 并且是连续存放（数组），那么可以进行二分查找。

* left > right ? 查找失败，结束

* 二分查找判定树

（以11个元素为例）

① 判定树上每个结点需要的查找次数刚好为该结点所在的层数;
② 查找成功时查找次数不会超过判定树的深度

（查找效率是树的高度）

 n个结点的判定树的深度为：[log(2,n)]+1.【以2为底n的对数,取整+1】

平均成功查找次数 ASL = (4*4+4*3+2*2+1)/11 = 3

（2）动态查找：集合中记录是动态变化的—— 除查找，还可能发生插入和删除

【见4.1二叉搜索树】

3、 树的定义

（1）树（Tree）: n（n≥0）个结点构成的有限集合。

（2）当n=0时，称为 空树；
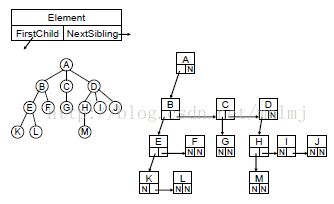
（3）对于任一棵非空树（n> 0），它具备以下性质：
① 树中有一个称为“ 根（Root）”的特殊结点，用 r 表示；
② 其余结点可分为m(m>0)个 互不相交的有限集T1，T2，... ，Tm，其中每个集合本身又是一棵树，称为原来树的“ 子树（SubTree）”

（4）注意：

① 子树是 不相交的；
②  除了根结点外， 每个结点有且仅有一个父结点；
③ 一棵N个结点的树有 N-1条边。

（5）树的一些基本术语

1.结点的度（Degree）：结点的子树个数
2.树的度：树的所有结点中最大的度数
3.叶结点（Leaf）：度为0的结点
4.父结点（Parent）：有子树的结点是其子树的根结点的父结点
5.子结点（Child）：若A结点是B结点的父结点，则称B结点是A结点的子结点；子结点也称孩子结点。
6.兄弟结点（Sibling）：具有同一父结点的各结点彼此是兄弟结点。

7.路径和路径长度：从结点n1到nk的路径为一个结点序列n1 , n2 ,… , nk , ni是 ni+1的父结点。路径所包含边的个数为路径的长度。

9. 祖先结点(Ancestor)：沿树根到某一结点路径上的所有结点都是这个结点的祖先结点。 

10. 子孙结点(Descendant)：某一结点的子树中的所有结点是这个结点的子孙。 

11. 结点的层次（Level）：规定根结点在1层，其它任一结点的层数是其父结点的层数加1。 

12. 树的深度（Depth）：树中所有结点中的最大层次是这棵树的深度。

4、 树的表示：儿子-兄弟表示法

（1）n个节点，n-1条边，指针域2n，空指针2n-(n-1)=n+1

（2）将这棵树旋转45°得到一颗二叉树

3.2 二叉树及存储结构

1、 二叉树的定义：一个有穷的结点集合。

（1）这个集合可以为空
（2）若不为空，则它是由 根结点和称为其 左子树TL和 右子树TR的两个不相交的二叉树组成。
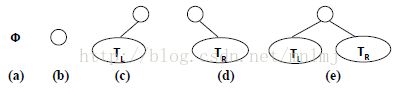
（3）二叉树具体五种基本形态（空树、只有一个结点、左子树非空、右子树非空、都非空）

（4）与度为2的一般树的区别为：二叉树的子树有左右顺序之分（见上图cd，是不同的情况）

2、 特殊二叉树

（1）斜二叉树(Skewed Binary Tree)——线性结构 

（2）完美二叉树(Perfect Binary Tree) 满二叉树(Full Binary Tree）

（3） 完全二叉树 (Complete Binary Tree) 有n个结点的二叉树，对树中结点按从上至下、从左到右顺序进行编号，编号为i（1 ≤ i ≤ n）结点与满二叉树中编号为 i 结点在二叉树中位置相同｛tip：只能缺右下那一块儿叶结点｝

（斜二叉树，完美二叉树）

3、二叉树几个重要性质

（1）一个二叉树第 i 层的最大结点数为：2^( i-1)，i ≥ 1。  ——2、4、8、16……

（2）深度为k的二叉树有最大结点总数为：2^k -1，k ≥ 1。——对(1)求和
（3）对任何非空二叉树 T，若n0表示叶结点的个数、n2是度为2的非叶结点个数，那么两者满足关系n0 = n2 +1。

〖证明〗

边的总数=n0+n1+n2-1 （向上看：每个结点都有一条边，唯一的根结点向上没有边）

                =0*n0+1*n1+2*n2 （向下看：叶结点没有边，度为1的结点1条边，度为2的结点两条边）

化简后得n0 = n2 +1，证毕。

4、 二叉树的抽象数据类型定义

（1）类型名称：二叉树
（2）数据对象集：一个有穷的结点集合。若不为空，则由根结点和其左、右二叉子树组成。
（3）操作集： BT BinTree, Item  ElementType，重要操作有：
①Boolean IsEmpty( BinTree BT )： 判别BT是否为空；
②void Traversal( BinTree BT )： 遍历，按某顺序访问每个结点；
③BinTree CreatBinTree( )：创建一个二叉树。

（4）常用的遍历方法有：
①void PreOrderTraversal( BinTree BT )： 先序----根、左子树、右子树；
②void InOrderTraversal( BinTree BT )： 中序---左子树、根、右子树；
③void PostOrderTraversal( BinTree BT )：后序---左子树、右子树、根
④void LevelOrderTraversal( BinTree BT )：层次遍历，从上到下、从左到右

5、 二叉树的存储结构

（1） 顺序存储结构

● 完全二叉树：按从上至下、从左到右顺序存储n个结点的完全二叉树的结点父子关系：

①非根结点（序号 i > 1）的 父结点的序号是  i / 2 ;
②结点（序号为 i ）的左孩子结点的序号是 2i， （若2 i <= n，否则没有左孩子）;
③结点（序号为 i ）的右孩子结点的序号是 2i+1， （若2 i +1<= n，否则没有右孩子）;

● 一般二叉树：补充为对应的完全二叉树，也可以采用这种结构，但会造成空间浪费

（2） 链表存储：data、left、right

3.3 二叉树的遍历

* 二叉树的遍历很重要，之后对二叉树的操作，都可以根据遍历修改实现。

1、二叉树的 递归遍历——（先序、中序和后序）堆栈实现

（1）先序遍历
①访问根结点；
②先序遍历其左子树；（递归）
③先序遍历其右子树。（递归）

〖例〗先序遍历=> A（B D F E ）（C G H I）

（2）中序遍历

①中序遍历其左子树；（递归）
②访问根结点；
③中序遍历其右子树。（递归）

〖例〗中序遍历=>（D B E F） A （G H C I）

（3）后序遍历

①后序遍历其左子树；（递归）
②后序遍历其右子树；（递归）
③访问根结点。

〖例〗后序遍历=>（D E F B ）（ H G I C） A

* 先序、中序和后序遍历过程： 遍历过程中经过结点的路线一样，只是访问各结点的时机不同。

* 图中在从入口到出口的曲线上用叉、星和三角三种符号分别标记出了先序、中序和后序访问各结点的时刻

2、二叉树的非递归遍历

* 非递归算法实现的基本思路：使用堆栈

（1）中序遍历 非递归遍历算法
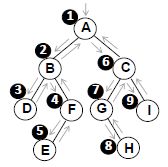
①遇到一个结点，就把它压栈，并去遍历它的左子树；
②当左子树遍历结束后，从栈顶弹出这个结点并访问它；
③ 然后按其右指针再去中序遍历该结点的右子树。

void InOrderTraversal( BinTree BT )
{ BinTree T=BT;
  Stack S = CreatStack( MaxSize ); /*创建并初始化堆栈S*/
  while( T || !IsEmpty(S) ){
      while(T){                    /*一直向左并将沿途结点压入堆栈*/
          Push(S,T);
          T = T->Left;
      }
      if(!IsEmpty(S)){
          T = Pop(S);               /*结点弹出堆栈*/
          printf(“%5d”, T->Data); /*（访问）打印结点*/
          T = T->Right;             /*转向右子树*/
      }
  }
}

（2）先序遍历的非递归遍历算法：更换“（访问）打印结点”的位置

3、 层序遍历——队列实现
（1）二叉树遍历的核心问题：二维结构的线性化
<Ⅰ> .从结点访问其左、右儿子结点
<Ⅱ>访问左儿子后，右儿子结点怎么办？
      ① 需要一个存储结构保存暂时不访问的结点
      ② 存储结构：堆栈、队列

（2）  队列实现：遍历从根结点开始，首先将根结点入队，然后开始执行循环：结点出队、访问该结点、其左右儿子入队

｛注：根节点进入队列；loop { 出队、出队元素的左右儿子入队}｝

〖例〗层序遍历 => ABCDFGIEH

（3）层序基本过程：先根结点入队，然后：

① 从队列中取出一个元素；

②访问该元素所指结点；
③若该元素所指结点的左、右孩子结点非空， 则将其左、右孩子的指针顺序入队。

4、遍历应用例子

（1）输出二叉树中的叶子结点。

〖分析〗在二叉树的遍历算法中增加检测结点的“左右子树是否都为空”。（可在先序遍历的print之前增加if语句）

（2）求二叉树的高度。

〖分析〗Height=max(HL, HR)+1（利用后序遍历的框架，递归的求取）

（3）二元运算表达式树及其遍历

〖分析〗三种遍历可以得到三种不同的访问结果：
①先序遍历得到前缀表达式：+ + a * b c * + * d e f g
②中序遍历得到中缀表达式：a + b * c + d * e + f * g

（中缀表达式会受到运算符优先级的影响，可能会发生错误；输出左子树之前加个左括号，结束时加个右括号，可更正）
③后序遍历得到后缀表达式：a b c * + d e * f + g * +

（4） 由两种遍历序列确定二叉树

〖分析〗已知三种遍历中的任意两种遍历序列，能否唯一确定一棵二叉树呢？

〖答案〗 必须要有中序遍历才行。否则，根容易确定，但是左右的边界无法确定。

<Ⅰ>先序和中序遍历序列来确定一棵二叉树
〖分析〗
①根据 先序遍历序列第一个结点确定 根结点；
②根据根结点在 中序遍历序列中 分割出左右两个子序列
③对左子树和右子树分别 递归使用相同的方法继续分解。

〖例〗由先序和中序遍历序列来画出一棵二叉树

先序序列：a b c d e f g h i j
中序序列：c b e d a h g i j f

<Ⅱ>类似地，后序和中序遍历序列也可以确定一棵二叉树。

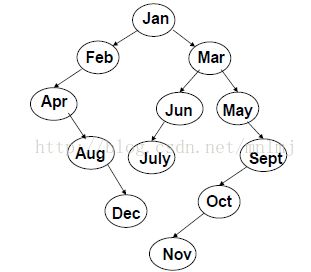
4.1 二叉搜索树（BST，Binary Search Tree）

1、定义

（1）二叉搜索树也称二叉排序树或二叉查找树

（2）二叉搜索树：一棵二叉树，可以为空；如果不为空，满足以下性质：
① 非空 左子树的所有键值 小于其根结点的键值。
② 非空 右子树的所有键值 大于其根结点的键值。
③ 左、右子树都是二叉搜索树。

2、二叉搜索树操作的特别函数

①Position Find( ElementType X, BinTree BST )：从二叉搜索树BST中 查找元素X，返回其所在结点的地址；
②Position FindMin( BinTree BST )：从二叉搜索树BST中查找并返回 最小元素所在结点的地址；
③Position FindMax( BinTree BST ) ：从二叉搜索树BST中查找并返回 最大元素所在结点的地址。
④BinTree Insert( ElementType X, BinTree BST )  插入
⑤BinTree Delete( ElementType X, BinTree BST ) 删除

（1）二叉搜索树的 查找操作：Find—— 查找的效率决定于树的高度
①查找从根结点开始，如果树为空，返回NULL
②若搜索树非空，则根结点关键字和X进行比较，并进行不同处理：
③若X小于根结点键值，只需在左子树中继续搜索；
④如果X大于根结点的键值，在右子树中进行继续搜索；
⑤若两者比较结果是相等，搜索完成，返回指向此结点的指针。

（2）查找 最大和最小元素
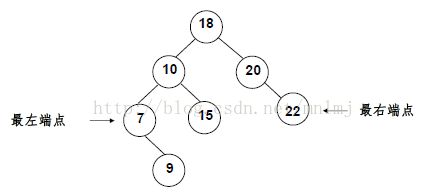
①最大元素一定是在树的最右分枝的端结点上（沿着左分支，找到最后一个left）
②最小元素一定是在树的最左分枝的端结点上

（3）二叉搜索树的 插入

〖分析〗关键是要找到元素应该插入的位置，可以采用与Find类似的方法（每次进入左右分之前记住父结点的位置）

〖例〗以一年十二个月的英文缩写为键值，按从一月到十二月顺序输入，即输入序列为（Jan, Feb, Mar, Apr, May, Jun, July, Aug, Sep, Oct, Nov, Dec）

（2）二叉搜索树的 删除

〖分析〗考虑三种情况：
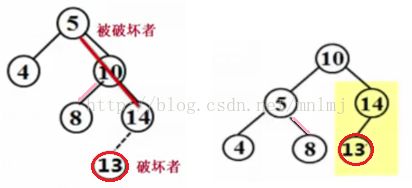
①要删除的是叶结点：直接删除，并再修改其父结点指针---置为NULL

②要删除的结点只有一个孩子结点: 将其父结点的指针指向要删除结点的孩子结点

③要删除的结点有左、右两棵子树： 用另一结点替代被删除结点：右子树的最小元素 或者 左子树的最大元素

〖注〗右子树的最小值&左子树的最大元素，一定不是有两个儿子的结点。③中把两儿子的情况转换为了①②情况。

左子树中的最大值一定是在树的最右分枝的端结点，不可能有右儿子；

右子树中的最小值一定是在树的最左分枝的端结点，不可能有左儿子。

〖例〗 删除41

4.2 平衡二叉树（Balanced Binary Tree）（AVL树）

1、定义

（1）〖例〗搜索树结点不同插入次序，将导致不同的深度和平均查找长度ASL

〖分析〗第i层有x个结点，第i层的结点需要查找x次。共有n个结点。ASL=每个结点的查找次数之和 / 总结点数

{ 越平衡，树的高度越低，搜索效率变高 }

（2）平衡因子（Balance Factor，简称BF）

BF(T) = hL-hR， 其中hL和hR分别为T的左、右子树的高度。

（3） 平衡二叉树定义：空树，或者任一结点左、右子树高度差的绝对值不超过1，即|BF(T) |≤ 1

〖例〗是否是平衡二叉树

〖分析〗（1）3结点左边高度2，右边高度0；（2）是平衡二叉树；（3）7结点左边高度3右边高度1。

2、 平衡二叉树的高度能达到log2n吗？

〖答案〗 给定结点数为 n的AVL树的最大高度为O(log2n)

〖分析1〗完全二叉树的结点高度能达到log2n

〖分析2〗设 nh 高度为h的平衡二叉树的最少结点数。结点数最少时：

①高度为边的个数，两层的高度h为1，一层的高度h为0

②高度为h时，结点数最少的两种情况：左子树高度(h-2)右子树高度(h-1)、左子树高度(h-1)右子树高度(h-2)

此时结点数为：（高度为h-1最少结点数）+（高度为h-2的最少结点数）+1个根节点

nh与斐波那契数列的关系：

3、 平衡二叉树的调整

* 四种方法如何选择： 观察插入者位置与 被破坏者位置的关系

* 查找树，必须保证 左小右大，做出相应调整。

* 注意：有时候插入元素即便不需要调整结构，也可能需要 重新计算一些平衡因子。

（1）RR 旋转

〖例〗 不平衡的“发现者”是Mar，“麻烦结点”Nov 在发现者右子树的右边，因而叫 RR 插入，需要RR 旋转（右单旋）

* 插入NOV（麻烦结点）的时候，Mar结点（发现者）不平衡，

〖分析〗

① 原本是平衡二叉树，插入x后，A结点的平衡被破坏；

② A与x是右子树右子树的关系，此时做RR旋转；

③ 被破坏的A结点的右子树拎上来作为父结点；

④ 为了满足查找树的要求，多出的结点BL（A

〖例〗插入15结点时，5被破坏，15的位置在5的右子树的右子树上，采用RR旋转。

〖例〗插入13结点时，5被破坏，13的位置在5的右子树的右子树上，依然采用RR旋转。

（2）LL  旋转

〖例〗 “发现者”是Mar，“麻烦结点”Apr 在发现者左子树的左边，因而叫 LL 插入，需要LL 旋转（左单旋）

〖分析〗插入Apr的时候，Mar、May被破坏，Apr是Mar的左结点的左结点，采用LL旋转

*  被破坏的不止一个结点(Mar、May)，调整的时候从最下面一个开始，上面的随之解决；

*  旋转不一定只发生在根节点。

（3）LR 旋转

〖例〗 “发现者”是May，“麻烦结点”Jan在左子树的右边，因而叫 LR 插入，需要LR 旋转

* 麻烦结点是发现者的左子树的右子树；

* 这三点中Mar是中间值，作为新的父节点。

〖分析〗

（4）RL 旋转

〖例〗 “发现者”是Aug，“麻烦结点”Feb在右子树的左边，因而叫 RL 插入，需要 RL 旋转

〖分析〗

4.3 堆(heap)

1、 优先队列（Priority Queue）：特殊的“队列”，取出元素的顺序是 依照元素的优先权（关键字）大小，而 不是元素进入队列的 先后顺序。

（1）若采用数组或链表实现优先队列

【数组】
插入 — 元素总是插入尾部 ~ Θ ( 1 )
删除 — 查找最大（或最小）关键字 ~ Θ ( n )
            去需要移动元素 ~ O( n )

【链表】
插入 — 元素总是插入链表的头部 ~ Θ( 1 )
删除 — 查找最大（或最小）关键字 ~ Θ( n )
            删去结点 ~ Θ( 1 )

【有序数组】
插入 — 找到合适的位置 ~ O( n ) 或 O(log2 n )
            移动元素并插入 ~ O( n )
删除 — 删去最后一个元素 ~ Θ( 1 )

【有序链表】
插入 — 找到合适的位置 ~ O( n )
            插入元素 ~ Θ( 1 )
删除 — 删除首元素或最后元素 ~ Θ( 1 )

（2）二叉树表示

〖分析〗采用二叉树存储结构？

* 若采用二叉搜索树，每次删除的时候删除最大(或最小)值，导致树不平衡，高度不再是log2n

* 在删除&插入中，删除更难做，最大值在根部更方便删除，使每个结点都比左右子树大。

● 用完全 二叉树表示优先队列——堆

<Ⅰ>两个特性

①结构性：用数组表示的完全二叉树；
②有序性：任一结点的关键字是其子树所有结点的最大值(或最小值)
——“最大堆(MaxHeap)”,也称“大顶堆”：最大值
——“最小堆(MinHeap)”,也称“小顶堆” ：最小值

〖例〗是否是堆（是完全二叉树；每一结点是子树的最大/小值）

注意：从根结点到任意结点路径上结点序列的有序性！

<Ⅱ> 堆的抽象数据类型描述

①类型名称： 最大堆（MaxHeap） 

②数据对象集：完全二叉树，每个结点的元素值不小于其子结点的元素值 

③操作集：最大堆H  MaxHeap，元素item  ElementType

④主要操作有：
•MaxHeap Create( int MaxSize )：创建一个空的最大堆。
•Boolean IsFull( MaxHeap H )：判断最大堆H是否已满。
•Insert( MaxHeap H, ElementType item )：将元素item 插入最大堆H。
•Boolean IsEmpty( MaxHeap H )：判断最大堆H是否为空。
•ElementType DeleteMax( MaxHeap H )：返回H中最大元素(高优先级)。

<Ⅲ>算法

【插入】将新增结点插入到从其父结点到根结点的有序序列中 （插入到完全二叉树的末尾，比其父结点大，则交换位置。）

（* [0]位置有一个大于所有值的“哨兵”，提高算法效率）

【删除】取出根结点（最大值）元素，同时删除堆的一个结点。（ 是队列，只能一头进入，一头删除）

①删除根节点

②把末尾元素值替补根节点（保留完全二叉树的结构特点）

③新的根节点与循环与较大的儿子交换（保证有序性，时间复杂度为树的高度）

④结点>max（左、右儿子）循环结束。

【建立】最大堆的建立：将已经存在的N个元素按最大堆的要求存放在一个一维数组中

方法1：通过插入操作，将N个元素一个个相继插入到一个初始为空的堆中去，其时间代价最大为O(N logN)。

方法2：在线性时间复杂度下建立最大堆，线性时间复杂度T(n)=O(n)
① 将N个元素按输入顺序存入，先满足完全二叉树的结构特性
② 调整各结点位置，以满足最大堆的有序特性。

〖分析〗

①从倒数第一个有儿子结点的结点开始调整，用与“删除”相似的方法，找到该节点左右儿子的最大值，交换。

（左、右边一定只有一个孩子，所以它的左右子树一定是堆）

②向前顺着调整结点（向左向上）

4.4 哈夫曼树与哈夫曼编码

* 如何根据结点不同的查找频率构造更有效的搜索树？

1、哈夫曼树的定义

带权路径长度(WPL)：设二叉树有n个叶子结点，每个叶子结点带有权值 wk，从根结点到每个叶子结点的长度为 lk；

则每个叶子结点的带权路径长度之和就是： WPL=Σ wk·Ik （k=1...n）

最优二叉树（哈夫曼树）为带权路径长度WPL值最小的二叉树

〖例〗有五个叶子结点，它们的权值为{1,2,3,4,5}，用此权值序列可以构造出形状不同的多个二叉树。

* 不同的顺序，不同的结构，得到的WPL不同。

WPL ＝ 5×1＋4×2＋3×3＋2×4＋1×4＝34
WPL ＝1×3＋2×3＋3×2＋4×2＋5×2＝33
WPL＝1×1＋2×2＋3×3＋4×4＋5×4＝50

2、 哈夫曼树的构造：每次把权值最小的两棵二叉树合并——用堆实现效率高。

* 整体复杂度为O(N logN)

〖例〗1、2、3、4、5构造哈夫曼树

①选取最小的"1"、"2"，合并权值为3；

②在合并的“3”和剩下的“3“、“4“、“5“中选取最小的“3“、“3“，合并权值为6；

③在合并的“6“和剩下的“4“、“5“中，选取最小的“4“、“5“，合并为9；

④最后只有“6“、“9“合并为15。

4、 哈夫曼树的特点:
（1）没有度为1的结点；（因为是两两合并构造的）

（2）n个叶子结点的哈夫曼树共有2n-1个结点；

* n2为有2个儿子的结点，n0是叶结点。有n2=n0-1

* 对哈夫曼树n1=0，总结点数=n2+n0=(n0-1)+n0=2n0-1

（3）哈夫曼树的任意非叶节点的左右子树交换后仍是哈夫曼树；

（4）对同一组权值{w1 ,w2 , …… , wn}，是否存在不同构的两棵哈夫曼树呢？

* 存在，但是WPL值是一致的。
* 例：对一组权值{ 1, 2 , 3, 3 }，不同构的两棵哈夫曼树：

5、哈夫曼编码

〖思考〗给定一段字符串，如何对字符进行编码，可以使得该字符串的编码存储空间最少？

〖例〗假设有一段文本，包含58个字符，并由以下7个字符构：a，e，i，s，t，空格（sp），换行（nl）；

          这7个字符出现的次数不同。如何对这7个字符进行编码，使得总编码空间最少？
〖分析〗
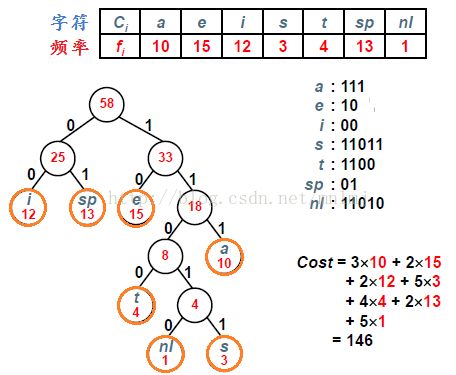
（1）用等长ASCII编码：58 ×8 = 464位；（每个ASCII码占1个字节=8bit）
（2）用等长3位编码：58 ×3 = 174位；（3位可以表示2^3=8个不同的字符）
（3）不等长编码：出现频率高的字符用的编码短些，出现频率低的字符则可以编码长些？ （见下文解答）

*  怎么进行不等长编码？如何避免二义性？

前缀码prefix code：任何字符的编码都不是另一字符编码的前缀；可以无二义地解码

* 用二叉树进行编码：
（1）左右分支：0、1
（2）字符只在叶结点上（此时不会出现一个字符的编码是另一字符编码的前缀，不会有二义性）

〖例〗四个字符的频率: a:4, u:1, x:2, z:1，比较以下两种编码，等长与非等长编码。

〖例〗 （解答上文例题）假设有一段文本，包含58个字符，并由以下7个字符构：a，e，i，s，t，空格（sp），换行（nl）；

4.5 集合及运算

1、 集合的表示

（1） 集合运算： 交、并、补、差，判定一个元素是否属于某一集合

（2） 并查集：集合并、查某元素属于什么集合
* 并查集问题中集合存储如何实现？——可以用树结构表示集合，树的每个结点代表一个集合元素

〖例〗有10台电脑{1,2,3,...,9,10}，一直下列电脑之间实现了链接：

1和2，2和4，3和5，4和7，5和8，6和9，6和10

问：2和7之间，5和9之间是富士连通的

〖分析〗

①将10台电脑看成10个集合，{1},{2},{3},...,{9},(10)；

②已知一种连接“x和y”，就将x和y对应的集合合并；

③查询“x和y是否是连通的”就是判别x和y是否属于同一集合。

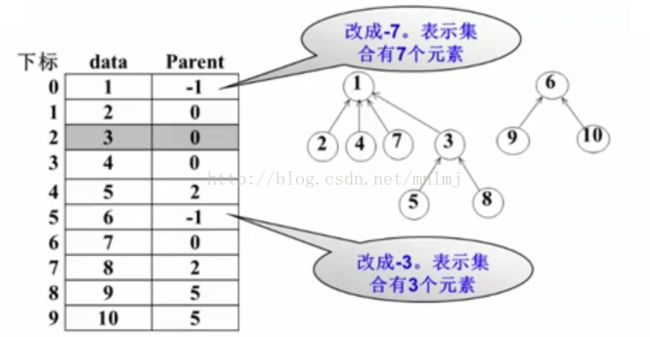
〖例〗有三个整数集合 S1={1,2,4,7}，S2={3,5,8}，S3={6,9,10}

* 双亲表示法：孩子指向双亲。

* 采用数组存储形式——parent位置为负数(-1)表示根结点；非负数表示指向父亲结点的下标位置。

2、集合运算
（1）查找某个元素所在的集合（用根结点表示）

（2） 集合的并运算
① 分别找到X1和X2两个元素所在集合树的根结点
② 如果它们不同根，则将其中一个根结点的父结点指针设置成另一个根结点的数组下标。

* 树越来越高导致Find效率变低：为了改善合并以后的查找性能，可以采用小的集合合并到相对大的集合中。（修改Union函数）

* 需要记录集合中元素个数：parent 负数的绝对值可以用来表示根节点下有几个元素