TreeMap工作原理
一、红黑树简介
TreeMap是通过红黑树实现的,增删改查的操作底层都是对红黑树的相关操作,因此先介绍红黑树的相关性质。
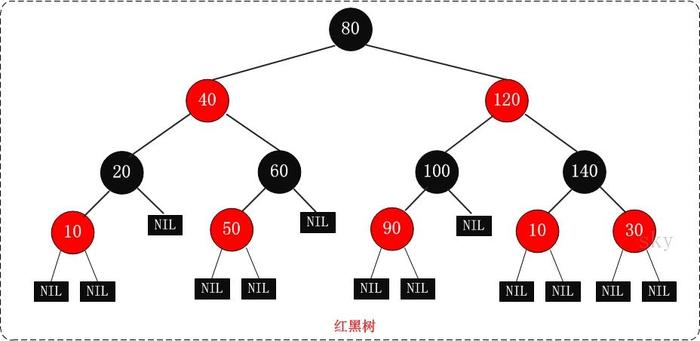
红黑树顾名思义就是节点是红色或者黑色的平衡二叉树,它通过颜色的约束来维持着二叉树的平衡。对于一棵有效的红黑树二叉树而言我们必须增加如下规则:
1、每个节点都只能是红色或者黑色
2、根节点是黑色
3、每个叶节点(null节点,空节点)是黑色的。
4、如果一个结点是红的,则它两个子节点都是黑的。也就是说在一条路径上不能出现相邻的两个红色结点。
5、从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。
上面的约束强制了红黑树的关键性质:从根到叶子的最长的可能路径不多于最短的可能路径的两倍长。因此这棵树大致上是平衡的。
二、TreeMap数据结构
TreeMap的定义如下:
public class TreeMap<K,V>
extends AbstractMap<K,V>
implements NavigableMap<K,V>, Cloneable, java.io.Serializable
TreeMap中的属性:
private final Comparatorsuper K> comparator;
private transient Entry root;
/**
* The number of entries in the tree
*/
private transient int size = 0;
/**
* The number of structural modifications to the tree.
*/
private transient int modCount = 0;
/**
* Fields initialized to contain an instance of the entry set view
* the first time this view is requested. Views are stateless, so
* there's no reason to create more than one.
*/
private transient EntrySet entrySet;
private transient KeySet navigableKeySet;
private transient NavigableMap descendingMap;
// Red-black mechanics
private static final boolean RED = false;
private static final boolean BLACK = true;
**三、TreeMap put()方法 **
在了解TreeMap的put()方法之前,我们先了解红黑树增加节点的算法。
红黑树增加节点
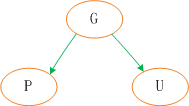
红黑树在新增节点过程中比较复杂,复杂归复杂它同样必须要依据上面提到的五点规范,同时由于规则1、2、3基本都会满足,下面我们主要讨论规则4、5。假设我们这里有一棵最简单的树,我们规定新增的节点为N、它的父节点为P、P的兄弟节点为U、P的父节点为G。
对于新节点的插入有如下三个关键地方:
1、插入新节点总是红色节点 。
2、如果插入节点的父节点是黑色, 能维持性质 。
3、如果插入节点的父节点是红色, 破坏了性质. 故插入算法就是通过重新着色或旋转, 来维持性质 。
一、根节点
若新插入的节点N没有父节点,则直接当做根据节点插入即可,同时将颜色设置为黑色,如图(1)。
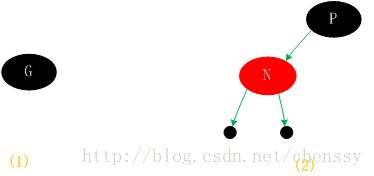
二、父节点为黑色
这种情况新节点N同样是直接插入,同时颜色为红色,由于根据规则四它会存在两个黑色的叶子节点,值为null。同时由于新增节点N为红色,所以通过它的子节点的路径依然会保存着相同的黑色节点数,同样满足规则5,如图(2)。
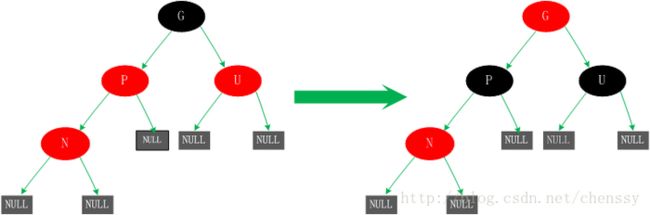
三、若父节点P和P的兄弟节点U都为红色
对于这种情况若直接插入肯定会出现不平衡现象。怎么处理?P、U节点变黑、G节点变红。这时由于经过节点P、U的路径都必须经过G所以在这些路径上面的黑节点数目还是相同的。但是经过上面的处理,可能G节点的父节点也是红色,这个时候我们需要将G节点当做新增节点递归处理。
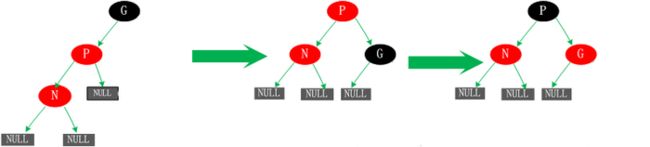
四、若父节点P为红色,叔父节点U为黑色或者缺少,且新增节点N为P节点的右孩子
对于这种情况我们对新增节点N、P进行一次左旋转。这里所产生的结果其实并没有完成,还不是平衡的(违反了规则四),这时候我们需要进行情况5的操作。
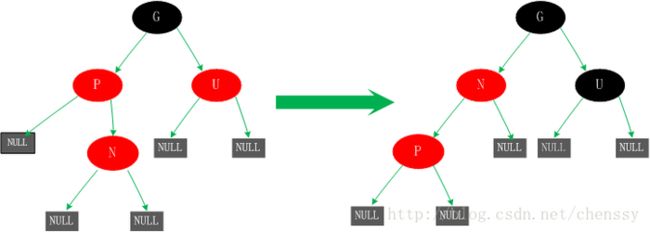
五、父节点P为红色,叔父节点U为黑色或者缺少,新增节点N为父节点P左孩子这种情况有可能是由于情况四而产生的,也有可能不是。
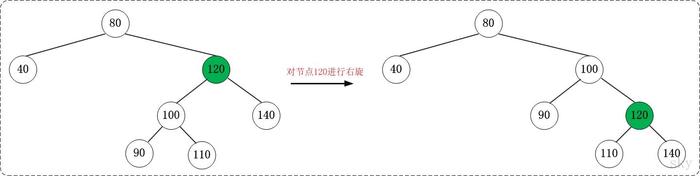
对于这种情况先以P节点为中心进行右旋转,在旋转后产生的树中,节点P是节点N、G的父节点。但是这棵树并不规范,它违反了规则4,所以我们将P、G节点的颜色进行交换,使之其满足规范。开始时所有的路径都需要经过G其他们的黑色节点数一样,但是现在所有的路径改为经过P,且P为整棵树的唯一黑色节点,所以调整后的树同样满足规范5。
上面展示了红黑树新增节点的五种情况,这五种情况涵盖了所有的新增可能,不管这棵红黑树多么复杂,都可以根据这五种情况来进行生成。下面就来分析Java中的TreeMap是如何来实现红黑树的。
TreeMap put()方法实现分析
在TreeMap的put()的实现方法中主要分为两个步骤:
1)构建排序二叉树;
2)平衡二叉树。
对于排序二叉树的创建,其添加节点的过程如下:
1、以根节点为初始节点进行检索。
2、与当前节点进行比对,若新增节点值较大,则以当前节点的右子节点作为新的当前节点。否则以当前节点的左子节点作为新的当前节点。
3、循环递归2步骤知道检索出合适的叶子节点为止。
4、将新增节点与3步骤中找到的节点进行比对,如果新增节点较大,则添加为右子节点;否则添加为左子节点。
下面分析TreeMap的put源码:
public V put(K key, V value) {
Entry t = root;
if (t == null) {
//此时TreeMap为空树,将该节点作为根节点;
compare(key, key); // type (and possibly null) check
root = new Entry<>(key, value, null);
size = 1;
modCount++;
return null;
}
int cmp;
Entry parent;
// split comparator and comparable paths
Comparator super K> cpr = comparator;
//判断是否存在比较器;
if (cpr != null) {
do {
//递归遍历,找出要插入节点的位置;如果该节点的key值已存在,则直接替换;
parent = t;
cmp = cpr.compare(key, t.key);
if (cmp < 0)
t = t.left;
else if (cmp > 0)
t = t.right;
else
return t.setValue(value);
} while (t != null);
}
else {
if (key == null)
throw new NullPointerException();
@SuppressWarnings("unchecked")
Comparable super K> k = (Comparable super K>) key;
do {
parent = t;
cmp = k.compareTo(t.key);
if (cmp < 0)
t = t.left;
else if (cmp > 0)
t = t.right;
else
return t.setValue(value);
} while (t != null);
}
Entry e = new Entry<>(key, value, parent);
//根据比较器的结果将新节点插入到TreeMap中;
if (cmp < 0)
parent.left = e;
else
parent.right = e;
//fixAfterInsertion()方法就是对这棵树进行调整、平衡
//而所有的可能性总共有5种情况;
fixAfterInsertion(e);
size++;
modCount++;
return null;
}
/** From CLR */
private void fixAfterInsertion(Entry x) {
x.color = RED; //新插入的节点颜色初始化为红色;
while (x != null && x != root && x.parent.color == RED) {
//父节点为红色
//父节点为左孩子
if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {
//获取叔父节点
Entry y = rightOf(parentOf(parentOf(x)));
if (colorOf(y) == RED) {
//叔父节点为红色,情况三
//父节点着色为黑色
setColor(parentOf(x), BLACK);
//叔父节点着色为黑色
setColor(y, BLACK);
//父节点的父节点着色为红色
setColor(parentOf(parentOf(x)), RED);
//将父节点的父节点当做新增节点,递归处理;
x = parentOf(parentOf(x));
} else {
//叔父节点为黑色,有两种可能:情况四和情况五;最终都转化为情况五;
//如果新增节点为右孩子,情况四
if (x == rightOf(parentOf(x))) {
x = parentOf(x);
//对父节点进行左旋,让新增节点变成左孩子;
rotateLeft(x);
}
//情况五,此时父节点和子节点都在左侧(1),可以和(2)进行比较
//将父节点着色为黑色
setColor(parentOf(x), BLACK);
//将父节点的父节点着色为红色
setColor(parentOf(parentOf(x)), RED);
//对父节点的父节点进行右旋
rotateRight(parentOf(parentOf(x)));
}
} else {
//父节点为右孩子
//获取叔父节点
Entry y = leftOf(parentOf(parentOf(x)));
if (colorOf(y) == RED) {
//叔父节点为红色,情况三
//将父节点着色为黑色
setColor(parentOf(x), BLACK);
//将叔父节点着色为黑色
setColor(y, BLACK);
//将父节点的父节点着色为红色
setColor(parentOf(parentOf(x)), RED);
//递归处理父节点的父节点当做新增节点递归处理
x = parentOf(parentOf(x));
} else {
//如果X的叔节点(U为黑色);这里会存在两种情况(情况四、情况五)
if (x == leftOf(parentOf(x))) {
//如果新增节点是左孩子,情况四
x = parentOf(x);
//将父节点右旋
rotateRight(x);
}
//情况五,此时父节点和子节点都在右侧(2),可以和(1)进行比较
//将父节点着色为黑色
setColor(parentOf(x), BLACK);
//将父节点的父节点着色为红色
setColor(parentOf(parentOf(x)), RED);
//对父节点的父节点进行左旋
rotateLeft(parentOf(parentOf(x)));
}
}
}
//情况一,新插入的节点N没有父节点,直接插入节点,将颜色设置为黑色;
root.color = BLACK;
}
TreeMap的put源码分析结束;
其实到这里,TreeMap的delete/deleteEntry等操作都基本是相同的思想进行实现的,就不再详细展开了,有兴趣的可以再分析下去。
作者:DepaX
链接:https://www.jianshu.com/p/433a1e265b65
來源:简书
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
=========================================================
4.1 TreeMap
在Map集合框架中,除了HashMap以外,TreeMap也是我们工作中常用到的集合对象之一。
与HashMap相比,TreeMap是一个能比较元素大小的Map集合,会对传入的key进行了大小排序。其中,可以使用元素的自然顺序,也可以使用集合中自定义的比较器来进行排序;
不同于HashMap的哈希映射,TreeMap底层实现了树形结构,至于具体形态,你可以简单的理解为一颗倒过来的树---根在上--叶在下。如果用计算机术语来说的话,TreeMap实现了红黑树的结构,形成了一颗二叉树。
至于什么是二叉树,什么是红黑树,我们后面再谈,你现在只需要记住它是一颗倒过来的树,就OK了。
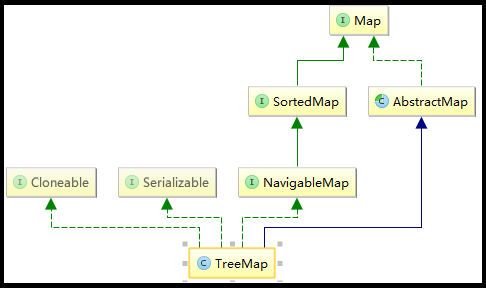
TreeMap继承于AbstractMap,实现了Map, Cloneable, NavigableMap, Serializable接口。
(1)TreeMap 继承于AbstractMap,而AbstractMap实现了Map接口,并实现了Map接口中定义的方法,减少了其子类继承的复杂度;
(2)TreeMap 实现了Map接口,成为Map框架中的一员,可以包含着key--value形式的元素;
(3)TreeMap 实现了NavigableMap接口,意味着拥有了更强的元素搜索能力;
(4)TreeMap 实现了Cloneable接口,实现了clone()方法,可以被克隆;
(5)TreeMap 实现了Java.io.Serializable接口,支持序列化操作,可通过Hessian协议进行传输;
对于Cloneable, Serializable来说,我们再熟悉不过,基本上Java集合框架中的每一个类都会实现这2个接口,而NavigableMap接口是干什么的,它定义了什么样的功能?接下来,我们就通过NavigableMap的源码来看下!
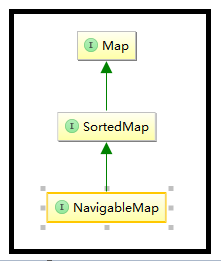
根据上面的截图,我们首先介绍下NavigableMap体系中的SortedMap接口:
对于SortedMap来说,该类是TreeMap体系中的父接口,也是区别于HashMap体系最关键的一个接口。
主要原因就是SortedMap接口中定义的第一个方法---Comparator comparator();
该方法决定了TreeMap体系的走向,有了比较器,就可以对插入的元素进行排序了;
public interface SortedMap<K,V> extends Map<K,V> {
//返回元素比较器。如果是自然顺序,则返回null;
Comparatorsuper K> comparator();
//返回从fromKey到toKey的集合:含头不含尾
java.util.SortedMap subMap(K fromKey, K toKey) ;
//返回从头到toKey的集合:不包含toKey
java.util.SortedMap headMap(K toKey) ;
//返回从fromKey到结尾的集合:包含fromKey
java.util.SortedMap tailMap(K fromKey) ;
//返回集合中的第一个元素:
K firstKey();
//返回集合中的最后一个元素:
K lastKey();
//返回集合中所有key的集合:
Set keySet() ;
//返回集合中所有value的集合:
Collection values() ;
//返回集合中的元素映射:
Set> entrySet();
}
上面介绍了SortedMap接口,而NavigableMap接口又是对SortedMap进一步的扩展:主要增加了对集合内元素的搜索获取操作,例如:返回集合中某一区间内的元素、返回小于大于某一值的元素等类似操作。
public interface NavigableMap<K,V> extends SortedMap<K,V> {
//返回小于key的第一个元素:
Map.Entry lowerEntry(K key) ;
//返回小于key的第一个键:
K lowerKey(K key);
//返回小于等于key的第一个元素:
Map.Entry floorEntry(K key) ;
//返回小于等于key的第一个键:
K floorKey(K key);
//返回大于或者等于key的第一个元素:
Map.Entry ceilingEntry(K key) ;
//返回大于或者等于key的第一个键:
K ceilingKey(K key);
//返回大于key的第一个元素:
Map.Entry higherEntry(K key) ;
//返回大于key的第一个键:
K higherKey(K key);
//返回集合中第一个元素:
Map.Entry firstEntry() ;
//返回集合中最后一个元素:
Map.Entry lastEntry() ;
//返回集合中第一个元素,并从集合中删除:
Map.Entry pollFirstEntry() ;
//返回集合中最后一个元素,并从集合中删除:
Map.Entry pollLastEntry() ;
//返回倒序的Map集合:
java.util.NavigableMap descendingMap() ;
NavigableSet navigableKeySet() ;
//返回Map集合中倒序的Key组成的Set集合:
NavigableSet descendingKeySet() ;
java.util.NavigableMap subMap(K fromKey, boolean fromInclusive,
K toKey, boolean toInclusive) ;
java.util.NavigableMap headMap(K toKey, boolean inclusive) ;
java.util.NavigableMap tailMap(K fromKey, boolean inclusive) ;
SortedMap subMap(K fromKey, K toKey) ;
SortedMap headMap(K toKey) ;
SortedMap tailMap(K fromKey) ;
}
其实,NavigableMap的目的很简单、很直接,就是增强了对集合内元素的搜索、获取的功能,当子类TreeMap实现时,自然获取以上的功能;
TreeMap具有如下特点:
不允许出现重复的key;
可以插入null键,null值;
可以对元素进行排序;
无序集合(插入和遍历顺序不一致);
4.2 TreeMap基本操作
public class TreeMapTest {
public static void main(String[] agrs){
//创建TreeMap对象:
TreeMap<String,Integer> treeMap = new TreeMap<String,Integer>();
System.out.println("初始化后,TreeMap元素个数为:" + treeMap.size());
//新增元素:
treeMap.put("hello",1);
treeMap.put("world",2);
treeMap.put("my",3);
treeMap.put("name",4);
treeMap.put("is",5);
treeMap.put("jiaboyan",6);
treeMap.put("i",6);
treeMap.put("am",6);
treeMap.put("a",6);
treeMap.put("developer",6);
System.out.println("添加元素后,TreeMap元素个数为:" + treeMap.size());
//遍历元素:
Set<Map.Entry<String,Integer>> entrySet = treeMap.entrySet();
for(Map.Entry<String,Integer> entry : entrySet){
String key = entry.getKey();
Integer value = entry.getValue();
System.out.println("TreeMap元素的key:"+key+",value:"+value);
}
//获取所有的key:
Set<String> keySet = treeMap.keySet();
for(String strKey:keySet){
System.out.println("TreeMap集合中的key:"+strKey);
}
//获取所有的value:
Collection valueList = treeMap.values();
for(Integer intValue:valueList){
System.out.println("TreeMap集合中的value:" + intValue);
}
//获取元素:
Integer getValue = treeMap.get("jiaboyan");//获取集合内元素key为"jiaboyan"的值
String firstKey = treeMap.firstKey();//获取集合内第一个元素
String lastKey =treeMap.lastKey();//获取集合内最后一个元素
String lowerKey =treeMap.lowerKey("jiaboyan");//获取集合内的key小于"jiaboyan"的key
String ceilingKey =treeMap.ceilingKey("jiaboyan");//获取集合内的key大于等于"jiaboyan"的key
SortedMap<String,Integer> sortedMap =treeMap.subMap("a","my");//获取集合的key从"a"到"jiaboyan"的元素
//删除元素:
Integer removeValue = treeMap.remove("jiaboyan");//删除集合中key为"jiaboyan"的元素
treeMap.clear(); //清空集合元素:
//判断方法:
boolean isEmpty = treeMap.isEmpty();//判断集合是否为空
boolean isContain = treeMap.containsKey("jiaboyan");//判断集合的key中是否包含"jiaboyan"
}
}
4.3 TreeMap排序
上一节,通过代码展示出TreeMap简单使用。而早在第一小节,笔者就说过TreeMap是一个可以对元素进行排序的集合,那么究竟怎么排序呢?
(1)使用元素自然排序
在使用自然顺序排序时候,需要区分两种情况:一种是Jdk定义的对象,一种是我们应用自己定义的对象;
public class SortedTest implements Comparable<SortedTest> {
private int age;
public SortedTest(int age){
this.age = age;
}
public int getAge() {
return age;
}
public void setAge(int age) {
this.age = age;
}
//自定义对象,实现compareTo(T o)方法:
public int compareTo(SortedTest sortedTest) {
int num = this.age - sortedTest.getAge();
//为0时候,两者相同:
if(num==0){
return 0;
//大于0时,传入的参数小:
}else if(num>0){
return 1;
//小于0时,传入的参数大:
}else{
return -1;
}
}
}
public class TreeMapTest {
public static void main(String[] agrs){
//自然顺序比较
naturalSort();
}
//自然排序顺序:
public static void naturalSort(){
//第一种情况:Integer对象
TreeMap treeMapFirst = new TreeMap();
treeMapFirst.put(1,"jiaboyan");
treeMapFirst.put(6,"jiaboyan");
treeMapFirst.put(3,"jiaboyan");
treeMapFirst.put(10,"jiaboyan");
treeMapFirst.put(7,"jiaboyan");
treeMapFirst.put(13,"jiaboyan");
System.out.println(treeMapFirst.toString());
//第二种情况:SortedTest对象
TreeMap treeMapSecond = new TreeMap();
treeMapSecond.put(new SortedTest(10),"jiaboyan");
treeMapSecond.put(new SortedTest(1),"jiaboyan");
treeMapSecond.put(new SortedTest(13),"jiaboyan");
treeMapSecond.put(new SortedTest(4),"jiaboyan");
treeMapSecond.put(new SortedTest(0),"jiaboyan");
treeMapSecond.put(new SortedTest(9),"jiaboyan");
System.out.println(treeMapSecond.toString());
}
}
在自然顺序比较中,需要让被比较的元素实现Comparable接口,否则在向集合里添加元素时报:"java.lang.ClassCastException: com.jiaboyan.collection.map.SortedTest cannot be cast to java.lang.Comparable"异常;
这是因为在调用put()方法时,会将传入的元素转化成Comparable类型对象,所以当你传入的元素没有实现Comparable接口时,就无法转换,遍会报错;
(2)使用自定义比较器排序
使用自定义比较器排序,需要在创建TreeMap对象时,将自定义比较器对象传入到TreeMap构造方法中;
自定义比较器对象,需要实现Comparator接口,并实现比较方法compare(T o1,T o2);
值得一提的是,使用自定义比较器排序的话,被比较的对象无需再实现Comparable接口了;
public class SortedTest {
private int age;
public SortedTest(int age){
this.age = age;
}
public int getAge() {
return age;
}
public void setAge(int age) {
this.age = age;
}
}
public class SortedTestComparator implements Comparator<SortedTest> {
//自定义比较器:实现compare(T o1,T o2)方法:
public int compare(SortedTest sortedTest1, SortedTest sortedTest2) {
int num = sortedTest1.getAge() - sortedTest2.getAge();
if(num==0){//为0时候,两者相同:
return 0;
}else if(num>0){//大于0时,后面的参数小:
return 1;
}else{//小于0时,前面的参数小:
return -1;
}
}
}
public class TreeMapTest {
public static void main(String[] agrs){
//自定义顺序比较
customSort();
}
//自定义排序顺序:
public static void customSort(){
TreeMap treeMap = new TreeMap(new SortedTestComparator());
treeMap.put(new SortedTest(10),"hello");
treeMap.put(new SortedTest(21),"my");
treeMap.put(new SortedTest(15),"name");
treeMap.put(new SortedTest(2),"is");
treeMap.put(new SortedTest(1),"jiaboyan");
treeMap.put(new SortedTest(7),"world");
System.out.println(treeMap.toString());
}
}
4.4 树的自我介绍
在具体讲解TreeMap底层结构之前,我们有必要先来了解下树!
那么,到底什么是树呢?
树--是计算机中的一种数据结构,是一个由n(>=1)个元素组成具有层次关系的集合。因该数据结构呈现出的形状像一颗树,所以称这种数据结构叫做树,只不过这颗树是倒过来的。
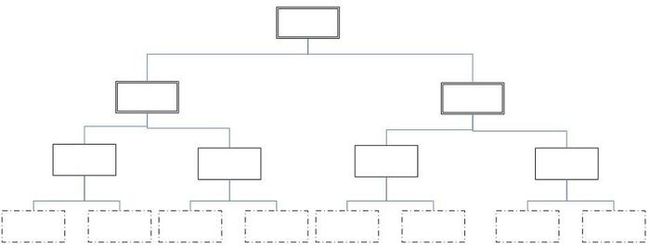
在上面的截图中,简单抽象出数据结构中的树。在生活中,这样的结构比比皆是,例如:公司的组织架构、家族的族谱、计算机中的文件结构等等。只要符合上面的结构,均可以称为树;
在计算机领域中,树只是一种简称,具体的实现还是交由其子树来完成;这其中就包括:二叉树、平衡二叉树、红黑树、B树、哈夫曼树等。在本章节中,我们主要介绍其中的两种数据结构---二叉树、红黑树;
在介绍二叉树之前,还需要对树的相关术语进行理解:
举个图片来说,更加直观:(只为讲解树的概念)
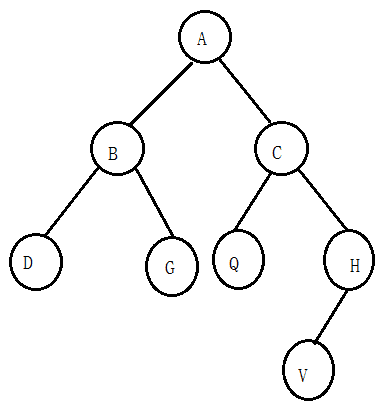
节点(Nood):树中的每一个元素都叫做节点,又或者称为结点;图中A、B、C、D等都称之为节点;
根节点(树根-Root):在树中,最顶端的节点称之为根节点(树根-Root);A节点就是整个树的根节点;
子树:除了根节点之外,其余节点自由组合成的树,称之为子树,子树可以是一个节点,也可以是多个节点;其中,Q节点可称之为子树,B、D、G三个节点结合也可以称之为子树;
叶子节点(叶节点):没有孩子节点的节点,称之为叶子节点(叶节点),也就是该节点下面没有子节点了;图中D、G、Q、V称之为叶子节点;
父节点:简单来说,就是一个节点上面的节点,就是该节点的父节点;B节点是D节点的父节点,C节点是Q节点的父节点;
树的高度:从叶子节点(此时高度为1)开始自底向上逐层增加,得到的值称之为树的高度;截图中树的高度为4(V、H、C、A);
树的深度:从根节点(此时深度为1)开始自上而下逐层增加,最终得到的值称之为树的深度;截图中树的深度为4(A、C、H、V);
4.5 二叉树
二叉树是最基础的树结构,也是树结构中的根基;
二叉树可以有多个元素,也可以只有一个元素,当然也可以一个元素也没有,它是一个元素的集合;二叉树规定了在每个节点下最多只能拥有两个子节点,一左一右;其中,左节点可以称为左子树,右节点称为右子树;但没有要求左子树中任意节点的值要小于右子树中任意节点的值。
说到这,暂时我们可以简单地将二叉树理解成链表,只不过这个链表被从中间进行了分隔,一边朝右,一边朝左,就形成了一颗二叉树。
二叉树节点实现:
public class TreeNode {
//节点的值:
private int data;
//指向左孩子的指针:
private TreeNode leftTreeNode;
//指向右孩子的指针:
private TreeNode rightTreeNode;
//指向父节点的指针
private TreeNode parentNode;
public TreeNode(int data, TreeNode leftTreeNode,
TreeNode rightTreeNode, TreeNode parentNode) {
this.data = data;
this.leftTreeNode = leftTreeNode;
this.rightTreeNode = rightTreeNode;
this.parentNode = parentNode;
}
public int getData() {
return data;
}
public void setData(int data) {
this.data = data;
}
public TreeNode getLeftTreeNode() {
return leftTreeNode;
}
public void setLeftTreeNode(TreeNode leftTreeNode) {
this.leftTreeNode = leftTreeNode;
}
public TreeNode getRightTreeNode() {
return rightTreeNode;
}
public void setRightTreeNode(TreeNode rightTreeNode) {
this.rightTreeNode = rightTreeNode;
}
public TreeNode getParentNode() {return parentNode;}
public void setParentNode(TreeNode parentNode) {this.parentNode = parentNode;}
}
4.6 二叉查找树
说完了二叉树,下面继续说二叉查找树;相比于二叉树来说,二叉查找树的特点更加明确。
二叉查找树规定:
如果二叉查找树的左子树不为空,那么它的左子树上的任意节点的值都小于根节点的值;
如果二叉查找树的右子树不为空,那么它的右子树上的任意节点的值都大于根节点的值;
也就是说,二叉查找树的左子树中任意节点的值都小于右子树中任意节点的值。而且,在左子树和右子树中也同样形成了二叉查找树;所以说二叉查找树的特点比二叉树更加明确。
此外,根据上面的特点,我们还可以使用二分查找在树中进行元素搜索:如果查找的元素大于根节点,则在树的右边进行搜索;如果小于根节点,则在树的左边进行搜索。如果等于根节点,则直接返回;所以二叉查找树的查询效率远远高于二叉树。
4.8 平衡二叉树(AVL树)
前几节中,笔者说过:可以将二叉树简单地理解为一个链表结构。当时,是为了能让各位能对二叉树有一个最直观的理解。
其实,在具体的实现中二叉树确实会形成一个链表结构。
试想下,如果一个二叉树的左子树为空,只有右子树,且右子树中又只有右节点(左节点),那么这个二叉树就形成了一个不折不扣的链表。对于二叉查找树来说,二分查找也就失去了原有的性能,变成了顺序查找。即元素的插入顺序是1、2、3、4、5、6的话,即可实现。
为了针对这一情况,平衡二叉树出现了(又称为AVL树),它要求左右子树的高度差的绝对值不能大于1,也就是说左右子树的高度差只能为-1、0、1。
4.7 红黑树
终于说到了今天的重中之重--红黑树,相比于之前讲过的数据结构,红黑树的难度有所增加,你要做好准备!
只要带有树字,它就远离不了二叉树的结构。
红黑树,本质上依旧一颗二叉查找树,它满足了二叉查找树的特点,即左子树任意节点的值永远小于右子树任意节点的值。
不过,二叉查找树还有一个致命的弱点,即左子树(右子树)可以为空,而插入的节点全部集中到了树的另一端,致使二叉查找树失去了平衡,二叉查找树搜索性能下降,从而失去了使用二分查找的意义。
为了维护树的平衡性,平衡二叉树(AVL树)出现了,它用左右子树的高度差来保持着树的平衡。而我们本节要介绍的红黑树,用的是节点的颜色来维持树的平衡。
那么,红黑树是怎么利用颜色来维持平衡的呢?接下来,让我们慢慢道来。
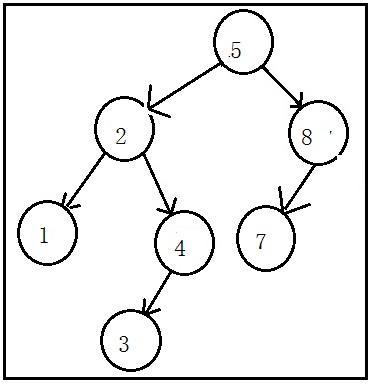
红黑树,即红颜色和黑颜色并存的二叉树,插入的元素节点会被赋为红色或者黑色,待所有元素插入完成后就形成了一颗完整的红黑树。如下图所示:
不过,你不要想当然的以为只是给二叉树的阶段随意赋为黑色或者红色,就可保证树的平衡。事情远没有你想象的那么简单。
一颗红黑树必须满足一下几点要求:
树中每个节点必须是有颜色的,要么红色,要么黑色;
树中的根节点必须是黑色的;
树中的叶节点必须是黑色的,也就是树尾的NIL节点或者为null的节点;
树中任意一个节点如果是红色的,那么它的两个子节点一点是黑色的;
任意节点到叶节点(树最下面一个节点)的每一条路径所包含的黑色节点数目一定相同;
科普:NIL节点是就是一个假想的或是无实在意义的节点,所有应该指向NULL的指针,都看成指向了NIL节点。包括叶节点的子节点指针或是根节点的父指针(均是指向null的)
除了给节点赋颜色之外,还会对节点进行左旋、右旋操作,以来维持树的平衡。那么,左旋、右旋又什么?
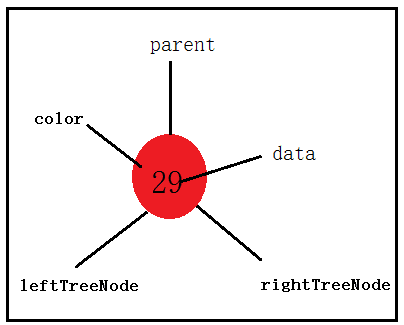
首先,我们先来看下在红黑树中,每一个节点的数据结构是什么样子的?
public class TreeNode {
//节点的值:
private int data;
//节点的颜色:
private String color;
//指向左孩子的指针:
private TreeNode leftTreeNode;
//指向右孩子的指针:
private TreeNode rightTreeNode;
//指向父节点的指针
private TreeNode parentNode;
public TreeNode(int data, String color, TreeNode leftTreeNode,
TreeNode rightTreeNode, TreeNode parentNode) {
this.data = data;
this.color = color;
this.leftTreeNode = leftTreeNode;
this.rightTreeNode = rightTreeNode;
this.parentNode = parentNode;
}
public int getData() {
return data;
}
public void setData(int data) {
this.data = data;
}
public String getColor() {return color;}
public void setColor(String color) {this.color = color;}
public TreeNode getLeftTreeNode() {
return leftTreeNode;
}
public void setLeftTreeNode(TreeNode leftTreeNode) {
this.leftTreeNode = leftTreeNode;
}
public TreeNode getRightTreeNode() {
return rightTreeNode;
}
public void setRightTreeNode(TreeNode rightTreeNode) {
this.rightTreeNode = rightTreeNode;
}
public TreeNode getParentNode() {return parentNode;}
public void setParentNode(TreeNode parentNode) {this.parentNode = parentNode;}
}
如果用图片来形容的话:
4.7.1 旋转
上面说过,为了维护红黑树的平衡,不只是给节点着色那么简单,还有更复杂的处理逻辑。
而这更复杂的处理逻辑就是对节点进行旋转操作,其中旋转操作又分为左旋、右旋两种;
对于树的操作,最常见的就是添加、删除而已。不过,在添加或者删除之后,红黑树发生了改变,可能就不满足以上的5点要求,也就不是一颗红黑树了。于是我们需要通过对节点的旋转,使其重新成为一颗红黑树。
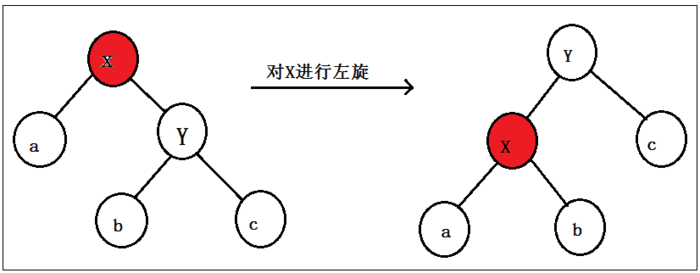
- 左旋
左旋,顾名思义就是对节点进行向左旋转处理;
对节点X进行向左进行旋转,将其变成了一个左子节点;
这个左旋中的左,就是将被旋转的节点变成一个左节点;
其中,如果Y的的左子节点不为null,则将其赋值X的右子节点;
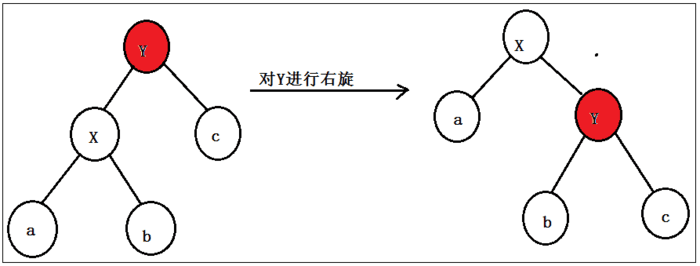
- 右旋
右旋,同理,也就是对节点进行向右旋转处理;
对节点Y进行向右进行旋转,将其变成了一个右子节点;
这个右旋中的右,就是将被旋转的节点变成一个右节点;
其中,如果X节点的右子节点不为null,则赋值给Y的左子节点;
补充:在举个例子,让大家更直观的理解:(暂时先忽略红黑树,只关注旋转)
4.7.2 红黑树节点添加
本节中,笔者就来介绍下红黑树节点的添加。
在将一个节点插入到红黑树中,首选需要将红黑树当做一颗二叉树查找树来对待,将节点进行插入。然后,为新插入的节点进行着色;最后,通过旋转和重新着色的方式来修正树的平衡,使其成为一颗红黑树;
(1)对于红黑树来说,其底层依旧是一颗二叉查找树。当我们插入新的元素时,它依旧会对该元素进行排序比较,将其送入到左子树或者是右子树中。
(2)在将新节点安置好以后,在对其进行着色处理,必须着成红色。
你此时可能会问,为什么要着成红色,而不是黑色呢?
这就需要我们重新回顾下红黑树的规范了:
1. 树中每个节点必须是有颜色的,要么红色,要么黑色;
2. 树中的根节点必须是黑色的;
3. 树中的叶节点必须是黑色的,也就是树尾的NIL节点或者为null的节点;
4. 树中任意一个节点如果是红色的,那么它的两个子节点一点是黑色的;
5. 任意节点到叶节点(树最下面一个节点)的每一条路径所包含的黑色节点数目一定相同;
通过以上的规范,我们可以分析出,当将新增节点着成红色后,我们违背以上规范的条数最少,恢复平衡起来最省事,当新增节点为红色时:
1.不会违背第五条--黑色节点数目相同;
2.不会违背第一条--节点必须是红色,或者黑色;
3.不会违背第二条--根节点是黑色--当树中已有元素时候,我们新增节点并不会影响根节点的颜色(若树中没有元素,新增节点会被当成根节点,此时虽被着为红色,但在最后一步中还会对其重新着色,变成黑色);
4.不会违背第三条--此处所指的叶节点指的是叶节点的子节点,也就是为null的元素;
5.可能会违背第四条--任意节点为红色,其子节点一定是黑色;
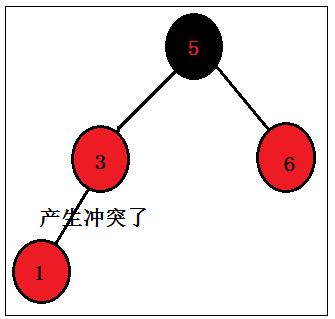
如果新插入的节点的父节点是红色的话,那么第四条一定会违背,所以说我们需要对其进行旋转处理;
(3)冲突来了,解决冲突(对节点进行旋转)
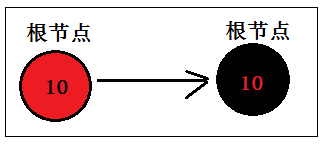
当被插入节点是根节点:
新插入的节点后,如果为根节点,则直接将其变成黑色,并返回;
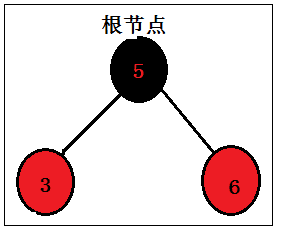
当被插入节点的父节点是黑色:
新插入的节点被着成红色后,发现其父节点是黑色,并不影响红黑树结构,所以并不需要对平衡性做处理,直接返回;
当被插入节点的父节点是红色(最复杂):
新插入的节点被着成红色后,发现其父节点是红色,此时红黑树的平衡被打破,需要特别处理。
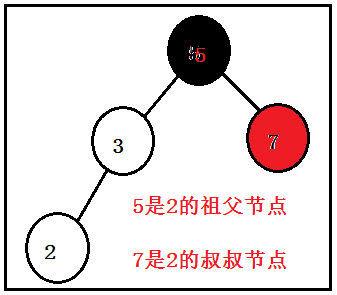
说之前,简单的阐述下什么是该节点的祖父节点,什么是该节点的叔叔节点(画图一目了然);
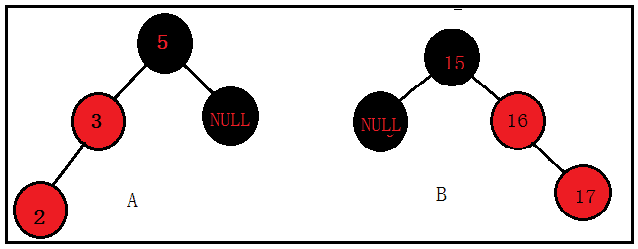
case1:叔叔节点为黑色(空节点默认为黑色)
A.2是3的左子节点,3是5的左子节点;
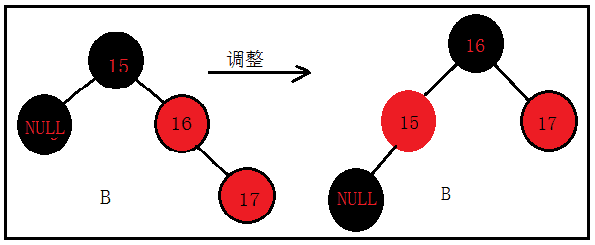
B.17是16的右子节点,16是15的右子节点;
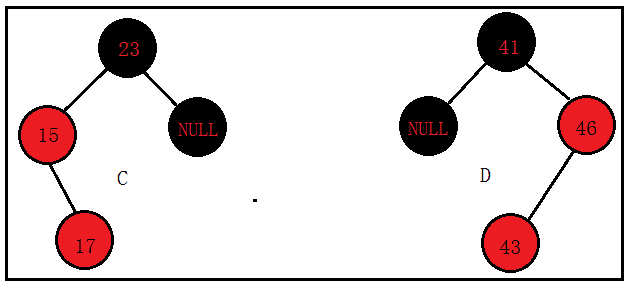
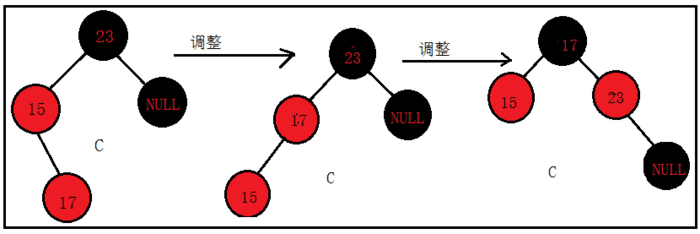
C.17是15的右子节点,15是23的左子节点
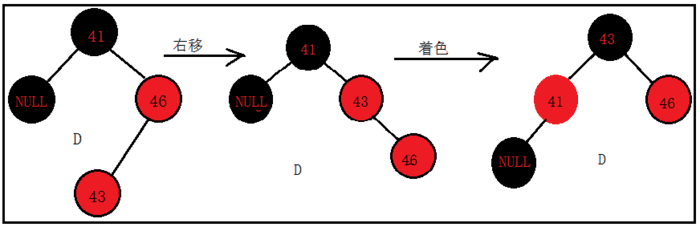
D.43是56的左子节点,46是41的右子节点;
其中,A、B称之为外侧插入,C、D称之为内测插入。
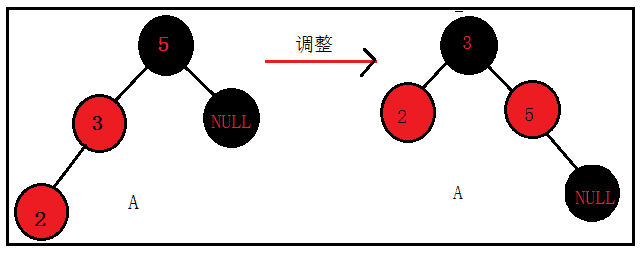
首先,来看A的解决方案:
将3设置为黑色,5设置为红色,再对5进行右旋,结果如下:
来看B的解决方案:
将16设置为黑色,15设置为红色,再对15进行左旋,结果如下:
来看C的解决方案:
将15进行左旋,成为17的左子节点,此时形成了A情况,再将17置为黑色,23置为红色,再对23进行右旋,结果如下:
来看D的解决方案:
将46进行右旋,成为41的右子节点,此时形成了B情况,再将43置为黑色,41置为红色,再对41进行左旋,结果如下:
case2:叔叔节点为红色
当叔叔节点为红色时,处理的逻辑较为简单,主要对元素节点的颜色进行处理,无需左旋、右旋的操作。
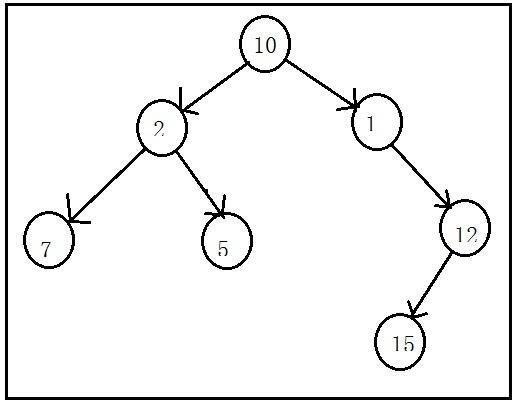
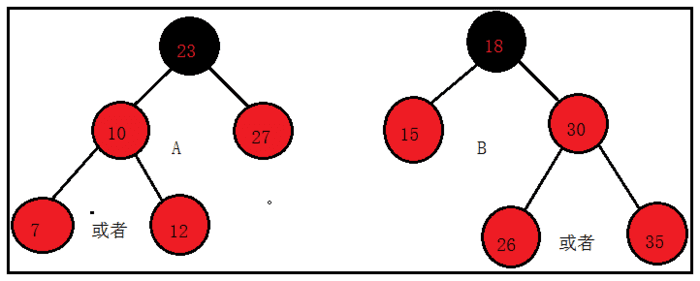
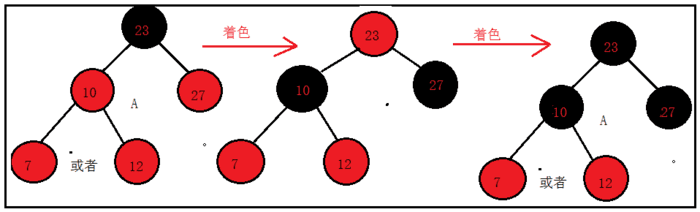
在A情况中,无论新插入的元素是7还是12,处理过程都是一样的;
将10和27置为黑色,23置为红色,再将23置为黑色,新插入元素7(12)保持红色不变,结束返回;
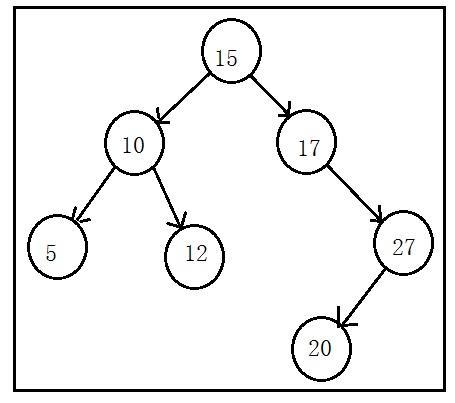
同理,在B情况中,处理26或者35的逻辑也是相同的;
将15和30置为黑色,18置为红色,再将18置为黑色,新插入元素26(35)保持红色不变,结束返回;
同上,暂不画图了;
以上,就是红黑树添加节点的处理逻辑,希望以上的图片可以让你对着色、旋转有一个清晰的认识!
有兴趣的朋友,可以参考红黑树网站进行实际操作!
4.7.3 红黑树节点删除
暂省略;
4.8 TreeMap源码讲解(基于JDK1.7.0_75)
上面,我们通过图片的形式,对红黑树进行了全面的讲解。接下来,就让我们学习下红黑树在Java中的实现--TreeMap;
- TreeMap节点结构
TreeMap底层存储结构与HashMap基本相同,依旧是Entry对象,存储key--value键值对,子节点的引用和父节点的引用,以及默认的节点颜色(黑色);
static final class Entry<K,V> implements Map.Entry<K,V> {
//插入节点的key:
K key;
//插入节点的value:
V value;
//插入节点的左子节点:
java.util.TreeMap.Entry left = null;
//插入节点的右子节点:
java.util.TreeMap.Entry right = null;
//插入节点的父节点:
java.util.TreeMap.Entry parent;
//插入节点默认的颜色:
boolean color = BLACK;
//Entry对象的构造函数:
Entry(K key, V value, java.util.TreeMap.Entry parent) {
this.key = key;
this.value = value;
this.parent = parent;
}
public K getKey() {
return key;
}
public V getValue() {
return value;
}
public V setValue(V value) {
V oldValue = this.value;
this.value = value;
return oldValue;
}
public boolean equals(Object o) {
if (!(o instanceof Map.Entry))
return false;
Map.Entry e = (Map.Entry)o;
return valEquals(key,e.getKey()) && valEquals(value,e.getValue());
}
public int hashCode() {
int keyHash = (key==null ? 0 : key.hashCode());
int valueHash = (value==null ? 0 : value.hashCode());
return keyHash ^ valueHash;
}
public String toString() {
return key + "=" + value;
}
}
- TreeMap构造函数
与HashMap不同,TreeMap底层不是数组结构,成员变量中并没有数组,而是用根节点root来替代,所有的操作都是通过根节点来进行的。
public class TreeMap<K,V>
extends AbstractMap<K,V>
implements NavigableMap<K,V>, Cloneable, java.io.Serializable {
//自定义的比较器:
private final Comparatorsuper K> comparator;
//红黑树的根节点:
private transient java.util.TreeMap.Entry root = null;
//集合元素数量:
private transient int size = 0;
//对TreeMap操作的数量:
private transient int modCount = 0;
//无参构造方法:comparator属性置为null
//代表使用key的自然顺序来维持TreeMap的顺序,这里要求key必须实现Comparable接口
public TreeMap() {
comparator = null;
}
//带有比较器的构造方法:初始化comparator属性;
public TreeMap(Comparatorsuper K> comparator) {
this.comparator = comparator;
}
//带有map的构造方法:
//同样比较器comparator为空,使用key的自然顺序排序
public TreeMap(Map m) {
comparator = null;
putAll(m);
}
//带有SortedMap的构造方法:
//根据SortedMap的比较器来来维持TreeMap的顺序
public TreeMap(SortedMap m) {
comparator = m.comparator();
try {
buildFromSorted(m.size(), m.entrySet().iterator(), null, null);
} catch (java.io.IOException cannotHappen) {
} catch (ClassNotFoundException cannotHappen) {
}
}
}
- TreeMap元素添加
将新增节点的key--value插入到TreeMap当中,在上文中我们已经通过图文的形式介绍了新增的流程,如果你还不明白,可以结合源码进行理解;
首先找到新增节点的位置,其次在判断TreeMap是否处于平衡状态,若不平衡,则对节点进行着色、旋转操作;
//插入key-value:
public V put(K key, V value) {
//根节点赋值给t:
java.util.TreeMap.Entry t = root;
//如果根节点为null,则创建第一个节点,根节点
if (t == null) {
//对传入的元素进行比较,若TreeMap没定义了Comparator,则验证传入的元素是否实现了Comparable接口;
compare(key, key);
//根节点赋值:
root = new java.util.TreeMap.Entry<>(key, value, null);
//长度为1:
size = 1;
//修改次数+1
modCount++;
//直接返回:此时根节点默认为黑色
return null;
}
//如果根节点不为null:
int cmp;
java.util.TreeMap.Entry parent;
Comparator super K> cpr = comparator;
//判断TreeMap中自定义比较器comparator是否为null:
if (cpr != null) {
// do while循环,查找新插入节点的父节点:
do {
// 记录上次循环的节点t,首先将根节点赋值给parent:
parent = t;
//利用自定义比较器的比较方法:传入的key跟当前遍历节点比较:
cmp = cpr.compare(key, t.key);
//判断结果小于0,处于父节点的左边
if (cmp < 0)
t = t.left;
else if (cmp > 0)
//判断结果大于0,处于父节点的右边
t = t.right;
else
//判断结果等于0,为当前节点,覆盖原有节点处的value:
return t.setValue(value);
// 只有当t为null,也就是找到了新节点的parent了
} while (t != null);
} else {
//没有自定义比较器:
if (key == null)
//TreeMap不允许插入key为null,抛异常:
throw new NullPointerException();
//将key转换为Comparable对象:若key没有实现Comparable接口,此处会报错
Comparable super K> k = (Comparable super K>) key;
//同上:寻找新增节点的父节点:
do {
parent = t;
cmp = k.compareTo(t.key);
if (cmp < 0)
t = t.left;
else if (cmp > 0)
t = t.right;
else
return t.setValue(value);
} while (t != null);
}
//构造新增节点对象:
java.util.TreeMap.Entry e = new java.util.TreeMap.Entry<>(key, value, parent);
//根据之前的比较结果,判断新增节点是在父节点的左边还是右边
if (cmp < 0)
// 如果新节点key的值小于父节点key的值,则插在父节点的左侧
parent.left = e;
else
// 如果新节点key的值大于父节点key的值,则插在父节点的右侧
parent.right = e;
//核心方法:插入新的节点后,为了保持红黑树平衡,对红黑树进行调整
fixAfterInsertion(e);
size++;
modCount++;
return null;
}
//对插入的元素比较:若TreeMap没有自定义比较器,则调用调用默认自然顺序比较,要求元素必须实现Comparable接口;
//若自定义比较器,则用自定义比较器对元素进行比较;
final int compare(Object k1, Object k2) {
return comparator==null ? ((Comparable super K>)k1).compareTo((K)k2)
: comparator.compare((K)k1, (K)k2);
}
//核心方法:维护TreeMap平衡的处理逻辑;(回顾上面的图文描述)
private void fixAfterInsertion(java.util.TreeMap.Entry x) {
//首先将新插入节点的颜色设置为红色
x.color = RED;
//TreeMap是否平衡的重要判断,当不在满足循环条件时,代表树已经平衡;
//x不为null,不是根节点,父节点是红色(三者均满足才进行维护):
while (x != null && x != root && x.parent.color == RED) {
//节点x的父节点 是 x祖父节点的左孩子:
if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {
//获取x节点的叔叔节点y:
java.util.TreeMap.Entry y = rightOf(parentOf(parentOf(x)));
//叔叔节点y是红色:
if (colorOf(y) == RED) {
//将x的父节点设置黑色:
setColor(parentOf(x), BLACK);
//将x的叔叔节点y设置成黑色:
setColor(y, BLACK);
//将x的祖父节点设置成红色:
setColor(parentOf(parentOf(x)), RED);
//将x节点的祖父节点设置成x(进入了下一次判断):
x = parentOf(parentOf(x));
} else {
//叔叔节点y不为红色:
//x为其父节点的右孩子:
if (x == rightOf(parentOf(x))) {
x = parentOf(x);
rotateLeft(x);
}
setColor(parentOf(x), BLACK);
setColor(parentOf(parentOf(x)), RED);
//右旋:
rotateRight(parentOf(parentOf(x)));
}
} else {
//节点x的父节点 是x祖父节点的右孩子:
//获取x节点的叔叔节点y:
java.util.TreeMap.Entry y = leftOf(parentOf(parentOf(x)));
//判断叔叔节点y是否为红色:
if (colorOf(y) == RED) {
setColor(parentOf(x), BLACK);12
setColor(y, BLACK);5
setColor(parentOf(parentOf(x)), RED);10
x = parentOf(parentOf(x));
} else {
if (x == leftOf(parentOf(x))) {
x = parentOf(x);
rotateRight(x);
}
setColor(parentOf(x), BLACK);
setColor(parentOf(parentOf(x)), RED);
//左旋:
rotateLeft(parentOf(parentOf(x)));
}
}
}
root.color = BLACK;
}
//获取节点的颜色:
private static boolean colorOf(java.util.TreeMap.Entry p) {
//节点为null,则默认为黑色;
return (p == null ? BLACK : p.color);
}
//获取p节点的父节点:
private static java.util.TreeMap.Entry parentOf(java.util.TreeMap.Entry p) {
return (p == null ? null: p.parent);
}
//对节点进行着色,TreeMap使用了boolean类型来代表颜色(true为红色,false为黑色)
private static void setColor(java.util.TreeMap.Entry p, boolean c){
if (p != null)
p.color = c;
}
//获取左子节点:
private static java.util.TreeMap.Entry leftOf(java.util.TreeMap.Entry p) {
return (p == null) ? null: p.left;
}
//获取右子节点:
private static java.util.TreeMap.Entry rightOf(java.util.TreeMap.Entry p) {
return (p == null) ? null: p.right;
}
//左旋:
private void rotateLeft(java.util.TreeMap.Entry p) {
if (p != null) {
java.util.TreeMap.Entry r = p.right;
p.right = r.left;
if (r.left != null)
r.left.parent = p;
r.parent = p.parent;
if (p.parent == null)
root = r;
else if (p.parent.left == p)
p.parent.left = r;
else
p.parent.right = r;
r.left = p;
p.parent = r;
}
}
//右旋:
private void rotateRight(java.util.TreeMap.Entry p) {
if (p != null) {
java.util.TreeMap.Entry l = p.left;
p.left = l.right;
if (l.right != null) l.right.parent = p;
l.parent = p.parent;
if (p.parent == null)
root = l;
else if (p.parent.right == p)
p.parent.right = l;
else p.parent.left = l;
l.right = p;
p.parent = l;
}
}
- TreeMap元素获取
TreeMap底层是红黑树结构,而红黑树本质是一颗二叉查找树,所以在获取节点方面,使用二分查找算法性能最高;
//通过key获取对应的value:
public V get(Object key) {
//获取TreeMap中对应的节点:
java.util.TreeMap.Entry p = getEntry(key);
//获取节点的值:
return (p==null ? null : p.value);
}
//通过key获取Entry对象:
final java.util.TreeMap.Entry getEntry(Object key) {
//TreeMap自定义比较器不为空,使用自定义比较器对象来获取节点:
if (comparator != null)
//获取节点:
return getEntryUsingComparator(key);
//如果key为null,则抛出异常,TreeMap中不允许存在为null的key:
if (key == null)
throw new NullPointerException();
//将传入的key转换成Comparable类型,传入的key必须实现Comparable接口
Comparablesuper K> k = (Comparablesuper K>) key;
//获取根节点:
java.util.TreeMap.Entry p = root;
// 使用二分查找方式,首先判断传入的key与根节点的key哪个大:
while (p != null) {
//传入的key与p节点的key进行大小比较:
int cmp = k.compareTo(p.key);
//传入的key小于p节点的key,则从根的左子树中搜索:
if (cmp < 0)
//左边
p = p.left;
else if (cmp > 0)
//传入的key大于p节点的key,则从根的右边子树中搜索:
//右边
p = p.right;
else
//传入的key等于p节点的key,则直接返回当前节点:
return p;
}
//以上循环没有找对对应的节点,则返回null:
return null;
}
//使用自定义比较器进行元素比较,获取对节点:
final java.util.TreeMap.Entry getEntryUsingComparator(Object key) {
K k = (K) key;
Comparatorsuper K> cpr = comparator;
if (cpr != null) {
java.util.TreeMap.Entry p = root;
while (p != null) {
int cmp = cpr.compare(k, p.key);
if (cmp < 0)
p = p.left;
else if (cmp > 0)
p = p.right;
else
return p;
}
}
return null;
}
- TreeMap元素删除
作者:贾博岩
链接:https://www.jianshu.com/p/2dcff3634326
來源:简书
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。