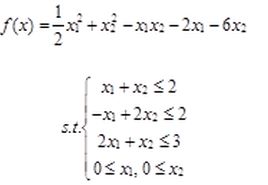Matlab优化工具箱和模拟退火算法

Matlab优化工具箱主要有以下4种求解器：

1.最小值优化

2.多目标最小值优化

3.方程求解器

4.最小二乘（曲线拟合）求解器

 

一.最小值优化：

1.标量最小值优化：使用函数fminbnd

例：对边长为3m的正方形铁板，在4个角处剪去相等的正方形，以制成方形无盖水槽，问如何剪才能使水槽的容积最大？

方程：V=(3-2x)^2x

function f = myfun1(x)
f = -(3-2*x).^2 * x; % 由于fminbnd只能用来计算最小值，所以这里加负号

x = fminbnd(@myfun1,0,1.5)
% x = fminbnd(fun,x1,x2)：返回标量函数fun在条件x1 < x < x2下取最小值时自变量x的值
y= -myfun1(x)    % 调用myfun1函数来计算水槽的最大容积

2.无约束最小值优化:使用函数fminunc和fminsearch

例：求函数f(x)=3x1^2+2x1x2+x2^2最小值

function f = myfun2(x)
f = 3*x(1)^2 + 2*x(1)*x(2) + x(2)^2;    %  目标函数

x0 = [1,1];   % 初始值，可以是标量，向量，矩阵，即从这个值开始找，不熟悉的话可以多试几次，取最优的
[x,fval] = fminunc(@myfun2,x0) % x为自变量，fval为函数值

例：求banana方程的最小值（banana方程：f(x)=100(x2-x1^2)^2+(a-x1)^2，在指定a的情况下求这个方程的最小值）

a=3;
banana = @(x)100*(x(2)-x(1)^2)^2+(a-x(1))^2; % 快速获得函数句柄
options = optimset('Display','iter','PlotFcns',@optimplotfval); % 设置一些参数，将Display参数设置为'iter'，利用optimplotfval来进行画图，'PlotFcns'是画图参数
[x,fval,exitflag,output] = fminsearch(banana, [-1.2, 1], options) % exitflag退出标志，程序运行结束的信息，output是一些输出信息
% 也可以这样（不加TolX的话）
% [x,fval,exitflag,output] = fminsearch(banana, [-1.2, 1], ...
   optimset('TolX',1e-8,'Display','iter','PlotFcns',@optimplotfval))      
%  optimset('TolX',1e-8)用来设置算法终止误差，即设置精度，到这个精度就可以停了

3.线性规划：使用linprog函数

例：求如下函数的最小值

f = [-5; -4; -6];         %  用矩阵表示目标函数
A = [1  -1  1
      3   2  4
      3   2  0];           %  用矩阵形式表示约束条件系数，注意换行也表示;
b = [20; 42; 30];      %  约束条件
lb = zeros(3,1);       %  下界约束
[x,fval,exitflag,output,lambda] = linprog(f,A,b,[],[],lb)
% "[] []"表示的是等式约束，这里没有等式，所以用空矩阵，lb后面还可以加上界约束，但没有，所以可以省略
% Lambda保存的一些约束信息，Lambda域中向量里的非零元素可以反映出求解过程中的主动约束。在本例的结果中可以看出，第2个和第3个不等式约束（lambda.ineqlin）和第1个下界约束（lambda.lower）是主动约束

二次规划：使用quadprog函数

例：求下面函数的最小值

首先将方程写成矩阵形式

（x的指数为2）

H = [1 -1; -1 2];
f = [-2; -6];
A = [1 1; -1 2; 2 1];      %  线性不等式约束
b = [2; 2; 3];               %  线性不等式约束
lb = zeros(2,1);
[x,fval,exitflag,output,lambda] = quadprog(H,f,A,b,[],[],lb)

4.有约束最小值优化：使用函数fmincon

例：求函数f(x)=-x1x2x3的最小值，搜索的起始值为x=[10;10;10]，同时目标函数中的变量要服从以下约束条件：

function f = myfun3(x)
f = -x(1) * x(2) * x(3);

约束条件改为

x0 = [10; 10; 10];    % 求解的起始点
A=[-1 -2 -2;1 2 2];
b=[0;72];
[x,fval] = fmincon(@myfun3,x0,A,b)

5.另外两种极小值优化问题：
半无限问题：fseminf
0-1规划：bintprog
请查阅帮助文档或者其他参考书

二.多目标优化：使用fgoalattain和fminimax函数

例：某工厂因生产需要欲采购一种原材料，市场上这种原材料有两个等级，甲级单价2元/千克，乙级单价1元/千克。要求所花总费用不超过200元，购得原材料总量不少于100千克，其中甲级原材料不少于50千克，问如何确定最好的采购方案。
设x1、x2分别为采购甲级和乙级原材料的数量（千克），要求总采购费用尽量少，总采购重量尽量多，采购甲级原材料尽量多

function f=myfun4(x)
f(1)=2*x(1)+ x(2); % 总花费
f(2)=-x(1)- x(2); % 总重量
f(3)=-x(1); % 甲级材料重量
%注意和下面的一一对应关系

goal=[200 -100 -50];        %  要达到的目标
weight=[2040 -100 -50];       %  各个目标的权重，自己根据经验定
x0=[55 55];                    %  搜索的初始值
%  约束条件
A=[2 1;-1 -1;-1 0];
b=[200 -100 -50]; % 它们的正负需要把方程转化为标准形式才能确定，必须是小于
lb=zeros(2,1);
%  调用fgoalattain函数进行多目标优化
[x,fval,attainfactor,exitflag] =...
fgoalattain(@myfun4,x0,goal,weight,A,b,[],[],lb,[])

fminimax函数用法查阅文档

三.方程组求解：

优化工具箱提供了3个方程求解的函数，其中，“\”算子可用于求解线性方程组Cx=d。当矩阵为n阶方阵时，采用高斯消元法进行求解；如果A不为方阵，则采用数值方法计算方程最小二乘意义上的解。fzero采用数值解法求解非线性方程，fsolve函数则采用非线性最小二乘算法求解非线性方程组

例：求解下面方程组的根，其中包含两个未知数、两个方程

方程组变换

function F = myfun5(x)
F = [2*x(1) - x(2) - exp(-x(1));
      -x(1) + 2*x(2) - exp(-x(2))];

x0 = [-5; -5];                              % 猜测的搜索初始值
options=optimset('Display','iter');       % 输出显示选项设置
[x,fval] = fsolve(@myfun5,x0,options)      % 调用fsolve命令

fzero和“\”自行查阅文档

四.最小二乘及数据拟合：常用函数有\、lsqnonneg、lsqlin、lsqnonlin、lsqcurvefit等

例（伪）：

求超定系统（未知数小于方程数）C·x = d的最小二乘解，约束条件为A·x≤b，lb≤x≤ub（具体的系数矩阵、边界条件如下所示）
首先输入系数矩阵和上下边界

C = [0.9501    0.7620    0.6153    0.4057
    0.2311    0.4564    0.7919    0.9354
    0.6068    0.0185    0.9218    0.9169
    0.4859    0.8214    0.7382    0.4102
    0.8912    0.4447    0.1762    0.8936];
d = [0.0578
    0.3528
    0.8131
    0.0098
    0.1388];
A =[0.2027    0.2721    0.7467    0.4659
    0.1987    0.1988    0.4450    0.4186
    0.6037    0.0152    0.9318    0.8462];
b =[0.5251
    0.2026
    0.6721];
lb = -0.1*ones(4,1);
ub = 2*ones(4,1);

[x,resnorm,residual,exitflag,output,lambda] = ...
    lsqlin(C,d,A,b,[],[],lb,ub);
% resnorm=norm(C*x-d)^2，即2-范数
% residual=C*x-d，即残差
x,lambda.ineqlin,lambda.lower,lambda.upper   %  查看计算的结果

其它函数请自行查阅文档

模拟退火：

dejong5fcn    % 优化测试函数
fun = @dejong5fcn;    % 目标函数
[x,fval] = simulannealbnd(fun,[0 0])    % 目标函数、初始点

% 如果有绘图
options = saoptimset('PlotFcns',{@saplotbestx,@saplotbestf,@saplotx,@saplotf});
%第一个绘图函数是最优的函数值对应的x点，第二个是最优的函数值，第三个是当前的x，第四个是当前的函数值
% 如果有上下限约束
x0 = [0,0];
lb = [-64,-64];
ub = [64,64];
x = simulannealbnd(fun,x0,lb,ub,options)

例：

求min f(x) = (4 - 2.1*x1^2 + x1^4/3)*x1^2 + x1*x2 + (-4 + 4*x2^2)*x2^2
写成函数形式
 

function y = simple_objective(x)
   y = (4 - 2.1*x(1)^2 + x(1)^4/3)*x(1)^2 + x(1)*x(2) + (-4 + 4*x(2)^2)*x(2)^2;

ObjectiveFunction = @simple_objective;
X0 = [0.5 0.5];   % 初始点
[x,fval,exitFlag,output] = simulannealbnd(ObjectiveFunction,X0)

% 如果有上下限约束
lb = [-64 -64];
ub = [64 64];
[x,fval,exitFlag,output] = simulannealbnd(ObjectiveFunction,X0,lb,ub);

例：

求min f(x) = (a - b*x1^2 + x1^4/3)*x1^2 + x1*x2 + (-c + c*x2^2)*x2^2

写成函数形式

function y = parameterized_objective(x,a,b,c)
   y = (a - b*x(1)^2 + x(1)^4/3)*x(1)^2 + x(1)*x(2) + (-c + c*x(2)^2)*x(2)^2;

a = 4; b = 2.1; c = 4;    % define constant values
ObjectiveFunction = @(x) parameterized_objective(x,a,b,c);
X0 = [0.5 0.5];
[x,fval] = simulannealbnd(ObjectiveFunction,X0)