寒假思维训练day19

 更新一道div3的F  和   做出来过的一道类似这个F的  icpc铜牌题, 美赛以后的第一篇。

 题目链接，有需自取：

div3 F链接：Problem - F - Codeforces

icpc Asia macau 铜牌题 Problem - K - Codeforces

---

摘要

Part1  div3 F 的题意、题解、代码(C++) 

Part2  2021 icpc macau 铜牌题 的题意、题解、代码(C++) 

Part3 回顾求倍增dp求Lca  和   kruskal  和   启发式合并优化的并查集

---

Part1 K. Link-Cut Tree: 

1、题意：

给定一个点数为，边数为的无向图，第i条边的长度是，不包含自环和重边，图不一定连通，求出图中边权之和最小的简单环，简单环至少包含3个顶点。多组测试数据，n，m总和不大于, 并且。如果图中不存在简单环就输出，否则输出按递增顺序排列的答案简单环边的索引。

2、题解:

我们知道边是，由等比数列公式易得，我们欲想找到图中最小简单环不妨先对总体求一颗最小生成树，再遍历没使用过的边，找到第一条边所在的环就是题目中要求的最小环，我们记录这条边上的两点，因为边权是递增的并且每个都不同，我们反证一下，假设不是第一条边，我们设第一条边是，第二条边必然满足，显然它一定大于所有边累加之和，根据kruskal我们可以知道未选上的边的两点一定能通过比它边权更小的边合并到树中。

得证，显然如果没找到这样的边，原图就是一颗树，无解，反之，对于找到的边我们再加到生成树中，我们就得到了一颗基环树，再从记录好的边上的其中一点出发， 知道路径可以返回该点，记录边的编号，最后得到答案。

3、代码(C ++) 

#include 
#define int long long 
using namespace std;
const int N = 2e5; 
const int inf = 0x3f3f3f3f; 
int n, m; 
int h[N], ne[N << 1], e[N << 1], w[N << 1], idx; 
int p[N], cnt[N]; 
bool st[N]; 
int s, ed;  
int q[N], o;
bool flag;

struct edge {
    int a, b, c; 
}eg[N << 1]; 
void add(int a, int b, int c) {
    e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx ++; 
}
int find(int x) {
    if(x != p[x]) p[x] = find(p[x]); 
    return p[x]; 
}

void dfs(int u, int fa) {
    if(st[u]) {
        if(u == s) flag = 1; 
        return; 
    }
    st[u] = 1; 
    for(int i = h[u]; ~i; i = ne[i]) {
        int j = e[i]; 
        if(j == fa) continue; 
        if(u == s && j == ed) continue; 
        q[++ o] = w[i]; 
        dfs(j, u); 
        if(flag) return; 
        -- o; 
    }
}
void solve() {
    idx = 0; 
    cin >> n >> m; 
    for(int i = 0; i <= n; i ++ ) h[i] = -1, p[i] = i, cnt[i] = 1;  
    for(int i = 1; i <= m; i ++ ) {
        st[i] = 0;
        int u, v; 
        cin >> u >> v;
        eg[i] = {u, v, i}; 
        if(find(u) == find(v)) continue; 
        if(cnt[find(u)] >= cnt[find(v)]) {
            cnt[find(u)] += cnt[find(v)]; 
            p[find(v)] = find(u); 
        }
        else {
            cnt[find(v)] += cnt[find(u)]; 
            p[find(u)] = find(v); 
        }
        add(u, v, i), add(v, u, i); 
        st[i] = 1; 
    }
    
    s = -1, ed = -1; 
    for(int i = 1; i <= m; i ++ ) {
        if(st[i]) continue; 
        int a = eg[i].a, b = eg[i].b, c = eg[i].c; 
        add(a, b, c), add(b, a, c);  
        s = a, ed = b; 
        break;    
    }
    if(s == -1) {
        cout << -1 << endl;
        return; 
    }
    
    for(int i = 1; i <= n; i ++ ) st[i] = 0; 
    o = 0; 
    flag = 0; 
    
    dfs(s, -1); 
    
    sort(q + 1, q + 1 + o); 
    for(int i = 1; i <= o; i ++ ) cout << q[i] << " \n"[i == o]; 
}
signed main() {
    ios::sync_with_stdio(false); 
    cin.tie(0); 
    cout.tie(0); 
    int ts; 
    cin >> ts; 
    while(ts -- ) 
        solve(); 
    
    return 0; 
}

---

Part2 F. Microcycle

1、题意：

给定一个点数为n，边数为m的无向图，没有重边和自环，图不一定连通，对于给定的图找到

一个最有简单环，使得环上最小边权小于等于图上其它简单环的环上最小边权，输出环上最小边权和换上点数，再按环的顺序输出点，一定有解。

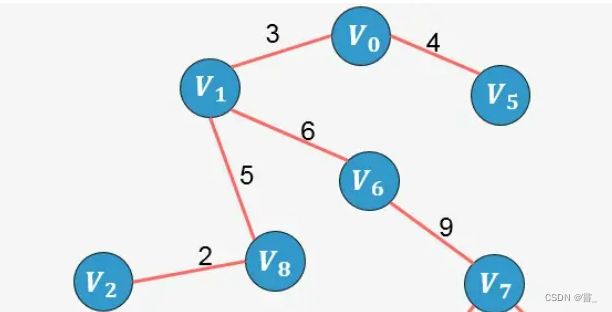
2、题解：

我们有了上一题的基础，我们不妨对原图求一个最小生成树，这样我们得到了一个最小生成森林，我们遍历未被使用的边，此处一定是在一个连通块的点，我们不妨求一下这个环的最小边权，那怎么求呢，我们观察一下树上的两点V2和V7, 我们可以看到它们之间的最小值是从自己位置到最近公共祖先取min, 我们在维护Lca的同时维护一个最小值就可以的求出任意两点间环的最小边权。

最后我们找到那条边，再通过Lca找点输出(具体见代码)。

3、代码(C ++)

#include 
#define int long long 
using namespace std; 
constexpr int N = 2e5 + 10, inf = 0x3f3f3f3f; 
int n, m;
int h[N], e[N << 1], ne[N << 1], w[N << 1], idx; 
int p[N], cnt[N]; 
int dep[N], fa[N][19], dis[N][19]; 
bool st[N]; 
struct edge {
    int a, b, c;
    bool operator< (const edge& W) const {
        return c < W.c;
    };
}eg[N << 1]; 
void add(int a, int b, int c) {
    e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx ++; 
}
inline int find(int x) {
    if(x != p[x]) p[x] = find(p[x]); 
    return p[x]; 
}
int q[N]; 
void bfs(int root) 
{
    int hh = 0, tt = -1;
    dep[root] = 1; 
    fa[root][0] = 0;
    q[++ tt] = root; 
    while(hh <= tt) 
    {
        int t = q[hh ++]; 
        for(int i = h[t]; ~i; i = ne[i]) 
        {
            int j = e[i]; 
            if(dep[j] > dep[t] + 1)
            {
                dep[j] = dep[t] + 1; 
                q[++ tt] = j; 
                fa[j][0] = t; 
                dis[j][0] = w[i]; 
                for(int k = 1; k <= 18; k ++ ) 
                    fa[j][k] = fa[fa[j][k - 1]][k - 1],
                    dis[j][k] = min(dis[j][k - 1],dis[fa[j][k - 1]][k - 1]); 
            }
        }
    }
}
int Lca_Distance(int a, int b) {
    int ans = inf; 
    if(dep[a] <= dep[b]) swap(a, b); 
    for(int i = 18; i >= 0; i -- ) 
        if(dep[fa[a][i]] >= dep[b]) {
            ans = min(ans, dis[a][i]); 
            a = fa[a][i]; 
        }
    if(a == b) return ans; 
    for(int i = 18; i >= 0; i -- ) 
        if(fa[a][i] != fa[b][i]) {
            ans = min(ans, dis[a][i]), ans = min(ans, dis[b][i]); 
            a = fa[a][i], b = fa[b][i]; 
        }  
    ans = min(ans, dis[b][0]), ans = min(ans, dis[a][0]); 
    return ans; 
}
int Lca(int a, int b) {
    if(dep[a] <= dep[b]) swap(a, b); 
    for(int i = 18; i >= 0; i -- ) 
        if(dep[fa[a][i]] >= dep[b]) 
            a = fa[a][i]; 
    if(a == b) return a;  
    for(int i = 18; i >= 0; i -- ) 
        if(fa[a][i] != fa[b][i]) 
            a = fa[a][i], b = fa[b][i]; 
    return fa[a][0]; 
}

int q1[N], q2[N], c1, c2; 
void solve() {
    idx = 0; 
    scanf("%lld%lld", &n, &m); 
    for(int i = 0; i <= n; i ++ ) 
        for(int j = 0; j <= 18; j ++ ) 
            dis[i][j] = inf, fa[i][j] = 0; 
    for(int i = 0; i <= n; i ++ ) h[i] = -1, cnt[i] = 1, p[i] = i, dep[i] = inf;
    dep[0] = 0; 
    for(int i = 1; i <= m; i ++ ) {
        st[i] = 0; 
        int a, b, c; 
        scanf("%lld%lld%lld", &a,&b,&c);
        eg[i] = {a, b, c}; 
    }
    sort(eg + 1, eg + 1 + m); 
    for(int i = 1; i <= m; i ++ ) {
        int a = eg[i].a, b = eg[i].b, c = eg[i].c;
        if(find(a) == find(b)) continue;
        if(cnt[find(a)] >= cnt[find(b)]) {
            cnt[find(a)] += cnt[find(b)]; 
            p[find(b)] = find(a); 
        }
        else {
            cnt[find(b)] += cnt[find(a)]; 
            p[find(a)] = find(b); 
        }
        st[i] = 1; 
        add(a, b, c), add(b, a, c); 
    }
    for(int i = 1; i <= n; i ++ ) 
        if(find(i) == i && cnt[i] >= 3) bfs(i); 
    int s, ed, res = inf; 
    for(int i = 1; i <= m; i ++ ) {
        if(st[i]) continue;
        int a = eg[i].a, b = eg[i].b, c = eg[i].c;
        int v = Lca_Distance(a, b); 
        if(v < res) {
            res = v; 
            s = a, ed = b; 
        } 
    }    
    int Lc = Lca(s, ed); 
    c1 = 0, c2 = 0; 
    while(s && dep[s] >= dep[Lc]) q1[++ c1] = s, s = fa[s][0]; 
    while(ed && dep[ed] > dep[Lc]) q2[++ c2] = ed, ed = fa[ed][0];
    printf("%lld %lld\n", res, c1 + c2); 
    for(int i = 1; i <= c1; i ++ ) printf("%lld ",q1[i]); 
    for(int i = c2; i >= 1; i -- ) printf("%lld ", q2[i]); 
    printf("\n"); 
}
signed main() {
    int ts; 
    scanf("%lld",&ts); 
    while(ts -- ) solve(); 
}

---

Part3  算法回顾：

1、倍增Lca模板

#include  
#include  
#include   
#include  
using namespace std; 
const int N = 4e4 + 10, M = N * 2, INF = 0x3f3f3f3f; 
int n, m, k;
int fa[N][16], dist[N];
int h[N], e[M], ne[M], idx; 
int root; 
int q[N]; 
void add(int a, int b) 
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++; 
}
void bfs(int rot) 
{
    int hh = 0, tt = -1; 
    memset(dist, 0x3f, sizeof dist); 
    dist[0] = 0, dist[rot] = 1; 
    fa[rot][0] = 0;
    q[++ tt] = rot; 
    while(hh <= tt) 
    {
        int t = q[hh ++]; 
        for(int i = h[t]; ~i; i = ne[i]) 
        {
            int j = e[i]; 
            if(dist[j] > dist[t] + 1)
            {
                dist[j] = dist[t] + 1; 
                q[++ tt] = j; 
                fa[j][0] = t; 
                for(int k = 1; k <= 15; k ++ ) 
                    fa[j][k] = fa[fa[j][k - 1]][k - 1]; 
            }
        }
    }
}
int lca(int a, int b) 
{
    if(dist[a] <= dist[b]) swap(a, b); 
    for(int i = 15; i >= 0; i -- ) 
        if(dist[fa[a][i]] >= dist[b]) 
            a = fa[a][i]; 
    if(a == b) return a; 
    for(int i = 15; i >= 0; i -- ) 
        if(fa[a][i] != fa[b][i]) 
            a = fa[a][i], b = fa[b][i]; 
    return fa[a][0]; 
}
int main() 
{
    memset(h, -1, sizeof h); 
    cin >> n; 
    for(int i = 1; i <= n; i ++ ) 
    {
        int a, b; 
        cin >> a >> b; 
        if(b == -1) root = a; 
        else add(a, b), add(b, a); 
    }
    bfs(root); 
    cin >> m; 
    while(m --) 
    {
        int x, y; 
        cin >> x >> y; 
        int Fa = lca(x, y); 
        if(Fa == x) puts("1");
        else if(Fa == y) puts("2"); 
        else puts("0"); 
    }
    return 0; 
}

2、kruskal模板：

#include
#include 
#include 
using namespace std; 
const int N = 2e5 + 10, M = 1e5 + 10, INF = 0x3f3f3f3f;  
int n, m; 
int p[M]; 
struct edg
{
    int a, b, w;
    bool operator < (const edg &W) const 
    {
        return w < W.w; 
    }; 
}es[N];  
int find(int x) 
{
    if(p[x] != x) p[x] = find(p[x]); 
    return p[x]; 
}
int kurstal() 
{
    sort(es, es + m); 
    for(int i = 1; i <= n; i ++) p[i] = i; 
    int res = 0, cnt = 0;  
    for(int i = 0; i < m; i ++) 
    {
        int a = find(es[i].a), b = find(es[i].b), w = es[i].w; 
        if(a != b) 
        {
            p[a] = b; 
            res += w; 
            cnt ++; 
        }
    }
    if(cnt < n - 1 ) return INF; 
    return res; 
}
int main() 
{
    scanf("%d%d", &n, &m); 
    for(int i = 0; i < m; i ++) 
    {
        int x, y, z; 
        scanf("%d%d%d", &x, &y, &z); 
        es[i] = {x, y, z}; 
    }
    int t = kurstal(); 
    if(t == INF) puts("impossible"); 
    else printf("%d\n", t);
    return 0; 
}

3、大块合并小块，启发式合并并查集

inline int find(int x) {
    if(x != p[x]) p[x] = find(p[x]); 
    return p[x]; 
}
    
if(find(a) == find(b)) 
    continue;
if(cnt[find(a)] >= cnt[find(b)]) {
    cnt[find(a)] += cnt[find(b)]; 
    p[find(b)] = find(a); 
}
else {
    cnt[find(b)] += cnt[find(a)]; 
    p[find(a)] = find(b); 
}

 

---