树形dp整理及入门

树形dp常用作解三种题：

1.最大独立子集

最大独立子集的定义是，对于一个树形结构，所有的孩子和他们的父亲存在排斥，也就是如果选取了某个节点，那么会导致不能选取这个节点的所有孩子节点。

询问是让你给出这颗树的最大独立子集的大小。思路：对于任意一个节点，他都有两种选择：

A . 选择：A选择，那么他的孩子必定不能要，此时对于A和A的孩子们来说，能构成的最大独立子集是1+∑A.son.notcome。

B . 不选择：A不选择，那么他的孩子们可来可不来，此时对于A和A的孩子们来说，能构成的最大独立子集是

for i 1->son.size  father.notcome+=max(son.notcome,son.come);

当然可以在这基础上加以变化，比如给点设置权值，要你求得这个最大独立子集是满足有最大权值和的。

 

2.树的重心

树的重心定义为，当将节点x去掉后，树所形成的各个联通块的节点个数最少。

那么显而易见，我们需要对每一个节点维护两个值。一个是包含他在内的所有节点的个数【用来返回给他们的‘父亲’】，一个是这个点的最大子树所含有的节点个数。

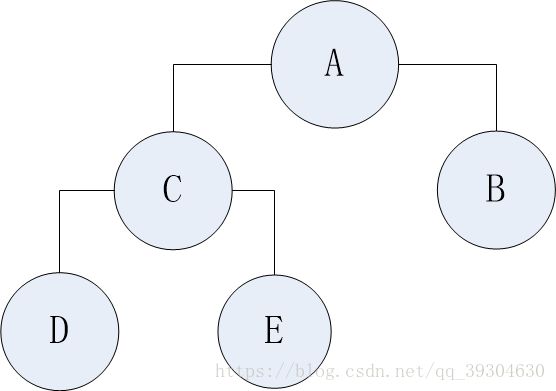
虽然说是一棵树，但其实本身应该作为无根树考虑，也就是，父亲并不是严格意义上的父亲，如下图：

在考虑C的时候，我们应该把C当成整棵树的根，因此C有三棵子树，但是在真正实现的时候，这追踪方法下的复杂度是O(n^2)的，并不现实。时机上，根据树的性质我们可以先求出C在遍历时的孩子个数sum，往上走的分支只要用n-sum就得到了。我们要求的节点就是拥有最大子树的节点。

 

3.树的直径

树的直径定义为一棵树上两个节点间的路径长度的最大值。

一般思路：一棵树上n个节点，两两配对可以组成n*(n-1)/2，所以我们可以对n个节点都做一次dfs，并求得最长的路径，这样这些配对必定会在dfs的过程中求出，这样复杂度就是O(n*n)，n次遍历，每次都要遍历除了自己以外的n-1个节点。

进阶思路：我们以任意一个节点作为根节点，得到他的最高子树的叶子节点，那么这个节点必定是其中的一个节点，在以这个点为起点，dfs得到和他最大距离的点，这条路就是最长路径，复杂度为O(n)，两次dfs。

树形dp：我们以任意一个点为根，向下进行遍历，而经过这个点的最大路径一定是在他的不同的子树中，因此我们可以记录这个点的各个子树的高度的最大值和次大值。累加即为经过这个节点时的最长路经长度。

疑问：题目并没有限制一个节点只能往下找，同样可以往上找，那为什么不往上找呢。解答：往上找出来的路径必定会经过他的父亲，问题就由经过孩子的最大路径变成了经过父亲的最大路径，问题的本质是没有变的，因为这样找出来的路径，父亲和孩子是相同的，是同时经过父亲和孩子的，也就是同样的问题，那么这个问题归根到底就是经过根的最大路径，所以问题重复了，因此我们不必往上找。

 

树形dp的实现：

对于有根树，可以考虑建树递归，在回溯的时候更新结果。

对于无根树，用vector实现邻接表存储。

存储结构:

A. 无权值

vectorPicture[n+1];

遍历方式为:

void dp(int now,int pre){
    int len=Picture[now].size();
    for(int i=0;i         if(Picture[now][i]==pre)continue;//不能回父亲 否则递归不能结束  会吃尽内存导致程序崩溃抑或是爆栈等
        dp(Picture[now][i],now);
    }
} 

 

下面给出三种类型题目的代码：【注：下面的遍历方式都是默认树节点从1开始的，如从0开始将递归入口search(1,0)修改为search(0,-1)即可】

1.最大独立子集

#include
#include
#include
using namespace std;
vectorNode[1000005];
int Maxsize,n;//最大独立子集大小 

struct returnType{
    int come,notcome;
};

returnType search(int now,int pre){
    returnType fa,son; 
    int len=Node[now].size(),soncome,sonnotcome;
    fa.come=1;//总结点数先算上自身1 
    fa.notcome=0;//最大子树先设置为0 
    for(int i=0;i         if(Node[now][i]==pre){continue;}//不回父亲
        son=search(Node[now][i],now);
        fa.come+=son.notcome;
        fa.notcome+=max(son.come,son.notcome);
    }
    return fa;
}

int main(){
    int u,v;
    scanf("%d",&n);
    for(int i=1;i         scanf("%d%d",&u,&v);
        Node[u].push_back(v);
        Node[v].push_back(u);
    }
    returnType father=search(1,0);
    printf("%d",max(father.come,father.notcome));
    return 0;
}
 

 

2.树的重心

#include
#include
#include
using namespace std;
int num[1000005],size[1000005],n;//num ：节点数   size ：最大子树的节点数
vectorNode[1000005];
int target,Maxsize;//重心与最大子树尺寸 

void search(int now,int pre){
    int len=Node[now].size(),result,rest;
    num[now]=1;//总结点数先算上自身1 
    size[now]=0;//最大子树先设置为0 
    for(int i=0;i         if(Node[now][i]==pre){continue;}//不回父亲
        search(Node[now][i],now);
           size[now]=max(size[now],num[Node[now][i]]);
        num[now]+=num[Node[now][i]]; 
    }
    rest=n-num[now];
    size[now]=max(size[now],rest);
       if(Maxsize            Maxsize=size[now];
           target=now;
    }
}

int main(){
    int u,v;
    scanf("%d",&n);
    for(int i=1;i         scanf("%d%d",&u,&v);
        Node[u].push_back(v);
        Node[v].push_back(u);
    }
    search(1,0);
    printf("%d",target);
    return 0;
}

哇，有没有感觉num和size数组是在太耗内存了。没关系，咱们有奇技淫巧。

#include
#include
#include
using namespace std;
vectorNode[1000005];
int n,target,Maxsize;//重心与最大子树尺寸 

struct returnType{
    int size;
    int num;
};

returnType search(int now,int pre){
    returnType fa,son; 
    int len=Node[now].size(),result,rest;
    fa.num=1;//总结点数先算上自身1 
    fa.size=0;//最大子树先设置为0 
    for(int i=0;i         if(Node[now][i]==pre){continue;}//不回父亲
        son=search(Node[now][i],now);
           fa.size=max(fa.size,son.num);
        fa.num=son.num; 
    }
    rest=n-fa.num;
    fa.size=max(fa.size,rest);
       if(Maxsize            Maxsize=fa.size;
           target=now;
    }
    return fa;
}

int main(){
    int u,v;
    scanf("%d",&n);
    for(int i=1;i         scanf("%d%d",&u,&v);
        Node[u].push_back(v);
        Node[v].push_back(u);
    }
    search(1,0);
    printf("%d",target);
    return 0;
}

其实对一个节点来说，只是需要它的孩子们的信息，所以并没有必要开个数组存下来所有的数据。

 

3.树的直径

#include
#include
#include
using namespace std;
int first[1000005],second[1000005];//树形dp求解最长路
vectorNode[1000005];
int longest;
void search(int now,int pre){
    int len=Node[now].size(),result;
    for(int i=0;i         if(Node[now][i]==pre)continue;//不回父亲
        search(Node[now][i],now);
        if(first[Node[now][i]]+1>first[now]){
            second[now]=first[now];
            first[now]=first[Node[now][i]]+1;
        }
        else if(first[Node[now][i]]+1>second[now]){
            second[now]=first[Node[now][i]]+1;
        }
    }
    longest=max(first[now]+second[now],longest);
}

int main(){
    int n,u,v;
    scanf("%d",&n);
    for(int i=1;i         scanf("%d%d",&u,&v);
        Node[u].push_back(v);
        Node[v].push_back(u);
    }
    search(1,0);
    printf("%d",longest+1);
    return 0;
}