吉林大学ACM集训队选拔赛（重现赛）部分题解(ABDFGK)

A777
https://ac.nowcoder.com/acm/contest/5944/A
来源：牛客网

题目描述 
One day, Ks raised a question in this contest.

How many times the digit 7 appears in the integer range of [0, n]?

The answer may be very large, please output the answer modulo 1000000007.


输入描述:
First line contains an integer T  (1≤T≤100), indicating the count of questions.

Each of the following T lines contains one integer n(1≤n≤100000).



输出描述:
Output T lines, one number per line representing the answer.
示例1
输入
复制
10
940948
8
951
8152761
6322168
361892
254312334
8387
277931
56502860
输出
复制
566285
1
285
5870808
3758627
174579
197554663
3479
139247
38850866

思路：
根据第三个样列951输出285.发现285=100+90+95；分别就是百位十位个位出现7的次数，然后就得到一个公式，详细见代码过程，一次处理就行

#include
using namespace std;
const int N=1e6+15;
typedef long long ll;
ll f[N],s[N],a[N],ls[N];
ll mod=1e9+7;
int main()
{
    ll t;
    string str;
    f[0]=1;
    for(int i=1;i<=100000+10;i++)
    {
        f[i]=f[i-1]*10; f[i]%=mod;
    }
    cin>>t;
    while(t--)
    {
        cin>>str;
        ll n=str.length();
        for(int i=0;i<=n;i++)
            a[i+1]=ll(str[i]-'0');
        for(int i=1;i<=n;i++)
        {
            s[i]=s[i-1]*10+a[i];    s[i]%=mod;
        }
        ls[n+1]=0;
        for(int i=n;i>=1;i--)
        {
            ls[i]=f[n-i]*a[i]+ls[i+1];  ls[i]%=mod;
        }
        ll ans=0;
        for(int i=1;i<=n;i++)
        {
            ll op=s[i-1];
            ans=ans+ (op*f[n-i]);
            if(a[i]==7)
            {
                ans+=ls[i+1];
                ans++;
            }
            if(a[i]>7)
                ans=ans+f[n-i];
            ans%=mod;
        }
        cout<<ans<<endl;
    }
    return 0;
}

B subset of five

题目链接

题目描述 点题目链接 ，粘贴过来 太难看了，一个个改就很麻烦
大概意思 就是 给你n个数，你可以选任意个数，但要满足和是5的倍数
输出描述:
Output the maximal sum of S.
示例1
输入
复制
5
2 10 6 3 1
输出
复制
20

思路：首先全部数的和对5取余肯定是[0,1,2,3,4]中的一个，对于0直接输出和
然后对于其中的任意一个数，想办法消去最小的影响就行，如果最后没有符合条件的情况就输出0.

代码：

#include
using namespace std;
const int N=1e6+15;
typedef long long ll;
ll a[N],a1[N],a2[N],a3[N],a4[N];
int main()
{
    ll n,cnt1=0,cnt2=0,cnt3=0,cnt4=0,s=0;
    cin>>n;
    for(int i=1;i<=n;i++)
    {
        cin>>a[i];
        s+=a[i];
        if(a[i]%5==1)
            a1[++cnt1]=a[i];
        if(a[i]%5==2)
            a2[++cnt2]=a[i];
        if(a[i]%5==3)
            a3[++cnt3]=a[i];
        if(a[i]%5==4)
            a4[++cnt4]=a[i];
    }
    if(s%5==0)
    {
        cout<<s<<endl;  return 0;
    }
    sort(a1+1,a1+1+cnt1);
    sort(a2+1,a2+1+cnt2);
    sort(a3+1,a3+1+cnt3);
    sort(a4+1,a4+1+cnt4);

    if(s%5==1)
    {
        ll op=112346789123;
        if(cnt1>=1)
        {
            op=min(op,a1[1]);
        }
        if(cnt2>=3)
        {
            op=min(op,a2[1]+a2[2]+a2[3]);
        }
        if(cnt3>=2)
        {
            op=min(op,a3[1]+a3[2]);
        }
        if(cnt4>=4)
        {
            op=min(op,a4[1]+a4[2]+a4[3]+a4[4]);
        }
        if(cnt2>=1&&cnt4>=1)
        {
            op=min(op,a2[1]+a4[1]);
        }
        if(cnt3>=1&&cnt4>=2)
        {
            op=min(op,a3[1]+a4[1]+a4[2]);
        }
        if(op==1123456789123)
        {
            cout<<"0"<<endl;
        }
        else
        {
            cout<<(s-op)<<endl;
        }
    }
    if(s%5==2)
    {
        ll op=112346789123;
        if(cnt1>=2)
        {
            op=min(op,a1[1]+a1[2]);
        }
        if(cnt2>=1)
        {
            op=min(op,a2[1]);
        }
        if(cnt3>=4)
        {
            op=min(op,a3[1]+a3[2]+a3[3]+a3[4]);
        }
        if(cnt4>=3)
        {
            op=min(op,a4[1]+a4[2]+a4[3]);
        }
        if(cnt1>=1&&cnt3>=2)
        {
            op=min(op,a1[1]+a3[1]+a3[2]);
        }
        if(cnt3>=1&&cnt4>=1)
        {
            op=min(op,a3[1]+a4[1]);
        }
        if(op==1123456789123)
        {
            cout<<"0"<<endl;
        }
        else
        {
            cout<<(s-op)<<endl;
        }
    }
    if(s%5==3)
    {
        ll op=112346789123;
        if(cnt1>=3)
        {
            op=min(op,a1[1]+a1[2]+a1[3]);
        }
        if(cnt2>=4)
        {
            op=min(op,a2[1]+a2[2]+a2[3]+a2[4]);
        }
        if(cnt3>=1)
        {
            op=min(op,a3[1]);
        }
        if(cnt4>=2)
        {
            op=min(op,a4[1]+a4[2]);
        }
        if(cnt1>=1&&cnt2>=1)
        {
            op=min(op,a1[1]+a2[1]);
        }
        if(cnt2>=2&&cnt4>=1)
        {
            op=min(op,a2[1]+a2[2]+a4[1]);
        }
        if(op==1123456789123)
        {
            cout<<"0"<<endl;
        }
        else
        {
            cout<<(s-op)<<endl;
        }
    }
    if(s%5==4)
    {
        ll op=112346789123;
        if(cnt1>=4)
        {
            op=min(op,a1[1]+a1[2]+a1[3]+a1[4]);
        }
        if(cnt2>=2)
        {
            op=min(op,a2[1]+a2[2]);
        }
        if(cnt3>=3)
        {
            op=min(op,a3[1]+a3[2]+a3[3]);
        }
        if(cnt4>=1)
        {
            op=min(op,a4[1]);
        }
        if(cnt1>=2&&cnt2>=1)
        {
            op=min(op,a1[1]+a1[2]+a2[1]);
        }
        if(cnt1>=1&&cnt3>=1)
        {
            op=min(op,a1[1]+a3[1]);
        }
        if(op==1123456789123)
        {
            cout<<"0"<<endl;
        }
        else
        {
            cout<<(s-op)<<endl;
        }
    }
    return 0;
}

D Query Theory I
题目链接

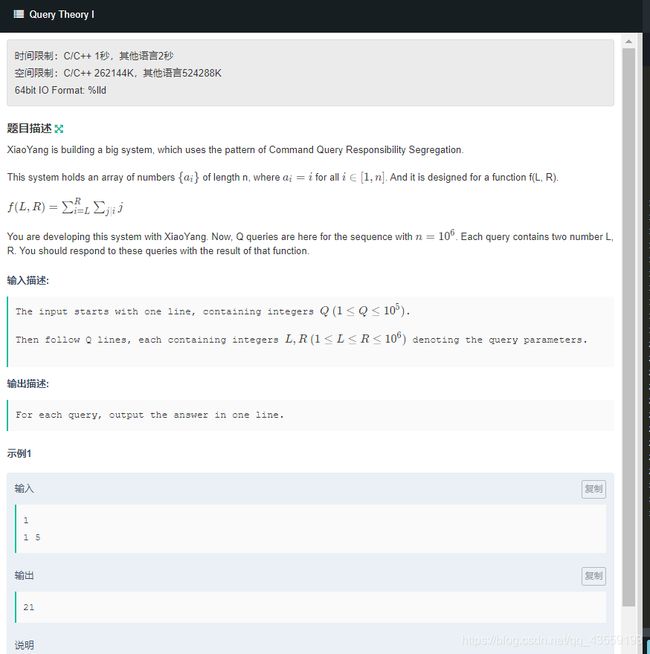
思路 ：题意如图，开数组f[N]，f[x]代表x的贡献，直接倍增筛出来就行。

代码：

#include
using namespace std;
const int N=1e6+15;
typedef long long ll;
bool vis[N];
ll prime[N],f[N];
ll cnt=0;
void Prime()
{
    ll n=1000000;
    for(int i=1;i<=n;i++)
    {
        for(int j=i;j<=n;j+=i)
        {
            f[j]+=i;
        }
    }
    for(int i=1;i<=n;i++)
        f[i]=f[i-1]+f[i];
}
int main()
{
    Prime();
    ll t,l,r;
    cin>>t;
    while(t--)
    {
        cin>>l>>r;
        cout<<(f[r]-f[l-1])<<endl;
    }
    return 0;
}

F EndAs GPA
题面：

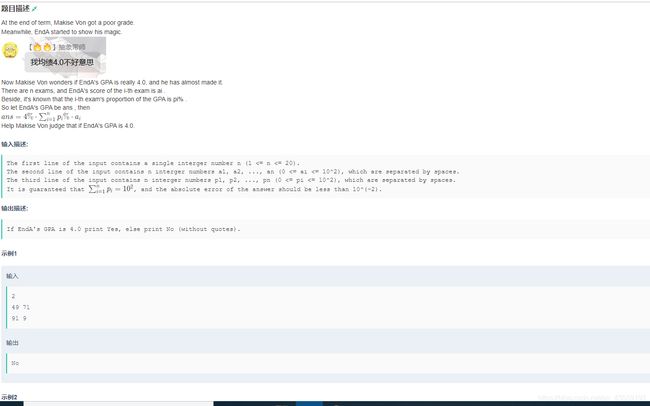
题意直接看题面；
思路：签到题，直接求和判断就行，注意精度。
代码：

#include
using namespace std;
const int N=1e6+15;
typedef long long ll;
ll a[N],b[N];
int main()
{
    ll n,ans=0;
    cin>>n;
    for(int i=1;i<=n;i++)
        cin>>a[i];
    for(int i=1;i<=n;i++)
    {
        cin>>b[i];
        ans=ans+a[i]*b[i];
    }
    if(abs(10000-ans)<=1)
        cout<<"Yes"<<endl;
    else
        cout<<"No"<<endl;
    return 0;
}

G Pair Complex
题面：

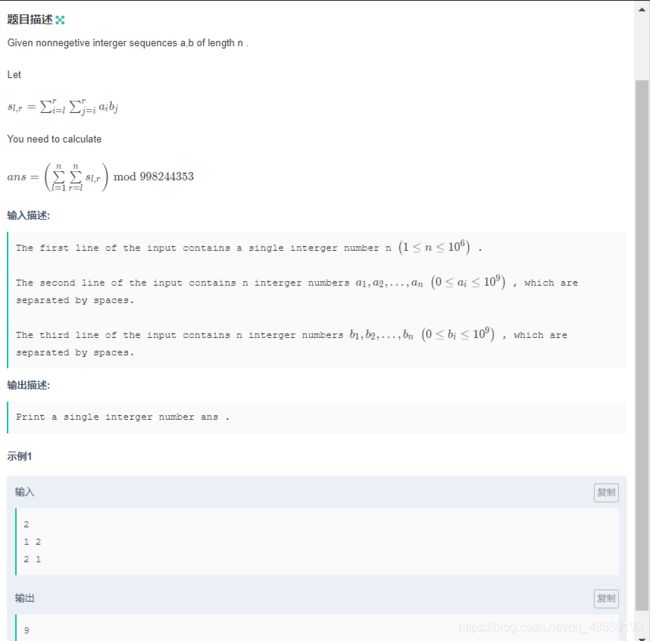
题意直接看图；
思路：手写n=2，n=3的情况
可以发现规律公式，如图

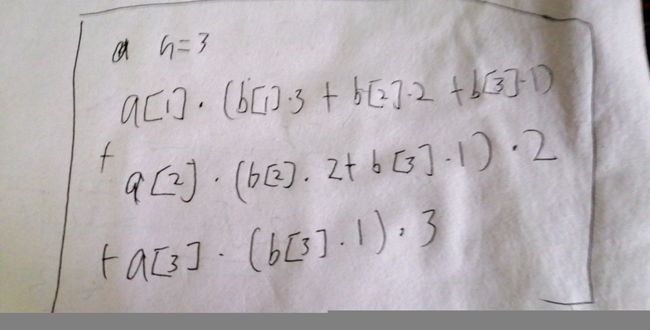
然后直接写就行

代码：

#include
using namespace std;
const int N=1e6+1500;
typedef long long ll;
ll mod=998244353;
ll a[N],b[N],c[N],s[N];
int main()
{
    ll n;
    cin>>n;
    for(int i=1;i<=n;i++)
        scanf("%lld",&a[i]);
    for(int i=1;i<=n;i++)
        scanf("%lld",&b[i]);
    for(int i=1;i<=n;i++)
        c[i]=(b[i]*(n-i+1))%mod;
    for(int i=n;i>=1;i--)
    {
        s[i]=s[i+1]+c[i];   s[i]%=mod;
    }
    ll ans=0;
    for(int i=1;i<=n;i++)
    {
        ll op=a[i]*s[i];    op%=mod;
        op*=i;  op%=mod;
        ans+=op; ans%=mod;
    }
    //cout<
    cout<<ans<<endl;
    return 0;
}

K Dress as women
题面

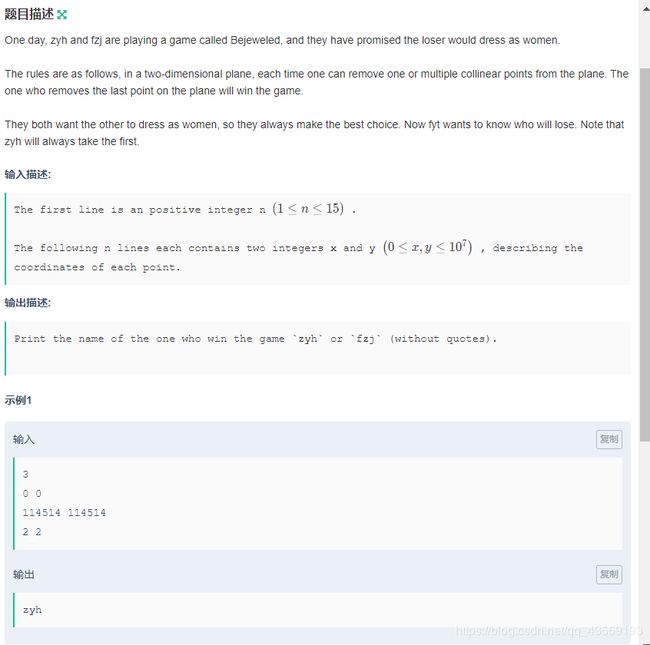
题意直接看图，
思路： 根据样例，和手写n=4,n=5,n=6的情况，可以发现规律并证明(此处不写)： 当任意三点共线，先手必胜，否则则根据点的数量来判断，如果是3的倍数，先手必败，否则必胜。 （主要思考过程是先考虑任意三点不共线来切入，然后再考虑三点的情况）。

代码：

#include
using namespace std;
const int N=1e3+15;
typedef long long ll;
ll x[N],y[N];
int main()
{
    ll n;
    cin>>n;
    for(int i=1;i<=n;i++)
    {
        cin>>x[i]>>y[i];
    }
    if(n<3)
    {
        cout<<"zyh"<<endl;return 0;
    }
    for(int i=1;i<=n-2;i++)
    {
        for(int j=i+1;j<=n-1;j++)
        {
            for(int k=j+1;k<=n;k++)
            {
                if( (x[j]-x[i])*(y[k]-y[i]) == (x[k]-x[i])*(y[j]-y[i]))
                {
                    cout<<"zyh"<<endl;return 0;
                }
            }
        }
    }
    if(n%3!=0)
    {
        cout<<"zyh"<<endl;return 0;
    }
    else
        cout<<"fzj"<<endl;
    return 0;
}