算法分析与设计--动态规划
矩阵链乘
矩阵链乘积是给定一序列矩阵,期望求出相乘这些矩阵的最有效方法。此问题并不是真的去执行其乘法,而只是决定执行乘法的顺序而已。
因为矩阵乘法具有结合律,所有其运算顺序有很多种选择。换句话说,不论如何括号其乘积,最后结果都会是一样的。下列简略证明一下为什么矩阵链乘是可结合的。


上面两个式子都等于

但括号其乘积的顺序是会影响到需计算乘积所需简单算术运算的数目,即其效率。
A 是10 × 30的矩阵, B 是30 × 5矩阵, and C 是5 × 60 矩阵
( A B ) C = ( 10 × 30 × 5 ) + ( 10 × 5 × 60 ) = 1500 + 3000 = 4500 (AB)C = (10×30×5) + (10×5×60) = 1500 + 3000 = 4500 (AB)C=(10×30×5)+(10×5×60)=1500+3000=4500
A ( B C ) = ( 30 × 5 × 60 ) + ( 10 × 30 × 60 ) = 9000 + 18000 = 27000 A(BC) = (30×5×60) + (10×30×60) = 9000 + 18000 = 27000 A(BC)=(30×5×60)+(10×30×60)=9000+18000=27000
明显地,第一种方式要有效多了。既然已确认过此问题了,那要如何决定n个矩阵相乘的最佳顺序呢?
我们通过一个数组 p[]用于保存每个矩阵的行和列。比如上面三个矩阵我们需要一个长度为4的数组,
p[0]=10
p[1]=30
p[2]=5
p[3]=60
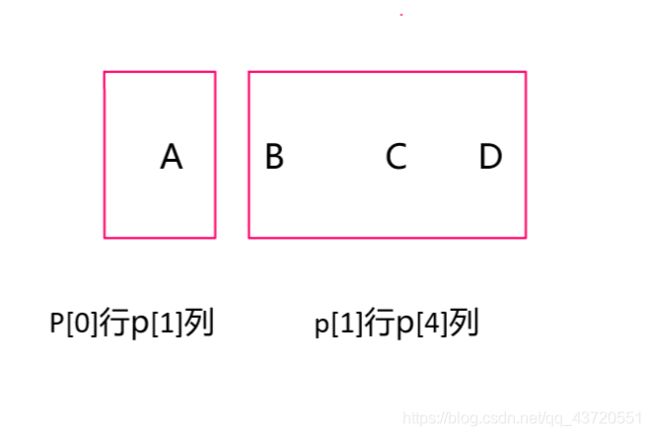
假设将矩阵已经链乘到剩下最后两个矩阵,那么这两个矩阵乘起来的操作数是:op(A)+op(BCD)+p[0]*p[1]*p[4]
递归出口是只操作一个矩阵。
public static int matrixChainOrder(int i,int j,int[] p)
{
//第i个矩阵到第j个矩阵之间最少的链乘操作数。
if(i==j)
return 0;
int min=Integer.MAX_VALUE;
for(int k=i;k<j;k++)
{
//要有一个k,用于分割
int cur_min=matrixChainOrder(i,k,p)+matrixChainOrder(k+1, j, p)+p[i-1]*p[k]*p[j];
if(cur_min<min)
min=cur_min;
}
return min;
}
public static int matrixChainOrder(int[] p) {
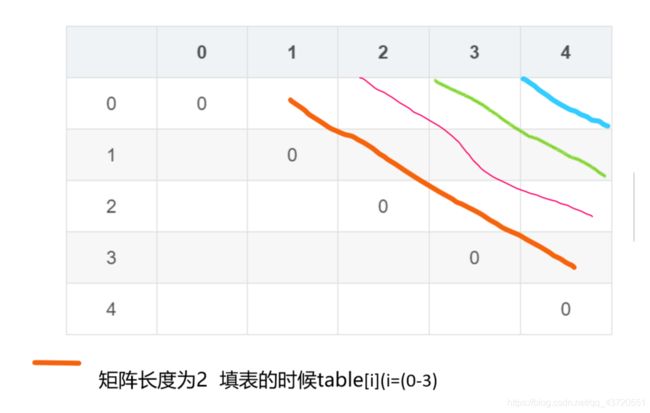
int[][] table = new int[p.length][p.length];
for (int i = 1; i < table.length; i++)
table[i][i] = 0;
//l是链的长度。
for (int l = 2; l < table.length; l++) {
for (int i = 1; i < table.length - l + 1; i++) {
int j = i + l - 1;
table[i][j] = Integer.MAX_VALUE;
for (int k = i; k < j; k++) {
int cost = table[i][k] + table[k + 1][j] + p[i - 1] * p[k] * p[j];
if (cost < table[i][j])
table[i][j] = cost;
}
}
}
return table[1][p.length - 1];
}
合并石子堆
石子堆合并问题
n堆石子堆,每堆石子个数可能不一样,用数组来保存每堆石子的个数,只能合并两堆相邻的石子。每合并一次,就有一个工作量,工作量是合并两个石子堆的石子数之和。
经过n-1次合并成一个,求最少工作量。
这道题和上述矩阵链乘十分相似。
- 递归解法
public static int minWork1(int[] arr, int i, int j) {
// 合并石子堆,递归算法
if (i == j)
return 0;
int cur_min = Integer.MAX_VALUE;
for (int k = i; k < j; k++) {
int a = minWork1(arr, i, k) + minWork1(arr, k + 1, j) + work(arr, i, j);
if (a < cur_min)
cur_min = a;
}
return cur_min;
}
public static int work(int[] arr, int i, int j) {
int sum = 0;
for (int k = i; k <= j; k++) {
sum = sum + arr[k];
}
return sum;
}
2.动态规划
public static int work(int[] arr, int i, int j) {
int sum = 0;
for (int k = i; k <= j; k++) {
sum = sum + arr[k];
}
return sum;
}
public static int minWork2(int[] arr) {
//动态规划
int[][] table = new int[arr.length][arr.length];
for (int i = 0; i < table.length; i++)
table[i][i] = 0;
for (int l = 2; l <= table.length; l++) {
for (int i = 0; i < table.length - l + 1; i++) {
int j = i + l - 1;
int min = Integer.MAX_VALUE;
for (int k = i; k < j; k++) {
int a = table[i][k] + table[k + 1][j] + work(arr, i, j);
if (a < min)
min = a;
}
table[i][j] = min;
}
}
return table[0][table.length - 1];
}
- 利用链表
public static int minWork(ArrayList<Integer> stone) {
int sum = 0;
while (stone.size() > 1) {
int min = stone.get(0) + stone.get(1);
int s = 0;
for (int i = 1; i < stone.size() - 1; i++) {
//找到最小的相邻的两个石子堆之和,并且用s跟踪
int a = stone.get(i) + stone.get(i + 1);
if (a < min) {
min = a;
s = i;
}
}
//将两个石子堆删除,添加两个石子堆之和
stone.remove(s);
stone.remove(s);
stone.add(s, min);
sum = sum + min;
}
return sum;
}
最长公共子序列
给定两个序列,找出两个序列中存在的最长子序列的长度。子序列是以相同的相对顺序出现,但不一定是连续的序列。例如,“ abc”,“ abg”,“ bdf”,“ aeg”,“ acefg”等是“ abcdefg”的子序列。
思路:
X1 X2 X3 X4……Xn
X1 X2 X3 X4……Xm
我们假设 两个字符串的最长公共子序列长度为 lcs(s1[1……n],s2[1……m])
(1)如果x1=x1,则继续求后面两个的子字符串的公共子序列长度。lcs(s1[1……n],s2[1……m])=1+lcs(s1[2……n],s2[2……m])
(2)如果x1≠x1。
lcs(s1[1……n],s2[1……m])=max(lcs(s1[1……n],s2[2……m]),lcs(s1[2……n],s2[1……m]))
public static int longestCommonSubsequence(String text1,String text2)
{
if(text1.length()==0||text1.length()==0)
return 0;
if(text1.charAt(0)==text2.charAt(0))
return 1+longestCommonSubsequence(text1.substring(1), text2.substring(1));
else
return Math.max(longestCommonSubsequence(text1, text2.substring(1)), longestCommonSubsequence(text1.substring(1), text2));
}
子序列的问题很多是可以通过动态规划来解决的。此时我们需要一个表格,动态规划就是通过空间换取时间,所以很多动态规划都可以通过建立表格来求解。
例如
s1=“abefd”
s2=“aeg”
| “” | a | b | e | f | g | |
|---|---|---|---|---|---|---|
| “” | 0 | 0 | 0 | 0 | 0 | 0 |
| a | 0 | |||||
| e | 0 | |||||
| g | 0 | 答案 |
空串和任何字符串都没有公共子序列,所以长度为0;
如果 s 2 [ i ] = = s 1 [ j ] s2[i]==s1[j] s2[i]==s1[j]
t a b l e [ i ] [ j ] = 1 + t a b l e [ i − 1 ] [ j − 1 ] table[i][j]=1+table[i-1][j-1] table[i][j]=1+table[i−1][j−1]
否则
t a b l e [ i ] [ j ] = m a x ( t a b l e [ i ] [ j − 1 ] , t a b l e [ i − 1 ] [ j ] ) table[i][j]=max(table[i][j-1],table[i-1][j]) table[i][j]=max(table[i][j−1],table[i−1][j])
用表格还有另一个好处,就是填写表格十分容易。