在前面复习了三个简单排序Java数据结构和算法(三)--三大排序--冒泡、选择、插入排序,属于算法的基础,但是效率是偏低的,所以现在学习高级排序
插入排序存在的问题:
插入排序在逻辑把数据分为两部分,左边:数据是有序的,右边:数据是无序的
上图中的元素2,是最小的数据,但是在最右边,我们需要和之前的元素进行比较,然后每个元素都要后移,直到找到应该插入的位置,这里
对于元素2来说,所有的元素都要后移一位
这个过程将近存在N次复制,移位的次数平均N/2,所以执行效率是O(N^2)
所以如果能以某种方式不需要一个个移动所有的中间项,就能把较小的数据项移动到左边,那么执行效率会很大的改进
希尔排序:
希尔排序因为计算机科学家Donald L. Shell而闻名,在插入排序的基础上,增加了一个特性,大大提高插入排序的执行效率
通过加大插入排序元素之间的间隔,且在这些有间隔的元素中进行插入排序,从而使数据项大幅度的移动。这样经过一轮排序后,然后减小
数据项的间隔再进行排序,依次进行。进行排序时数据项之间的间隔被称为增量,习惯上用h表示
在完成上面的一轮排序之后,数组中的元素已经"基本有序",我们知道插入排序对于"基本有序"的数组排序效率是很高的
如果每次插入只需要移动一到两次,算法的效率是O(N)
减小间隔:
对于更大的数组来说,刚开始的间隔应该更大,再逐渐缩小,直到间隔变成1
一般采用2.2来整除得到增量间隔,例如100,间隔分别是45,20,9,4,1,事实证明了这样比用2会整除会显著的改善排序效果
还有一种很常用的间隔序列:knuth 间隔序列 3h+1
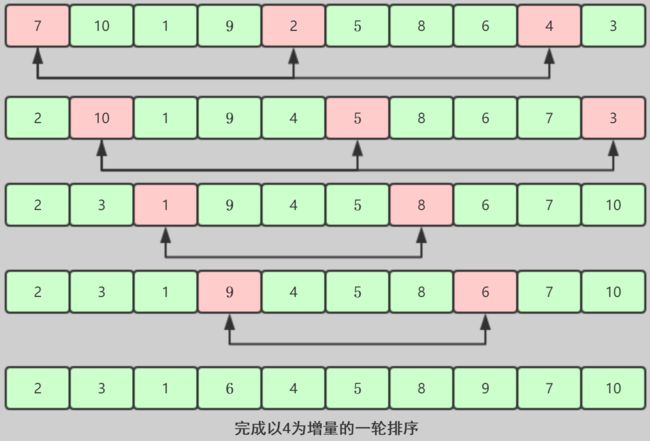
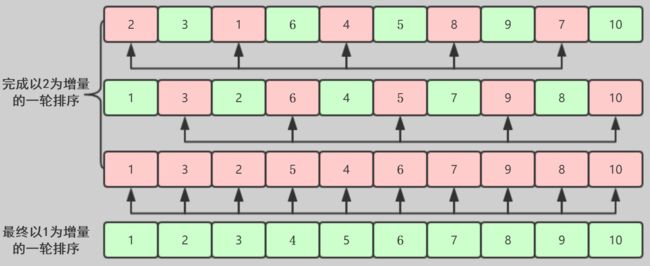
图例:
就这样可以完成排序
代码示例:
public class ShellSort {
private long[] elementArray;
private int nItems;
public ShellSort(int max) {
elementArray = new long[max];
nItems = 0;
}
public void insert(long value) {
elementArray[nItems++] = value;
}
public void display() {
for (int i = 0; i < nItems; i++) {
System.out.print(elementArray[i] + " ");
}
System.out.println("");
}
public void sort() { //基于knuth容量间隔的希尔排序
int i, j;
long temp;
int h = 1;
while (h <= nItems/3) //确定容量间隔
h = h*3+1;
while (h > 0) { //保证缩小间隔最终为1
for (i = h; i < nItems; i++) {
temp = elementArray[i];
j = i;
while (j > h-1 && temp < elementArray[j-h]) { //这里就是插入排序的逻辑了,每个间隔分组进行排序
elementArray[j] = elementArray[j-h];
j -= h;
}
elementArray[j] = temp;
}
h = (h-1) / 3;
}
}
}
public static void main(String[] args) {
ShellSort shellSort = new ShellSort(10);
shellSort.insert(7);
shellSort.insert(10);
shellSort.insert(1);
shellSort.insert(9);
shellSort.insert(2);
shellSort.insert(5);
shellSort.insert(8);
shellSort.insert(6);
shellSort.insert(4);
shellSort.insert(3);
shellSort.display();
shellSort.sort();
shellSort.display();
}输出结果:
7 10 1 9 2 5 8 6 4 3
1 2 3 4 5 6 7 8 9 10
分组间隔为2的希尔排序:
public void sort1() {
int i, j;
long temp;
int h;
for (h = nItems/2; h > 0; h /= 2) {
for (i = h; i < nItems; i++) {
temp = elementArray[i];
j = i;
while (j > h-1 && temp < elementArray[j-h]) {
elementArray[j] = elementArray[j-h];
j -= h;
}
elementArray[j] = temp;
}
}
}
相对插入排序,希尔排序稍微复杂一点,如果不能直接理解,可以参考上图,对照代码,一步步理解
希尔排序的效率:
除非在特殊情况,否则无法从理论分析希尔排序的效率,基于各种实验,时间级从O(N^(3/2))-O(N^(7/6))
下图是速度较慢的插入排序和速度较快的快速排序、希尔排序的评估值
快速排序:
毫无疑问,快速排序是最流行的排序算法。因为大多数情况下,快速排序的速度都是最快的,执行时间为O(N*logN)级
快速排序本质上是把一个数组划分为两个子数组,然后递归调用为每个子数组进行快速排序而实现的
左标记i向右移动,直到遇到比pivot大的元素停止,右标记往左移动,直到遇到比pivot小的元素的元素停止,直到i>=j
图例:
代码实现:
public class QuickSort{
public void sort(int[] arr) {
sort(arr, 0, arr.length - 1);
}
private void sort(int[] arr, int left, int right) {
if (right <= left) {
return;
}
//切分
int pivotIndex = partition(arr, left, right);
sort(arr, left, pivotIndex-1);
sort(arr, pivotIndex+1, right);
}
private int partition(int[] arr, int left, int right) {
int i = left;
int j = right+1;
int pivot = arr[left]; //pivot为基准元素,这里选择头文件
while(true){
while(i 0 && arr[--j] > pivot){} //右标记往左移动,直到遇到比pivot小的元素,或者到最左边,停止
if(i >= j){ //如果左右标记相遇时候停止,说明没有符合的元素,跳出循环
break;
}else{
swap(arr, i, j);//左右标记在相遇前停止,交换元素,然后继续移动
}
}
swap(arr, left, j);//基准元素和游标相遇时所指元素交换,为最后一次交换
return j;// 一趟排序完成, 返回基准元素位置(注意这里基准元素已经交换位置了)
}
private void swap(int[] arr, int i, int j){
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
} public static void main(String[] args) {
int []arr = new int[]{7, 10, 1, 9, 2, 5, 8, 6, 4, 3 };
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i] + " ");
}
System.out.println("");
QuickSort quickSort = new QuickSort();
quickSort.sort(arr);
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i] + " ");
}
}输出结果:
7 10 1 9 2 5 8 6 4 3
1 2 3 4 5 6 7 8 9 10
个人感觉快速排序思想很好理解,但是有的代码实现方式,看的真的很头疼,以下代码来自:公众号< >,相对于上面代码,不利于理解
public class QuickSort{
public static void sort(int[] arr) {
sort(arr, 0, arr.length - 1);
}
private static void sort(int[] arr, int startIndex, int endIndex) {
if (endIndex <= startIndex) {
return;
}
//切分
int pivotIndex = partition(arr, startIndex, endIndex);
sort(arr, startIndex, pivotIndex-1);
sort(arr, pivotIndex+1, endIndex);
}
private static int partition(int[] arr, int startIndex, int endIndex) {
int pivot = startIndex;//取基准值
int index = pivot + 1;//Mark初始化为起始下标
for(int i = index; i <= endIndex; i++){
if(arr[i] < arr[pivot]){
//小于基准值 则mark+1,并交换位置。
swap(arr, i, index);
index ++;
}
}
//基准值与mark对应元素调换位置
swap(arr, pivot, index - 1);
return index - 1;
}
private static void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
这里代码实现只是左标记从左向右移动,都没有右标记的概念,和他的图解都不一样,理解难度很大
PS:算法理解思想不难,但是手写就有难度了,特别是过了一段时间,很难完全写正确,可以隔段时间写一次,加深记忆,也可以在letcode上刷题
内容参考:
Java数据结构和算法(九)——高级排序