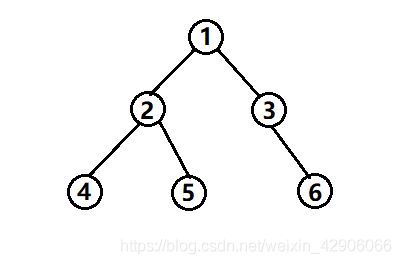
用python实现二叉树的基本操作
二叉树基本操作:
- 创建二叉树 (need)
- 递归遍历二叉树 (need)
1)前序遍历:“根-左-右”
2)中序遍历:“左-根-右”
3)后序遍历:“左-右-根” - 非递归遍历二叉树
1)前序遍历
2)中序遍历
3)后序遍历
手动创建二叉树:
方法一:
A, B, C, D, E, F = [BinaryTreeNode(x) for x in '123456']
A.left, A.right = B, C
B.left, B.right = D, E
C.right = F
方法二:
D = BinaryTreeNode(4)
E = BinaryTreeNode(5)
F = BinaryTreeNode(6)
C = BinaryTreeNode(3, right=F)
B = BinaryTreeNode(2, left=D, right=E)
root = BinaryTreeNode(1, left=B, right=C)
二叉树结点:
class BinaryTreeNode:
def __init__(self, data=None, left=None, right=None):
self.data = data
self.left = left
self.right = right
遍历结果如下:
1)前序遍历:1、2、4、5、3、6
2)中序遍历:4、2、5、1、3、6
3)后序遍历:4、5、2、6、3、1
完整代码,如下:
# !usr/bin/env python
# -*- coding:utf-8 -*-
"""
二叉树的基本操作
@author: YAOTIANLONG
@file: DS_tree.py
@time: 2019/10/28
"""
class BinaryTreeNode:
"""二叉树结点"""
def __init__(self, data=None, left=None, right=None):
self.data = data
self.left = left
self.right = right
class BinaryTree:
"""
二叉树基本操作:
- 创建二叉树
- 判断二叉树是否为空
- 二叉树递归遍历:前序、中序、后序
- 二叉树非递归遍历:前序、中序、后序
"""
def __init__(self, root=None):
self.root = root
def is_empty(self):
return True if self.root == None else False
def preOrder(self, BinaryTreeNode):
"""递归
前序遍历
:param BinaryTreeNode:
:return:
"""
if BinaryTreeNode == None:
return
print(BinaryTreeNode.data, end=" ")
self.preOrder(BinaryTreeNode.left)
self.preOrder(BinaryTreeNode.right)
def inOrder(self,BinaryTreeNode):
"""递归
中序遍历
:param BinaryTreeNode:
:return:
"""
if not BinaryTreeNode:
return
self.inOrder(BinaryTreeNode.left)
print(BinaryTreeNode.data, end=" ")
self.inOrder(BinaryTreeNode.right)
def postOrder(self,BinaryTreeNode):
"""递归
后序遍历
:param BinaryTreeNode:
:return:
"""
if not BinaryTreeNode:
return
self.postOrder(BinaryTreeNode.left)
self.postOrder(BinaryTreeNode.right)
print(BinaryTreeNode.data, end=" ")
# 非递归遍历,参考博客https://blog.csdn.net/z_ryan/article/details/80854233
def preOrder1(self):
"""
非递归前序遍历:
当p非空或stack非空时,输出p.data并将p压入stack,遍历左子树(边遍历边打印,并把根节点存入栈中)
当无左子树时,弹出stack,遍历该节点的右子树
:param self:
:return:
"""
if self.root == None:
return
stack = []
p = self.root
while p != None or stack:
while p != None: # 边遍历边打印,并存入栈中,以后需要借助这些根节点进入右子树
print(p.data, end=' ')
stack.append(p)
p = p.left
if stack: # 当p为空时,说明根和左子树都遍历完了,该进入右子树了
p = stack.pop().right
def inOrder1(self):
"""
非递归中序遍历:
先将p和左子树压入stack,当p为空时,弹出stack并输出数据,转而将p变为右子树
:return:
"""
if self.root == None: # 空树
return
stack = []
p = self.root
while p != None or stack:
while p != None: # 一直遍历到左子树最下边,边遍历边保存根节点到栈中
stack.append(p)
p = p.left
if stack: # 当p为空时,说明已经到达左子树最下边,这时需要出栈了
s = stack.pop()
print(s.data, end=' ')
p = s.right # 进入右子树,开始新的一轮左子树遍历(这是递归的自我实现)
def postOrder1(self):
"""
非递归后序遍历
只有当左子树和右子树都被访问了,才能访问根节点
当当前根节点右子树和per相等时,说明已经可以访问该根节点了
# https://blog.csdn.net/qq_33951180/article/details/52687692
:return:
"""
if self.root == None:
return
stack = []
p,per = self.root,None
while p != None or stack:
while p != None:
stack.append(p)
p = p.left
top = stack[-1] # 栈顶元素,p指针回退
if top.right == None or top.right == per:
# top存的是当前的根节点,当top的右子树为空或者top的右子树为pos,说明右子树已经遍历过,
# 这时就可以访问当前的根节点了
print(top.data,end=' ')
per = top
stack.pop()
else:
p = top.right
if __name__ == "__main__":
#先创建叶节点
# root, B, C, D, E, F = [BinaryTreeNode(x) for x in '123456']
# root.left, root.right = B, C
# B.left, B.right = D, E
# C.right = F
D = BinaryTreeNode(4)
E = BinaryTreeNode(5)
F = BinaryTreeNode(6)
C = BinaryTreeNode(3, right=F)
B = BinaryTreeNode(2, left=D, right=E)
root = BinaryTreeNode(1, left=B, right=C)
# 遍历
bt = BinaryTree(root)
print('前序:')
bt.preOrder(bt.root)
print()
bt.preOrder1()
print()
print('中序:')
bt.inOrder(bt.root)
print()
bt.inOrder1()
print()
print('后序:')
bt.postOrder(bt.root)
print()
bt.postOrder1()
输出结果:
C:\Software\Anaconda3\envs\tf_gpu\python.exe D:/PycharmProjects/剑指offer/DS_tree.py
前序:
1 2 4 5 3 6
1 2 4 5 3 6
中序:
4 2 5 1 3 6
4 2 5 1 3 6
后序:
4 5 2 6 3 1
4 5 2 6 3 1
Process finished with exit code 0