自平衡二叉查找树 Red-Black Tree

“自平衡”

对于一棵普通的二叉搜索树，当我们逐个插入满足递减或递增性质的数据时，其树的性质就会被破坏。例如依次插入10、9、8、7、6、5，最终形成一棵以10位根的链。如果此时插入的数据很多时，就完全体现不出树状结构lgn查询的优势。在红黑树中，为了维护二叉树的树状结构，每一个结点设置成黑色或红色，在性质遭到破坏时，按照规则，对结点进行旋转或修改颜色。


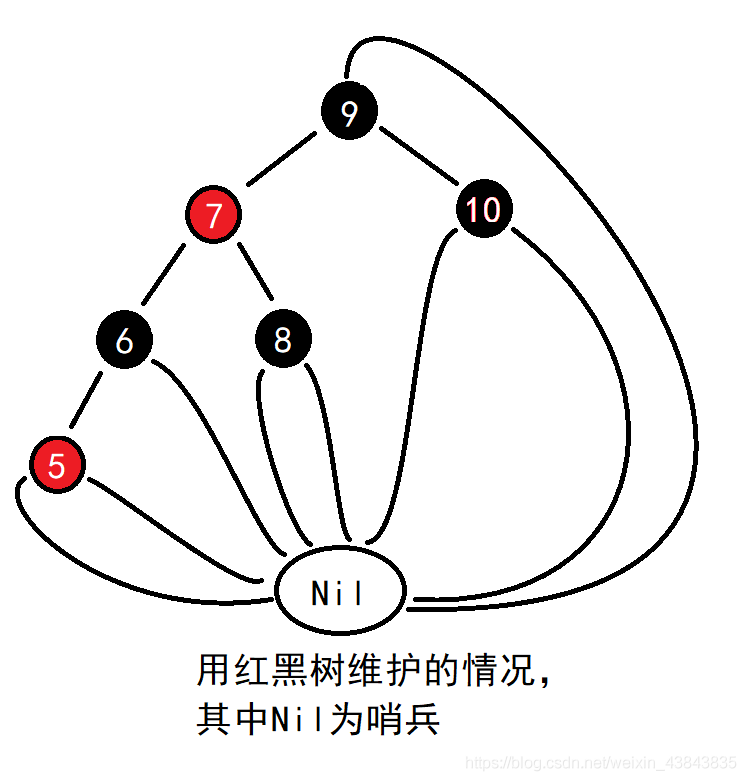
由图，利用红黑树查找值的复杂度可以是稳定的O(lgn).

红黑树的性质

通过自平衡手段，红黑树确保没有一条路径会比其它路径长出两倍以上。
为了达到平衡效果，红黑树需要满足以下五条性质：
1.每个结点或是黑色，或是红色；
2.根节点必须是黑色；
3.每个叶节点(Nil)都是黑色;
4.红色结点的两个子结点都是黑色的；
5.每条从根节点到达叶节点的简单路径经过相同数目的黑色结点。
对于每一个结点，我们设置五个属性：color，key，left，right，p。
color：结点的颜色，红或者黑；
key：结点的数值，用于结点之间的比较；
left：结点的左孩子；
right：结点的右孩子；
p：结点的父亲。
后三个属性用指针表示。
所有叶节点用一个颜色为黑色，指向根节点，值为空的Nil表示。

根据红黑树的性质，一棵包含n个结点的红黑树高度最多为2lg(n+1)。
简要推理：定义黑高bh为一条从根到叶的简单路径上经过的黑色结点数。根据性质4，最坏情况下，红色结点和黑色结点间隔出现，一棵红黑树最多包含2^2*bh-1个结点，其中一半为黑色结点。设此时有n个结点，那么bh=2lg(n+1)，也即最坏从根节点开始查找一个值需要2lg(n+1)的时间。

对红黑树的动态操作

红黑树支持插入、删除、查找值、计算最值等多种操作，且时间复杂度都为树的高度O(h),也即O(lgn)。本文重点阐述红黑树的旋转、插入和删除，查询操作视具体情况而定，不做说明。

旋转(Rotate)

由于插入和删除很可能破坏红黑树的五条性质中的其中几条，因此需要对树进行“旋转”和修改结点颜色来维护。旋转分为两种：左旋、右旋，其过程都只是修改指针指向。
假设现有一个结点x进行左旋，它的右儿子为y，旋转的目的是让y取代x的位置，x成为y的左儿子并继承y原来的左儿子。
而右旋则与左旋的过程相逆，y成为x的右儿子，且x原来的右儿子成为y的左儿子，x取代y的位置。

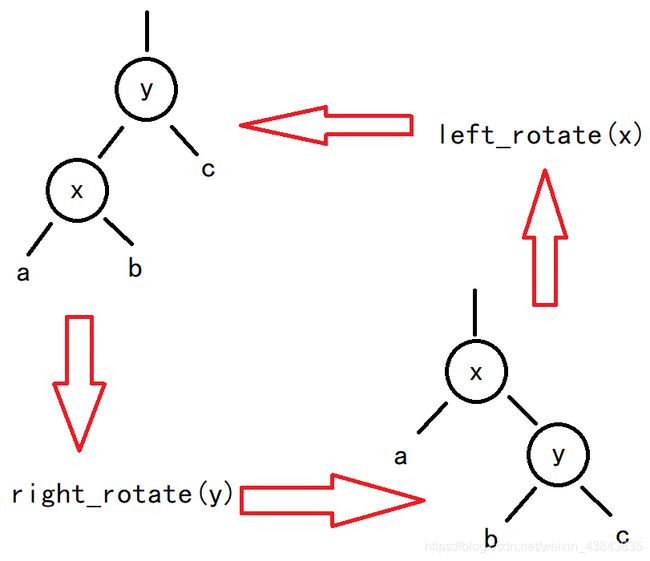
左旋伪代码：

y = x.right;			//找到x的右儿子y
x.right = y.left;		//先把y的左儿子过继给x当右儿子
if( y.left != T.nil )   
	y.left.p = x;		//如果过继过去的儿子不是叶，那就让这个儿子认x做爹
y.p = x.p;				//y的父亲设置为x的父亲
if( x.p == T.nil )		
	T.root = y;			//如果x的父亲为哨兵，则y就是根
else if( x == x.p.left )
	x.p.left = y;		
else x.p.right = y;		//判断x是他父亲的左儿子还是右儿子，并连接父亲和y
y.left = x;				//x认做y的左儿子
x.p = y;				

右旋伪代码：

x = y.left;
y.left = x.right;
if( x.right != T.nil )
	x.right.p = y;
x.p = y.p;
if( y.p == T.nil )
	T.root = x;
else if( y == y.p.left)
	y.p.left = x;
else y.p.right = x;
x.right = y;
y.p = x;

插入(Insert)

红黑树的插入与原始二叉搜索树的插入方式相同，不过在最后需要判断是否满足红黑树性质，并且更正这棵树。对于每个新加入的结点z，设置它为红色，迭代寻找z该在的位置。
(设右儿子的key大于左儿子的key）
伪代码：

y = T.nil;
x = T.root;
while ( x != T.nil )
	y = x;
	if( z.key < x.key )
		x = x.left;
	else x = x.right;
z.p = y;
if( y = T.nil )
	T.root = z;
else if ( z.key < y.key )
	y.left = z;
else y.right = z;
z.left = T.nil;
z.right = T.nil;
z.color = RED;
Insert_Fixup(T,z);

下面是最关键的调整操作
在插入一个红色结点后，它的父亲可能是红色结点，此时就需要分类调整，总共会出现三种需要调整的情况：

情况一：z的叔结点y是红色的

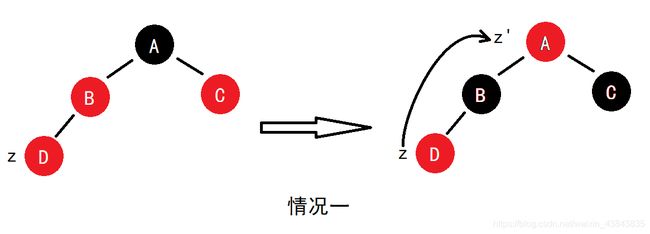
进入这种情况的前提是，B和C都为红色且A为黑色。这种情况是最好处理的，把A、B、C反色，z跳到A，往上迭代修改，直到遇到其它情况。这样的迭代只影响图中的上面三个结点，下一次迭代时可以保证z指向的结点为红色。最终，若z迭代到根结点，则意味着根结点以下的所有结点必定满足红黑树性质，所以此时只要在最后把根设置为黑色即可。

情况二：z的叔结点是黑色的，且z是右儿子
情况三：z的叔结点是黑色的，且z是左儿子

如图，情况二通过D点的左旋可以转换成情况三，我们研究情况三。情况一不断迭代有可能到达这种情况，遇到这种情况，不能只是简单地改变颜色。如图所示，需要对B的父亲A进行右旋，并修改B和A的颜色。如果这四个点以外的结点都符合红黑树的性质，则这样操作后，它们的性质保持不变，而这四个结点也符合红黑树性质。由于，每次插入的结点必定在树的底层，所以性质被破坏的部分也在树的末节处，由情况一向上迭代，整棵树最多只有这一处不符合红黑树性质，因此，情况三的出现意味着迭代结束。

伪代码：

while( z.p.color == RED )
	if( z.p == z.p.p.left)			//z位于左子树
		y = z.p.p.right;
		if ( y.color == RED ) 		//情况一
			z.p.color = BLACK;
			y.color = BLACK;
			z.p.p.color = RED;
			z = z.p.p;
		else 						//情况二、三
			if ( z == z.p.right )	//情况二转换成情况三
				Left_Rotate(T,z);
			z.p.color = BLACK;
			z.p.p.color = RED;
			Right_Rotate(T.z.p.p);
	else							//z位于右子树
		y = z.p.p.left;
		if( y.color = RED )		
			z.p.color = BLACK;
			y.color = BALCK;
			z.p.p.color = RED;
			z = z.p.p'
		else
			if( z == z.p.left )		//注意旋转方向变化
				Right_Rotate(T,z);
			z.p.color = BLACK;
			z.p.p.color = RED;
			Left_Rotate(T,z.p.p);
T.root.color = BLACK;				//纠正根结点颜色

删除(Delete)

红黑树的删除操作套用原始二叉搜索树的删除操作，同理，需要一个特别的Fixup调整红黑树。
伪代码：

Transplant(T,u,v）{
	if( u.p == T.nil )
		T.root = v;
	else if( u == u.p.left )
		u.p.left = v;
	else u.p.right = v;
	v.p = u.p;
}
Delete(T,z){
	y = z;
	y_originnal_color = y.color;
	if( z.left == T.nil )
		x = z.right;
		Transplant(T,z,z.right);
	else if ( z.right == T.nil)
		x = z.left;
		Transplant(T,z,z.left);
	else y = Mininum( z.right );		//z右子树中的最小值
		y_original_color = y.color;
		x = y.right;
		if ( y.p == z )
			x.p = y;
		else Transplant(T,y,y.right);
			y.right = z.right;
			y.right.p = y;
		Transplant(T,z,y);
		y.left = z.left;
		y.left.p = y;
		y.color = z.color;
	if( y_original_color == BLACK )
		Delete_Fixup(T,x);				//x指向被删除结点现在位置上的结点
}

首先我们需要编写一段子函数用来完成子树的移植，然后再实现删除结点z。在删除操作中分成三种情况：z的左儿子是哨兵、z的右儿子是哨兵、z有两棵子树。前两种情况比较简单，直接移植即可，顺便记录需要用于后续维护的x结点。第三种情况中，我们需要找到z右子树中最小值结点y，使其取代z成为新的“中位值”。

对于可能产生的问题进行归纳：

1.在前两种情况中，y充当被删除的结点，如果它的颜色为黑色，则删去它很可能导致两个红色结点连接；第三种情况中，y充当插入结点，如果为黑色，则可能导致y结点的原位置出现两个红色结点连接。

2.如果y是原来的根节点，并且有一个红色儿子，则根可能变成红色。

3.移走y，会导致包含y的路径失去一个黑高。如果此时把取代y的x视为黑色，则可以解决这一问题，但是这么一来，x的颜色就变得不确定的，它可能是双重黑色或者红黑色。

为了解决x颜色不确定的问题，需要把y留下的额外黑色往树的上面移动。当x指向红黑色结点时，可以把x置为黑色，处理完毕，同时解决问题1和问题2；当x指向根结点时，则可无视额外黑色，因为从下往上迭代寻找位置时，下面的黑高不平衡问题已经解决了，移向根结点时，相当于所有通向叶子的简单路径加1黑高，可以直接去除；但x指向双重黑色的，并且不是根的结点时，我们需要分4种情况讨论。

情况一：x的兄弟为红色

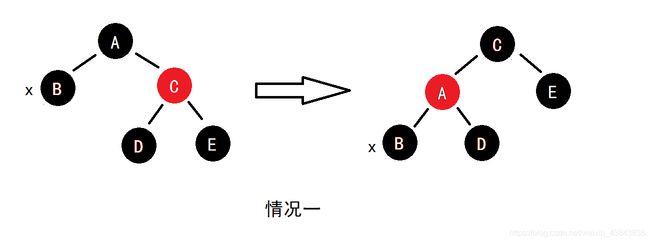
在这种情况下，对x的兄弟结点A进行一次左旋，使x的兄弟结点变成黑色。红色结点的两个儿子必为黑色，左旋不会破坏当前红黑树的性质，因此可以巧妙的把情况一转换成下面三种情况中的一种。

情况二：x的兄弟为黑色，且兄弟两个儿子都是黑色。

只有红色结点的两个儿子都是黑色结点，为了保证有空间处理这个额外的黑色，需要把一个已有的黑色结点置成红色，而把C改成红色正好不会破坏红黑树性质，此时让x指向一个红黑色结点，在下一轮循环中，变成黑色即可。

情况三：x的兄弟为黑色，且兄弟的左儿子为红色，右儿子为黑色

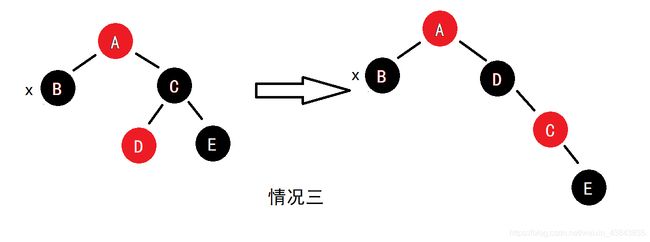
右旋C，把情况三转换成情况四。

情况四：x的兄弟为黑色，且兄弟的右儿子是红色

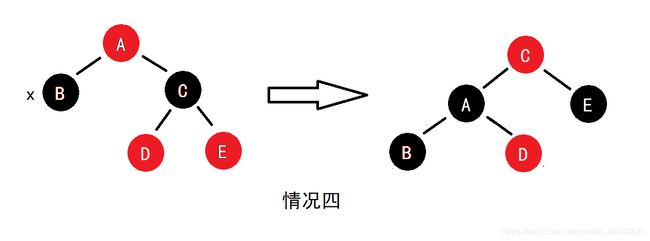
这种情况下，对A进行左旋，并改成红色，A改成黑色，从而不破坏原红黑树性质。同时把E改成黑色，确保右子树黑高不变，并且去掉额外的黑色。解决完额外黑色问题后，红黑树维护完毕，退出循环。

伪代码：

while( x != T.root && x.color == BLACK )
	if( x == x.p.left )											//x为左儿子
		w = x.p.right;
		if( w.color == RED )									//情况一
			w.color = BLACK;
			x.p.color = RED;
			Left_Rotate(T,x.p);
			w = x.p.right;
		if( w.left.color == BLACK && w.right.color == BLACK )	//情况二
			w.color = RED;
			x = x.p;
		else 								
			if( w.right.color == BALCK )						//情况三
				w.left.color = BLACK;
				w.color = RED;
				Right_Rotate(T,w);
				w = x.p.right;
			w.color = x.p.color;								//情况四
			x.p.color = BLACK;
			w.right.color = BLACK;
			Left_Rotate(T,x.p);
			x = T.root;
	else														//x为右儿子
		w = x.p.left;
		if( w.color == RED )
			w.color = BLACK;
			x.p.color = RED;
			Right_Rotate(T,x.p);
			w = x.p.left;
		if( w.left.color == BLACK && w.right.color == BLACK )
			w.color = RED;
			x = x.p;
		else
			if( w.right.color == BLACK )
				w.left.color = BLACK;
				w.color = RED;
				Right_Rotate(T,w);
				w = x.p.left;
			w.color = x.p.color;
			x.p.color = BLACK:
			w.right.color = BLACK;
			Right_Rotate(T,x.p);
			x = T.root;
x.color = BLACK;