牛客小白月赛25【A - J】
题目链接:https://ac.nowcoder.com/acm/contest/5600
沉寂了快三个月了,3个月来的第一篇博客~ (Minecraft mod 还没做好,如果后面有机会的话,我可以更新mod开发教程,扯偏了 )
这场的话,手感不好,疯狂罚时,而且写的也很慢,最后才7题…后来发现卡我的那题居然是没有push,还有一题被卡精度,过题人最少的那题我看都没看,就是个排列组合而已,可惜…
牛客小白月赛A-J题解
- A - AOE还是单体?
- B - k-size字符串
- C - 白魔法师
- D - 抽卡
- E - 点击消除
- F - 疯狂的自我检索者
- G - 解方程
- H - 神奇的字母(二)
- I - 十字爆破
- J - 异或和之和
我的程序头(节省篇幅)
#includeA - AOE还是单体?
当剩下的怪的数量大于等于x的时候,显然用第二个技能是不亏甚至是赚的。
那就从一开始疯狂用二技能,当只剩下x-1只怪时,再用第一技能呗~
int n,m;
char str[N];
int f[N];
int main()
{
rr(n,m);
FOR(i,1,n) r(f[i]);
sort(f+1,f+n+1);
LL ans=0;
if(m>n){
FOR(i,1,n){
ans+=f[i];
}
cout<<ans<<endl;
return 0;
}
for(int i=n;i>=n-m+2;i--){
ans+=f[i];
}
ans-=1ll*(m-1)*f[n-m+1];
ans+=1ll*f[n-m+1]*m;
cout<<ans<<endl;
return 0;
}
B - k-size字符串
这题就是我没看的那题,有点可惜…
这样想,k最小是2(此时a一边,b一边)k最大是多少?
(ababab这样拍显然利用率最高,但n和m肯定不会都那么接近)
不难发现,和 min(a,b) 有关 LL maxx=tmp+min(max(a,b),tmp+1);
然后,肯定是a b各贡献一半段,如果k为奇数那就a或b多贡献一段
怎么算这个贡献呢?(我用的是高中学的隔板法)
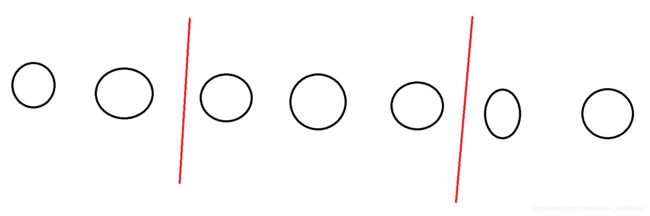
假如说有7个相同的球,我们想分为3段,那就插3-1个板子进去,可以放的位置有7-1个(根据排列组合得: C 6 2 C_{6}^{2} C62 ) 以此类推即可
LL qpow(LL a,LL p)
{
LL res=1;
while(p){
if(p&1) res=res*a%mod;
a=a*a%mod;
p>>=1;
}
return res;
}
LL inv(LL x)
{
return qpow(x,mod-2);
}
LL hhh(LL n,LL m)
{
LL res=1;
FOR(i,1,m){
res=res*(n-i+1)%mod;
res=res*inv(i)%mod;
}
return res;
}
int main()
{
LL a,b,c;
rrr(a,b,c);
LL tmp=min(a,b);
LL maxx=tmp+min(max(a,b),tmp+1);
LL ans=0;
if(c>=2&&c<=maxx){
tmp=c/2;
if(c&1){
if(b>tmp){
ans=(ans+hhh(a-1,tmp-1)*hhh(b-1,tmp)%mod)%mod;
}
if(a>tmp){
ans=(ans+hhh(a-1,tmp)*hhh(b-1,tmp-1)%mod)%mod;
}
}
else{
ans=hhh(a-1,tmp-1)*hhh(b-1,tmp-1)%mod*2%mod;
}
}
cout<<ans<<endl;
return 0;
}
C - 白魔法师
这题不知道我是不是搞复杂了( bfs+并查集 )
最后因为bfs时没有push,疯狂WA
思路都是,把一开始白连通块的作为一个集合,黑的不管。
然后找所有的黑的,假如把它变白了,那和它相连的白连通块就能合并起来 因为一开始记录了,所以查询O(1)解决
int n,m;
char str[N];
int f[N];
int dad[N];
vector<int> v[N];
bool vis[N];
int seek(int k)
{
return dad[k]==k?k:dad[k]=seek(dad[k]);
}
void bfs(int x)
{
queue<int> q;
q.push(x);
vis[x]=1;
int ans=1;
while(q.size()){
int now=q.front();
q.pop();
for(int y:v[now]){
if(!vis[y]&&str[y]=='W'){
vis[y]=1;
q.push(y);
ans++;
int xx=seek(x);
int yy=seek(y);
if(xx!=yy){
dad[xx]=yy;
}
}
}
}
f[seek(x)]=ans;
}
int main()
{
r(n);
sss(str);
FOR(i,1,n-1){
int a,b;
rr(a,b);
v[a].pb(b);
v[b].pb(a);
}
FOR(i,1,n) dad[i]=i;
FOR(i,1,n){
if(str[i]=='W'&&!vis[i]){
bfs(i);
}
}
int ans=0;
FOR(i,1,n){
ans=max(ans,f[seek(i)]);
// cout<
}
FOR(i,1,n){
if(str[i]=='B'){
int res=1;
for(int x:v[i]){
if(str[x]=='W'){
res+=f[dad[x]];
}
}
ans=max(ans,res);
}
}
cout<<ans<<endl;
return 0;
}
D - 抽卡
这题逆向思维,求出得不到的概率,然后用1减就ok
用到了逆元
int n,m;
char str[N];
int f[N],g[N];
LL qpow(LL a,LL p)
{
LL res=1;
while(p){
if(p&1) res=res*a%mod;
a=a*a%mod;
p>>=1;
}
return res;
}
LL inv(LL a)
{
return qpow(a,mod-2);
}
int main()
{
r(n);
FOR(i,1,n){
r(f[i]);
}
FOR(i,1,n){
r(g[i]);
}
LL ans=1;
LL a=1,b=1;
FOR(i,1,n){
a=a*(f[i]-g[i])%mod;
b=b*f[i]%mod;
ans=ans*inv(f[i])%mod;
}
cout<<(b-a+mod)%mod*ans%mod<<endl;
return 0;
}
E - 点击消除
和括号匹配差不多
int n,m;
char str[N];
char ans[N];
int f[N];
int main()
{
sss(str);
n=strlen(str+1);
stack<char> s;
m=0;
FOR(i,1,n){
if(m>0){
if(ans[m]==str[i]){
--m;
continue;
}
}
ans[++m]=str[i];
}
if(m==0) cout<<0;
FOR(i,1,m) cout<<ans[i];
cout<<endl;
return 0;
}
F - 疯狂的自我检索者
最大的可能就是不知道的全部投5分,最小的就是不知道的全部投1分
int n,m;
char str[N];
int f[N];
int main()
{
rr(n,m);
LL sum=0;
FOR(i,1,n-m){
r(f[i]);
sum+=f[i];
}
double ans1=(sum+5*m)*1.0/n;
double ans2=(sum+m)*1.0/n;
printf("%.5f %.5f\n",ans2,ans1);
return 0;
}
G - 解方程
一开始就开的这题,没想到被卡精度了
我甚至一度怀疑自己二分写错了(最后就判断循环了2000次就跳出即可)
int n,m;
char str[N];
LL f[N];
int main()
{
int a,b,c;
rrr(a,b,c);
double l=0,r=1e9;
int cnt=0;
while(r-l>=eps){
cnt++;
if(cnt>=2000) break;
double mid=(l+r)/2;
// cout<
double sum=1;
FOR(i,1,a){
sum*=mid;
}
sum+=b*log(mid);
if(sum>=c){
r=mid-eps;
}
else{
l=mid+eps;
}
}
printf("%.7f\n",l);
return 0;
}
H - 神奇的字母(二)
这题输入方式有点奇葩
int n,m;
char str[N];
int f[N];
int main()
{
while(~scanf("%s",str+1)){
int len=strlen(str+1);
for(int i=1;i<=len;i++){
// cout<<'*'<
if(str[i]>='a'&&str[i]<='z'){
f[str[i]-'a'+1]++;
}
}
}
char ans='a';
int maxx=0;
FOR(i,1,26){
if(f[i]>maxx){
maxx=f[i];
ans=(char)('a'+i-1);
}
}
cout<<ans<<endl;
return 0;
}
I - 十字爆破
我这样写的还不够简洁,其实一个数组f[N]就够了
就是个前缀和的思想(我写的还不是前缀和,我是统计)
int n,m;
char str[N];
char ans[N];
int f[N];
LL a[N],b[N];
int get(int x,int y)
{
return f[m*x+y];
}
int main()
{
rr(n,m);
FOR(i,0,n-1){
FOR(j,0,m-1){
r(f[m*i+j]);
}
}
FOR(i,0,n-1){
a[i]=0;
FOR(j,0,m-1){
a[i]+=get(i,j);
}
}
FOR(i,0,m-1){
b[i]=0;
FOR(j,0,n-1){
b[i]+=get(j,i);
}
}
FOR(i,0,n-1){
FOR(j,0,m-1){
cout<<a[i]+b[j]-get(i,j)<<' ';
}
cout<<endl;
}
return 0;
}
J - 异或和之和
按位考虑,假如现在是第i位,有x个1,y个0 (x+y=n)
那这一位有效的情况无非就是【1 0 0】或【1 1 1】 也就是 C x 1 ∗ C y 2 + C x 3 C_{x}^{1}*C_{y}^{2}+C_{x}^{3} Cx1∗Cy2+Cx3
其实好像不需要逆元,我又多此一举了
int n,m;
char str[N];
int f[M];
LL qpow(LL a,LL p)
{
LL res=1;
while(p){
if(p&1) res=res*a%mod;
a=a*a%mod;
p>>=1;
}
return res;
}
LL inv(LL a)
{
return qpow(a,mod-2);
}
int main()
{
r(n);
FOR(i,1,n){
LL a;
r(a);
FOR(i,0,62){
if((a>>i)&1){
f[i]++;
}
}
}
LL ans=0;
FOR(i,0,62){
LL x=f[i],y=n-f[i];
if(x>=1&&y>=2){ //1 0 0
ans=(ans+(1ll<<i)%mod*x%mod*y%mod*(y-1)%mod*inv(2)%mod)%mod;
}
if(x>=3){ // 1 1 1
ans=(ans+(1ll<<i)%mod*x%mod*(x-1)%mod*(x-2)%mod*inv(6)%mod)%mod;
}
}
cout<<ans<<endl;
return 0;
}
题目不难,但我太不熟练了…