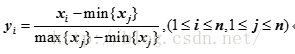数据分析与挖掘之数据预处理

目录

数据集成

简单变换

数据规范化—标准化

1、离差标准化（归一化）

2、Z-score标准化（0-1标准化）

3、小数定标规范化

数据规范化—离散化

1、等宽离散化

2、等频率离散化

3、优化离散

---

数据集成

#数据集成
import numpy
a=numpy.array([[1,5,6],[9,4,3]])
b=numpy.array([[6,36,7],[2,3,39]])
c=numpy.concatenate((a,b))  #数据整合

简单变换

1、数据变换的目的是将数据转换为更方便分析的数据

2、简单变换通常使用函数变换的方式进行，常见的函数变换包括：开方，平方，对数等；

数据规范化—标准化

数据规范化（归一化）处理是数据挖掘的一项基础工作。不同评价指标往往具有不同的量纲，数值间的差别可能很大，不进行处理可能会影响到数据分析的结果。为了消除指标之间的量纲和取值范围差异的影响，需要进行标准化处理，将数据按照比例进行缩放，使之落入一个特定的区域，便于进行综合分析。如将工资收入属性值映射到[-1, 1]或者[0, 1]内。

一、中心化（又叫零均值化）和标准化（又叫归一化）概念及目的？

1、在回归问题和一些机器学习算法中，以及训练神经网络的过程中，通常需要对原始数据进行中心化（Zero-centered或者Mean-subtraction（subtraction表示减去））处理和标准化（Standardization或Normalization）处理。

1. 意义：数据中心化和标准化在回归分析中是取消由于量纲不同、自身变异或者数值相差较大所引起的误差；对特殊模型数据标准化，能够加速权重参数的收敛。对数据进行中心化预处理，这样做的目的是要增加基向量的正交性。 原理
2. 数据标准化：是指数值减去均值，再除以标准差；
3. 数据中心化：是指变量减去它的均值。
4. 目的：通过中心化和标准化处理，得到均值为0，标准差为1的服从标准正态分布的数据。

下图中以二维数据为例：左图表示的是原始数据；中间的是中心化后的数据，数据被移动大原点周围；右图将中心化后的数据除以标准差，得到为标准化的数据，可以看出每个维度上的尺度是一致的（红色线段的长度表示尺度）。
其实，在不同的问题中，中心化和标准化有着不同的意义，

1、离差标准化（归一化）

也叫最大最小标准化，其核心思想是把原始数据的数值线性变换到[0,1]之间，公式如下：

其中，max、min分别为样本数据的最大值、最小值。

优点：保留源数据存在的关系，消除不同数据之间的量纲影响，方便数据比较和共同处理，比如在神经网络中，归一化可以加快训练网络的收敛性； 

缺点：极易受个别离群值影响，如果数据集中某个数值很大，其他各值归一化后会接近0；此外，如果遇到超出[min，max]的值，会出现错误。

2、Z-score标准化（0-1标准化）

也叫标准差标准化，这种方法给予原始数据的均值（mean）和标准差（standard deviation）进行数据的标准化。经过处理的数据符合标准正态分布，即均值为0，标准差为1。

其中μ为所有样本数据的均值，σ为所有样本数据的标准差。

优点：标准化是为了方便数据的下一步处理，而进行的数据缩放等变换，并不是为了方便与其他数据一同处理或比较，比如数据经过零-均值标准化后，更利于使用标准正态分布的性质，进行处理 ；

3、小数定标规范化

该方法是通过移动特征数据的小数位数，将其转换到[-1,1]之间，移动的小数位由特征值绝对值的最大值决定，公式如下：

K=log10（x的绝对值的最大值）

三种常用标准化的代码实现：

#导入数据
import pymysql
import numpy as npy
import pandas as pda
import matplotlib.pylab as pyl
pyl.rcParams['font.sans-serif']=['SimHei']  # 用来正常显示中文标签  
pyl.rcParams['axes.unicode_minus']=False  # 用来正常显示负号
conn=pymysql.connect(host="127.0.0.1",user="root",password="root",db="csdn")
sql="select  hits,comment from hexun"  
data=pda.read_sql(sql,conn)
#离差标准化
data2=(data-data.min())/(data.max()-data.min())
#标准差标准化
data3=(data-data.mean())/data.std()
#小数定标规范化--消除单位影响
k=npy.ceil(npy.log10(data.abs().max()))#绝对值的最大值（进1取整：1.1→2）
data4=data/10**k  

 

数据规范化—离散化

离散化，把无限空间中有限的个体映射到有限的空间中去，以此提高算法的时空效率。离散化指把连续型数据切分为若干“段”，也称bin，是数据分析中常用的手段。切分的原则有等距，等频，优化，或根据数据特点而定。在营销数据挖掘中，离散化得到普遍采用。究其原因，有这样几点： ①算法需要。例如决策树，NaiveBayes等算法本身不能直接使用连续型变量，连续型数据只有经离散处理后才能进入算法引擎。这一点在使用具体软件时可能不明显。因为大多数数据挖掘软件内已经内建了离散化处理程序，所以从使用界面看，软件可以接纳任何形式的数据。但实际上，在运算决策树或NaiveBayes模型前，软件都要在后台对数据先作预处理。 ②离散化可以有效地克服数据中隐藏的缺陷：使模型结果更加稳定。例如，数据中的极端值是影响模型效果的一个重要因素。极端值导致模型参数过高或过低，或导致模型被虚假现象“迷惑”，把原来不存在的关系作为重要模式来学习。而离散化，尤其是等距离散，可以有效地减弱极端值和异常值的影响， ③有利于对非线性关系进行诊断和描述：对连续型数据进行离散处理后，自变量和目标变量之间的关系变得清晰化。如果两者之间是非线性关系，可以重新定义离散后变量每段的取值，如采取0，1的形式， 由一个变量派生为多个哑变量，分别确定每段和目标变量间的联系。这样做，虽然减少了模型的自由度，但可以大大提高模型的灵活度。 即使在连续型自变量和目标变量之间的关系比较明确，例如可以用直线描述的情况下，对自变量进行离散处理也有若干优点。一是便于模型的解释和使用，二是可以增加模型的区别能力。常见的正态假设是连续变量，离散化减少了对于分布假设的依赖性，因此离散数据有时更有效。

1、等宽离散化

将连续型变量的取值范围均匀划成n等份，每份的间距相等。例如，客户订阅刊物的时间是一个连续型变量，可以从几天到几年。采取等距切分可以把1年以下的客户划分成一组，1-2年的客户为一组，2-3年为一组..，以此类分，组距都是一年。

2、等频率离散化

:把观察点均匀分为n等份，每份内包含的观察点数相同。还取上面的例子，设该杂志订户共有5万人，等频分段需要先把订户按订阅时间按顺序排列，排列好后可以按5000人一组，把全部订户均匀分为十段。 等距和等频在大多数情况下导致不同的结果。等距可以保持数据原有的分布，段落越多对数据原貌保持得越好。等频处理则把数据变换成均匀分布，但其各段内观察值相同这一点是等距分割作不到的。

3、优化离散

需要把自变量和目标变量联系起来考察。切分点是导致目标变量出现明显变化的折点。常用的检验指标有卡方，信息增益，基尼指数，或WOE(要求目标变量是两元变量)

#连续型数据离散化
#等宽离散化
data1=data[u"hits"].copy()  #U避免变量转换
data1=data1.fillna(data1.mean())  #缺失值均值替换
data2=data1.T  #转置
data3=data2.values  #转换成数组
k=4  #等宽4份
c1=pda.cut(data3,k,labels=["低关注","一般","适中","高价值"])
#等频率离散化
k=[0,500,1000,3000,5000,20000,data2.max()]  #等频分层
c2=pda.cut(data3,k,labels=["低关注","一般","适中","较好","非常好","异常好 "])