常见查找排序算法的Python实现及时间复杂度分析

一、顺序查找算法及分析

顺序查找（Sequential Search）：

首先从列表的第1个数据项开始，按照下标增长的顺序，逐个比对数据项，如果到最后一个都未发现要查找的项，那么查找失败

程序代码：

无序表查找代码：

def sequentialSearch(alist, item):
    pos = 0
    found = False
    
    while pos < len(alist) and not found:
        if alist[pos] == item:
            found = True
        else:
            pos = pos+1

    return found

testlist = [1, 2, 32, 8, 17, 19, 42, 13, 0]
print(sequentialSearch(testlist, 3))
print(sequentialSearch(testlist, 13))

有序表查找代码：

def orderedSequentialSearch(alist, item):
    pos = 0
    found = False
    stop = False
    while pos < len(alist) and not found and not stop:
        if alist[pos] == item:
            found = True
        else:
            if alist[pos] > item:
                stop = True
            else:
                pos = pos+1

    return found

testlist = [0, 1, 2, 8, 13, 17, 19, 32, 42,]
print(orderedSequentialSearch(testlist, 3))
print(orderedSequentialSearch(testlist, 13))

算法分析：

数据项是否在列表中，比对次数是不一样的

如果数据项不在列表中，需要比对所有数据项才能得知，比对次数是n

如果数据项在列表中，最好的情况，第1次比对就找到最坏的情况，要n次比对，所以平均状况下，比对的次数是n/2

顺序查找无序表的各种情况分析：

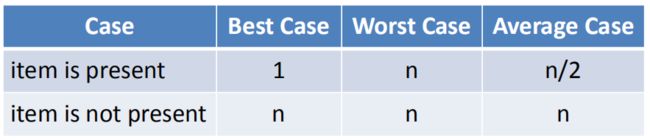
顺序查找有序表的各种情况分析：

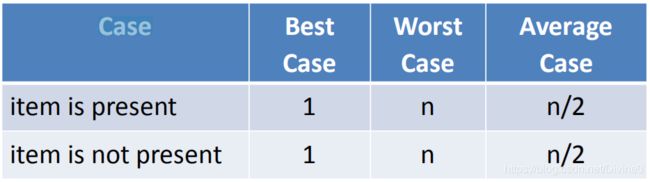
有序表的查找能节省一些比对次数，但并不改变其数量级，所以顺序查找的算法复杂度是O(n)

二、二分查找算法及分析

二分查找（Binary Search）：

针对有序表，从列表中间开始比对，如果列表中间的项匹配查找项，则查找结束，如果不匹配，那么就有两种情况：

• 列表中间项比查找项大，那么查找项只可能出现在前半部分
• 列表中间项比查找项小，那么查找项只可能出现在后半部分

无论如何，我们都会将比对范围缩小到原来的一半：n/2

继续采用上面的方法查找，每次都会将比对范围缩小一半

程序代码：

def binarySearch(alist, item):
    first = 0
    last = len(alist)-1
    found = False

    while first<=last and not found:
        midpoint = (first + last)//2
        if alist[midpoint] == item:
            found = True
        else:
            if item < alist[midpoint]:
                last = midpoint-1
            else:
                first = midpoint+1

    return found

testlist = [0, 1, 2, 8, 13, 17, 19, 32, 42,]
print(binarySearch(testlist, 3))
print(binarySearch(testlist, 13))

递归实现：

def binarySearch(alist, item):
    if len(alist) == 0:
        return False
    else:
        midpoint = len(alist)//2
        if alist[midpoint]==item:
          return True
        else:
          if item<alist[midpoint]:
            return binarySearch(alist[:midpoint],item)
          else:
            return binarySearch(alist[midpoint+1:],item)

testlist = [0, 1, 2, 8, 13, 17, 19, 32, 42,]
print(binarySearch(testlist, 3))
print(binarySearch(testlist, 13))

算法分析：

由于二分查找，每次比对都将下一步的比对范围缩小一半每次比对后剩余数据项如下表所示：

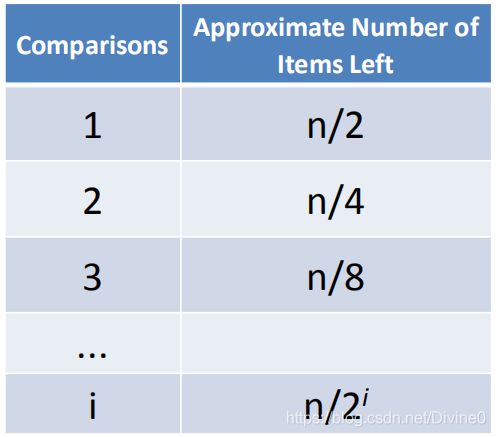
当比对次数足够多以后，比对范围内就会仅剩余1个数据项

无论这个数据项是否匹配查找项，比对最终都会结束，解下列方程：

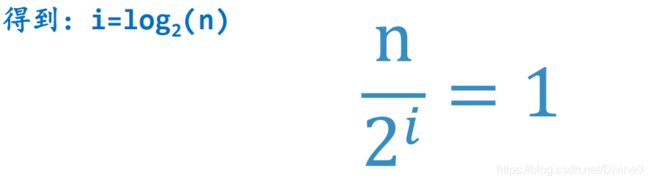
所以二分法查找的算法复杂度是O(log n)

三、冒泡排序和选择排序算法及分析

冒泡排序（Bubble Sort）：

冒泡排序的算法思路在于对无序表进行多趟比较交换， 每趟包括了多次两两相邻比较，并将逆序的数据项互换位置，最终能将本趟的最大项就位

经过n-1趟比较交换，实现整表排序每趟的过程类似于“气泡”在水中不断上浮到水面的经过

程序代码：

def bubbleSort(alist):
    for passnum in range(len(alist)-1,0,-1):
        for i in range(passnum):
            if alist[i]>alist[i+1]:
                temp = alist[i]
                alist[i] = alist[i+1]
                alist[i+1] = temp

alist = [54,26,93,17,77,31,44,55,20]
bubbleSort(alist)
print(alist)

改进冒泡排序：

def shortBubbleSort(alist):
    exchanges = True
    passnum = len(alist)-1
    while passnum > 0 and exchanges:
       exchanges = False
       for i in range(passnum):
           if alist[i]>alist[i+1]:
               exchanges = True # 通过监测每趟比对是否发生过交换，可以提前确定排序是否完成
               temp = alist[i]
               alist[i] = alist[i+1]
               alist[i+1] = temp
       passnum = passnum-1

alist=[20,30,40,90,50,60,70,80,100,110]
shortBubbleSort(alist)
print(alist)

算法分析：

算法过程总需要n-1趟，随着趟数的增加，比对次数逐步从n-1减少到1，并包括可能发生的数据项交换。

比对次数是1～n-1的累加：
$$\frac{1}{2}{n}^2-\frac{1}{2}n$$
比对的时间复杂度是O(n²)

关于交换次数，最好的情况是列表在排序前已经有序，交换次数为0，最差的情况是每次比对都要进行交换，交换次数等于比对次数，平均情况则是最差情况的一半，时间复杂度也是O(n²)

选择排序（Selection Sort）：

选择排序对冒泡排序进行了改进，保留了其基本的多趟比对思路，每趟都使当前最大项就位。 但选择排序对交换进行了削减，相比起冒泡排序进行多次交换，每趟仅进行1次交换，记录最大项的所在位置，最后再跟本趟最后一项交换

程序代码：

def selectionSort(alist):
   for fillslot in range(len(alist)-1,0,-1):
       positionOfMax=0
       for location in range(1,fillslot+1):
           if alist[location]>alist[positionOfMax]:
               positionOfMax = location

       temp = alist[fillslot]
       alist[fillslot] = alist[positionOfMax]
       alist[positionOfMax] = temp

alist = [54,26,93,17,77,31,44,55,20]
selectionSort(alist)
print(alist)

算法分析：

选择排序的时间复杂度比冒泡排序稍优，比对次数不变，还是O(n²)，交换次数则减少为O(n)

四、插入排序算法及分析

插入排序（Insertion Sort）：

插入排序维持一个已排好序的子列表，其位置始终在列表的前部，然后逐步扩大这个子列表直到全表

• 第1趟，子列表仅包含第1个数据项，将第2个数据项作为“新项”插入到子列表的合适位置中，这样已排序的子列表就包含了2个数据项
• 第2趟，再继续将第3个数据项跟前2个数据项比对，并移动比自身大的数据项，空出位置来，以便加入到子列表中

经过n-1趟比对和插入，子列表扩展到全表，排序完成

程序代码：

def insertionSort(alist):
   for index in range(1,len(alist)):

     currentvalue = alist[index]
     position = index

     while position>0 and alist[position-1]>currentvalue:
         alist[position]=alist[position-1]
         position = position-1

     alist[position]=currentvalue

alist = [54,26,93,17,77,31,44,55,20]
insertionSort(alist)
print(alist)

算法分析：

插入排序的比对主要用来寻找“新项”的插入位置，最差情况是每趟都与子列表中所有项进行比对，总比对次数与冒泡排序相同，数量级仍是O(n²) ，最好情况，列表已经排好序的时候，每趟仅需1次比对，总次数是O(n)，平均情况时间复杂度为O(n²)

五、谢尔排序算法及分析

谢尔排序（Shell Sort）：

谢尔排序以插入排序作为基础，对无序表进行“间隔”划分子列表，每个子列表都执行插入排序

随着子列表的数量越来越少，无序表的整体越来越接近有序，从而减少整体排序的比对次数

最后一趟是标准的插入排序，但由于前面几趟已经将列表处理到接近有序，这一趟仅需少数几次移动即可完成

程序代码：

def shellSort(alist):
    sublistcount = len(alist)//2
    while sublistcount > 0:

      for startposition in range(sublistcount):
        gapInsertionSort(alist,startposition,sublistcount)

      print("After increments of size",sublistcount,
                                   "The list is",alist)

      sublistcount = sublistcount // 2

def gapInsertionSort(alist,start,gap):
    for i in range(start+gap,len(alist),gap):

        currentvalue = alist[i]
        position = i

        while position>=gap and alist[position-gap]>currentvalue:
            alist[position]=alist[position-gap] 
            position = position-gap

        alist[position]=currentvalue
        
alist = [54,26,93,17,77,31,44,55,20]
shellSort(alist)
print(alist)

算法分析：

粗看上去，谢尔排序以插入排序为基础，可能并不会比插入排序好

但由于每趟都使得列表更加接近有序，这过程会减少很多原先需要的“无效”比对，对谢尔排序的详尽分析比较复杂，大致说是介于O(n)和O(n²)之间

如果将间隔保持在2k-1(1、3、5、7、15、31等等），谢尔排序的时间复杂度约为O（n^3/2)

六、归并排序算法及分析

归并排序（Merge Sort）：

归并排序是递归算法，思路是将数据表持续分裂为两半，对两半分别进行归并排序

• 递归的基本结束条件是：数据表仅有1个数据项，自然是排好序的；
• 缩小规模：将数据表分裂为相等的两半，规模减为原来的二分之一；
• 调用自身：将两半分别调用自身排序，然后将分别排好序的两半进行归并，得到排好序的数据表

程序代码：

def mergeSort(alist):
    print("Splitting ",alist)
    if len(alist)>1:
        mid = len(alist)//2
        lefthalf = alist[:mid]
        righthalf = alist[mid:]

        mergeSort(lefthalf)
        mergeSort(righthalf)

        i=0
        j=0
        k=0
        while i<len(lefthalf) and j<len(righthalf):
            if lefthalf[i]<righthalf[j]:
                alist[k]=lefthalf[i]
                i=i+1
            else:
                alist[k]=righthalf[j]
                j=j+1
            k=k+1

        while i<len(lefthalf):
            alist[k]=lefthalf[i]
            i=i+1
            k=k+1

        while j<len(righthalf):
            alist[k]=righthalf[j]
            j=j+1
            k=k+1
    print("Merging ",alist)
    
alist = [54,26,93,17,77,31,44,55,20]
mergeSort(alist)
print(alist)

算法分析：

将归并排序分为两个过程来分析：分裂和归并

• 分裂的过程，借鉴二分查找中的分析结果，是对数复杂度，时间复杂度为O(log n)
• 归并的过程，相对于分裂的每个部分，其所有数据项都会被比较和放置一次，所以是线性复杂度，其时间复杂度是O(n)

综合考虑，每次分裂的部分都进行一次O(n)的数据项归并，总的时间复杂度是O(nlog n)

七、快速排序算法及分析

快速排序（Quick Sort）：

快速排序的思路是依据一个“中值”数据项来把数据表分为两半：小于中值的一半和大于中值的一半，然后每部分分别进行快速排序（递归）

快速排序的递归算法“递归三要素”如下：

• 基本结束条件：数据表仅有1个数据项，自然是排好序的
• 缩小规模：根据“中值”，将数据表分为两半，最好情况是相等规模的两半
• 调用自身：将两半分别调用自身进行排序（排序基本操作在分裂过程中）

程序代码：

def quickSort(alist):
   quickSortHelper(alist,0,len(alist)-1)

def quickSortHelper(alist,first,last):
   if first<last:

       splitpoint = partition(alist,first,last)

       quickSortHelper(alist,first,splitpoint-1)
       quickSortHelper(alist,splitpoint+1,last)


def partition(alist,first,last):
   pivotvalue = alist[first]

   leftmark = first+1
   rightmark = last

   done = False
   while not done:

       while leftmark <= rightmark and \
               alist[leftmark] <= pivotvalue:
           leftmark = leftmark + 1

       while alist[rightmark] >= pivotvalue and \
               rightmark >= leftmark:
           rightmark = rightmark -1

       if rightmark < leftmark:
           done = True
       else:
           temp = alist[leftmark]
           alist[leftmark] = alist[rightmark]
           alist[rightmark] = temp

   temp = alist[first]
   alist[first] = alist[rightmark]
   alist[rightmark] = temp


   return rightmark
   
alist = [54,26,93,17,77,31,44,55,20]
quickSort(alist)
print(alist)

算法分析：

快速排序过程分为两部分：分裂和移动

• 如果分裂总能把数据表分为相等的两部分，那么就是O(log n)的复杂度
• 而移动需要将每项都与中值进行比对，还是O(n)

综合起来就是O(nlog n)