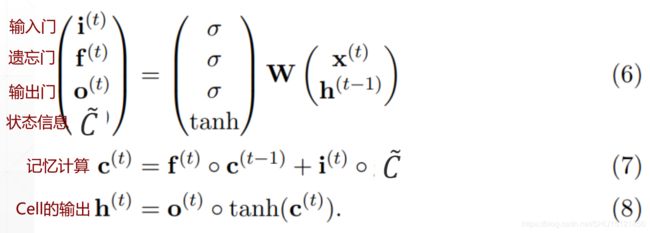【DL学习笔记】4:长短期记忆网络(Long Short-Term Memory)
在前面学习的循环网路中,因为梯度中有参数weight_hh的k次幂的存在,所以会导致梯度弥散和梯度爆炸的问题。对于梯度爆炸问题,可以用PyTorch笔记22最后面给出的梯度裁剪的方式解决。但是梯度弥散的问题没法这样直接解决,LSTM一定程度上解决了这样的问题,从而为长序列记忆提供了较好的解决方案。
长序列难题
在原始的循环网络中,实际上能处理的记忆信息比较短。如对自然语言的处理中,只能记住之前较少的几个单词的语境信息。例如"The clouds are in the sky"其中可以由"clouds"预测出"sky",它们之间的时刻比较接近。
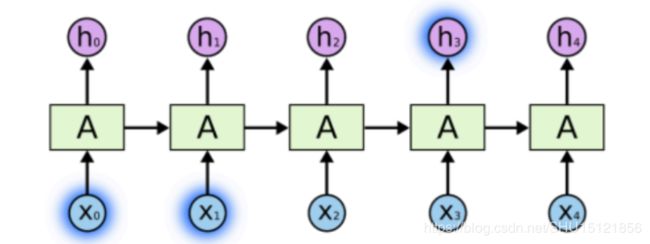
但是循环网络很难从"I grew up in France… I speak fluent"预测出下一个词是"French",因为中间还有太多的单词,这就是长序列难题。LSTM就可以更好的处理长序列问题,其中STM三个字母就表示在循环网络中的记忆单元Short-Term Memory,它表示只能做短期的记忆,而LSTM的含义就是把记忆单元的短记忆延长了,所以前面加个单词Long。
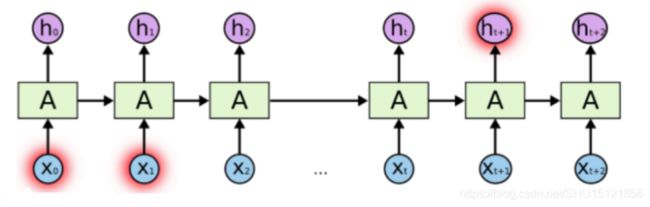
回顾循环网络的结构
在前面学的循环网络中,只是单纯的将上次处理完的记忆单元和当前输入经线性变换后加在一起,再直接用Tanh反曲正切激活:
h t = T a n h ( W h h ⋅ h t − 1 + W t h ⋅ x t + b ) h_t = Tanh(W_{hh} \cdot h_{t-1}+W_{th} \cdot x_t+b) ht=Tanh(Whh⋅ht−1+Wth⋅xt+b)
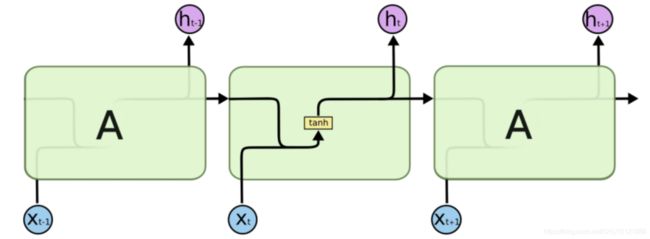
它还可以表示成之前的隐含单元 h i − t h_{i-t} hi−t和当前输入 x t x_t xt经组合后由一个大的线性变换矩阵处理,再进行Tanh激活:
h t = T a n h ( W ⋅ [ h t − 1 , x t ] + b ) h_t = Tanh(W \cdot [h_{t-1},x_t]+b) ht=Tanh(W⋅[ht−1,xt]+b)
这个表达方式对后面LSTM的前向计算描述很重要。
LSTM的门控思想
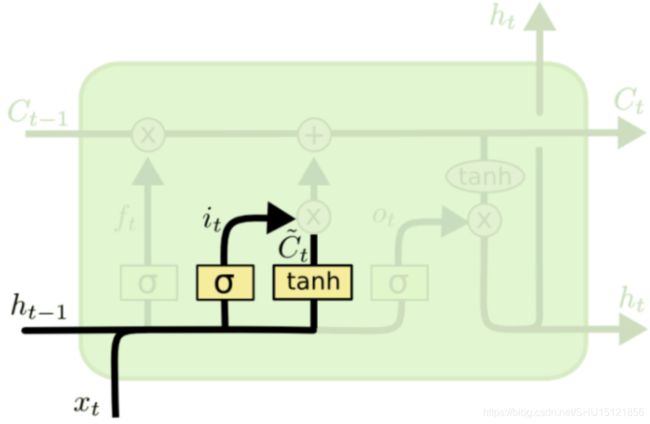
在数字电路中,门只有0和1两种状态。直观来看,LSTM的门控也是将信息有目的的过滤,为了取0倍到1倍之间的连续值,采用sigmoid值来和信息进行element-wise相乘。而这样的门控机制在旧的记忆信息、新输入的信息、输出信息时都要做。在图中可以看到圈出来的 σ \sigma σ的地方就是门控的地方:
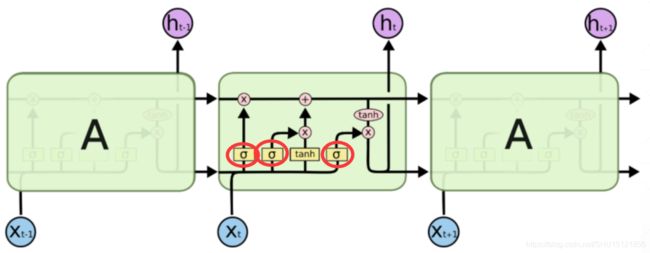
而门控的sigmoid值作为流量控制量——开度,显然也需要由网络自己学习得到,所以sigmoid的输入设计成网络此时的状态即 x t x_t xt和 h t − 1 h_{t-1} ht−1的组合变换:
σ = s i g m o i d ( W ⋅ [ h t − 1 , x t ] + b ) \sigma = sigmoid(W \cdot [h_{t-1},x_t]+b) σ=sigmoid(W⋅[ht−1,xt]+b)
注意,图中可以看到有两条水平的、沿着时间轴传递的通道,其中上面一条传递的是C,它才是LSTM中的"记忆",而下面传递的是是循环网络中也有的h,它是一种"隐含状态"的表示,同时也是LSTM的输出。
遗忘门(Forget gate)
因为 σ \sigma σ越大乘下来之后信息保留的就越多,遗忘门实际上应该叫"记忆门"更符合语义一些。门的开度还是(三个门公式都是一样的,但参数互不影响):
f t = s i g m o i d ( W f ⋅ [ h t − 1 , x t ] + b f ) f_t = sigmoid(W_f \cdot [h_{t-1},x_t]+b_f) ft=sigmoid(Wf⋅[ht−1,xt]+bf)
遗忘门控制的的是上一次层传进来的的记忆信息 C t − 1 C_{t-1} Ct−1,如图所示:
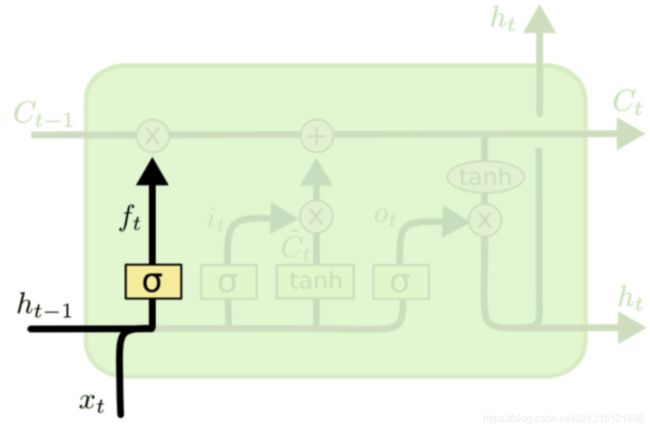
输入门(Input gate)
输入门处理的是这一层输入的"Cell State",并不是单纯的处理输入 x t x_t xt,而是处理像循环网络中的和隐藏单元聚合后做Tanh激活后的状态信息:
C t ~ = T a n h ( W C ⋅ [ h t − 1 , x t ] + b C ) \tilde{C_t} = Tanh(W_C \cdot [h_{t-1},x_t]+b_C) Ct~=Tanh(WC⋅[ht−1,xt]+bC)
输入门开度的计算还是:
i t = s i g m o i d ( W i ⋅ [ h t − 1 , x t ] + b i ) i_t = sigmoid(W_i \cdot [h_{t-1},x_t]+b_i) it=sigmoid(Wi⋅[ht−1,xt]+bi)
新的记忆信息的计算
将当前的遗忘门开度 f t f_t ft作用在上一层的记忆信息 C t − 1 C_{t-1} Ct−1上,将当前的输入门开度 i t i_t it作用在当前状态信息 C t ~ \tilde{C_t} Ct~上,然后将它们相加,即得到当前Cell的记忆信息 C t C_t Ct:
C t = f t ⋅ C t − 1 + i t ⋅ C t ~ C_t = f_t \cdot C_{t-1} + i_t \cdot \tilde{C_t} Ct=ft⋅Ct−1+it⋅Ct~
输出门(Output gate)
之所以先说记忆 C t C_t Ct的计算,是因为输出门是建立在记忆计算完成的基础上的,具体地,是将记忆 C t C_t Ct进行Tanh激活之后,再用输出门 o t o_t ot对其进行限制,得到本时刻的输出(即隐含状态) h t h_t ht:
h t = o t ⋅ T a n h ( C t ) h_t = o_t \cdot Tanh(C_t) ht=ot⋅Tanh(Ct)
其中输出门开度的计算同样是:
o t = s i g m o i d ( W o ⋅ [ h t − 1 , x t ] + b o ) o_t = sigmoid(W_o \cdot [h_{t-1},x_t]+b_o) ot=sigmoid(Wo⋅[ht−1,xt]+bo)
如图所示:
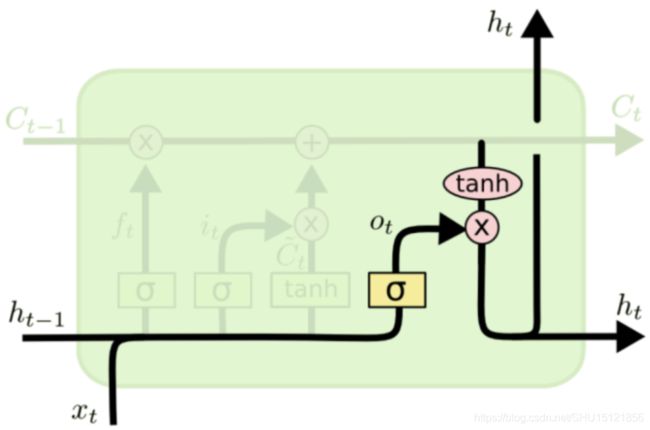
注意,图中 h t h_t ht除了向右输出还向上输出的原因是LSTM也可以有多层,当有多层时,本层的输入就是上一层对应时刻输出的 h t h_t ht。另外要注意,与之不同的是,记忆 C t C_t Ct只能沿着时间线横向传播。
总结
对LSTM门控机制的直观而极端的理解(说这是一种极端的理解,因为门是取连续值的,而不是像数字电路一样取离散值):

当输入门关闭,遗忘门全开时,即是完全取用上一时刻的记忆不变。
当输入门和遗忘门都全开时,即是将上一时刻的记忆加到这一时刻的状态上,完全综合两者信息。
当输入门和遗忘门都完全关闭时,即是不取用任何信息,相当于在这一时刻"失忆"+"关闭一切感官。
当输入门全开,遗忘门完全关闭时,即是完全依靠现有的信息和隐含状态,而丢掉之前的记忆信息。
最后是关于为什么LSTM能解决梯度弥散的问题。循环网络中会发生梯度弥散,是因为相邻时刻的梯度是这样的形式:
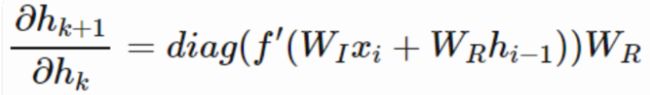
其中 W R W_R WR就是之前学的 W h h W_hh Whh,所以层数多了之后,链式法则相乘会有一堆 W h h W_{hh} Whh乘在一起:
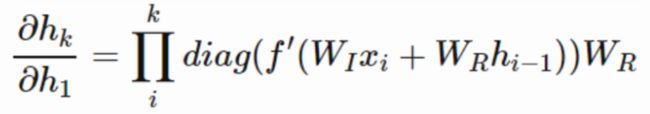
而循环网络完全没法保证这些 W h h W_hh Whh不会都小于1,也就没法避免梯度弥散了。
对于LSTM而言,相邻时刻的梯度是这样的:

可以看到是若干项相加的形式,这样加起来仍然小于1的概率就小了很多了,从而不容易发生梯度弥散。