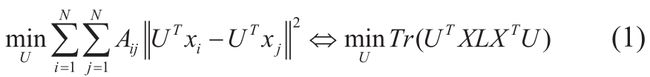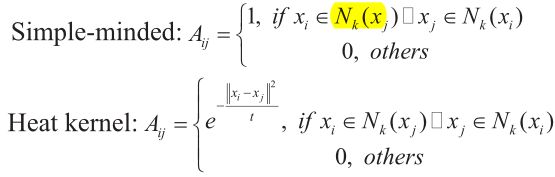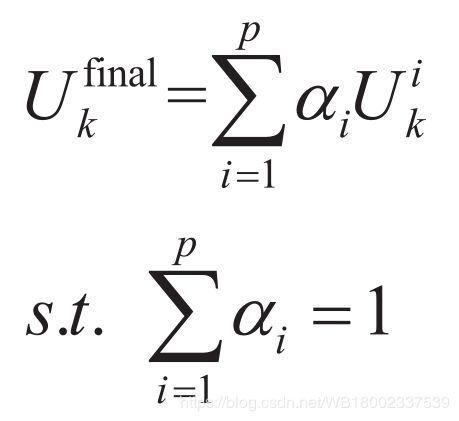WLDPP（ Weighted Local Discriminant Preservation Projection Embedded Ensemble Algorithm）局部判别保留投影法

本文主要介绍一下论文《Recognition algorithm of Parkinsons disease based on weighted local discriminant preservation projection embedded ensemble algorithm》中针对帕金森疾病数据提出的 WLDPP（局部判别保留投影法） 方法

---

一、 基本介绍

目前帕金森病数据的问题是高冗余、高噪声和小样本，降维可以有效地解决这些问题。本文提出了一种加权局部判别保持投影嵌入集成算法，与现有的特征选择和特征提取算法相比，能显著提高帕金森病的诊断准确率。

降维是指利用映射方法将原始高维空间中的数据点映射到低维空间。降维方法可分为特征选择和特征提取，从初始特征空间中提取最优特征子集。根据评价函数，特征选择方法可分为三种类型：

• 过滤：按照发散性或者相关性对各个特征进行评分，设定阈值或者待选择阈值的个数，选择特征。
• 包装：根据目标函数（通常是预测效果评分），每次选择若干特征，或者排除若干特征。
• 嵌入：先使用某些机器学习的算法和模型进行训练，得到各个特征的权值系数，根据系数从大到小选择特征（类似于Filter方法，但是是通过训练来确定特征的优劣）。

LPP（局部保留投影法）是流形降维的典型代表算法，它最有效地保留了数据集的邻域结构，但LPP算法仍然存在一些缺点：

• 1）首先，它对邻域样本数比较敏感。
• 2）其次，LPP存在小样本问题，即当维数大于样本数时，数据矩阵变为奇异。

改进的LPP方法仍然忽略了一些问题：

• 1）大多数基于LPP的改进算法只关注增加类之间的方差，而没有考虑类内方差较大的数据集。
• 2）算法在映射高维数据时缺乏稳定性（小样本数据集的划分具有很大的随机性，当训练数据和测试数据之间的数据分布存在差异时，预测学习者的结果可能会降低）。

---

二、 算法步骤

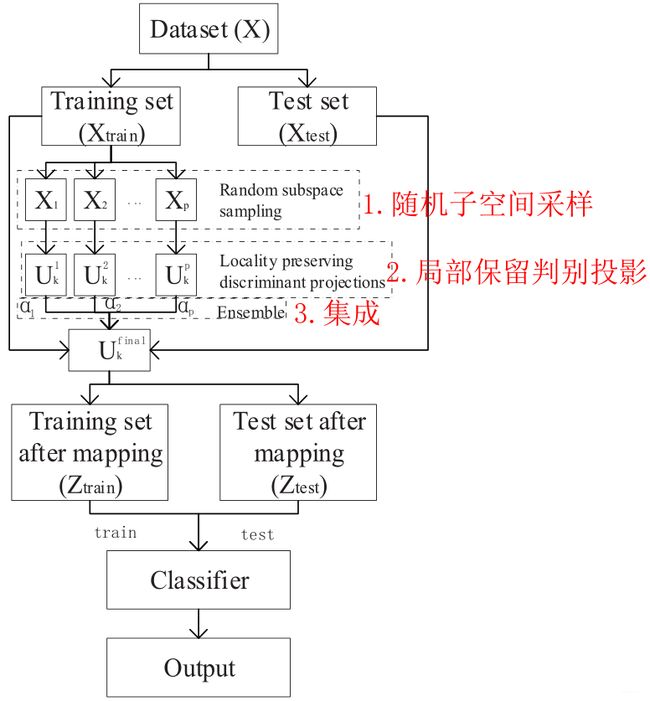
WLDPP基本思想为在保留LPP局部性的前提下，最小化局部类内散射矩阵的迹，最大化类间散射矩阵。算法流程图如下图所示，主要由3部分组成：

• 1）对训练数据进行随机子空间采样；
• 2） 基于所提出的目标函数建立了局部保留的判别投影；
• 3）利用集成学习构造最终的映射矩阵。

1. 随机子空间采样

2. 局部保留判别投影

LPP的目标是最优地保持数据的邻域结构，其目标函数使原始数据空间中具有邻域关系的数据点之间的距离最小（即局部保留）。局部保留可被描述为：

$L=D-A$ 为拉普拉斯矩阵，$D_{ii}={\sum }_j{A}_{ij}$为对角阵，A为亲和度矩阵，计算公式如下：

提出的WLDPP可被描述为：
$S_B={\sum }_{c=1}^C{N}_c({\mu }_c-\mu )({\mu }_c-\mu {)}^T$ 为类间散射矩阵，$S_w={\sum }_{c=1}^C{\sum }_{x\in X_c(X^{(c)}-{\mu }_c)(X^{(c)}-{\mu }_c{)}^T}$ 为类内散射矩阵，$\mu =\frac{1}{N}{\sum }_{i=1}^N{x}_i$ 为 $X$ 的中心，${\mu }_c=\frac{1}{N}{\sum }_{i=1}^{N_c}{x}_i$ 为 $X$ 中第 $c$ 类的中心，$x^{(c)}$ 为 $X$ 中的第 $c$ 类样本，对 $U$ 进行求导得到最优解

通过上式，投影矩阵 $U$ 可轻易得到，向量 $U_k=(u_1,u_2,...,u_k)$ 为 $U$ 的前 $k$ 个特征向量，然后，将原始高维数据投影到由 $U$ 列构成的低维空间上，实现降维。

3. 集成

利用集成学习构造最终的映射矩阵。局部保持判别投影算法重复 $p$ 次，分别输出 $U_k^1,U_k^2,...,U_k^p$，最终映射矩阵 $U_k^{final}$ 由 $U_k^i,(i=1,2,...,p)$ 加权后获得，即

$\alpha$ 是一个由网格搜索发得到的加权因子。