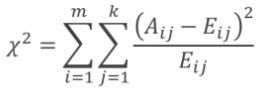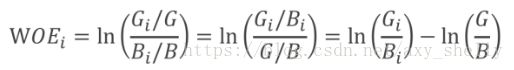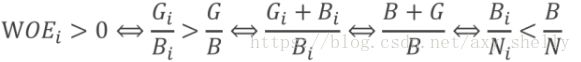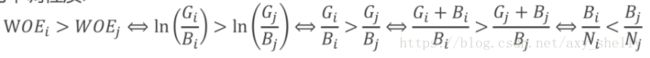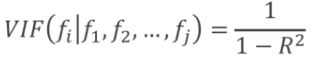评分卡模型 数据预处理与特征构建

一、数据预处理、特征构建

预处理：处理缺失值、异常值，增强模型的稳健性

特征构建：形成有业务含义的优异特征

1. 评分卡模型

（1）分类和特征

- 风控场景中的评分卡：反欺诈评分卡、申请评分卡、行为评分卡、催收评分卡

- 以分数形式来衡量风险几率的一种手段

- 对未来一段时间内违约/逾期/失联概率的预测

- 有一个明确的（正）区间

- 通常分数越高越安全

- 数据驱动

- 非信贷场景中的评分卡：推荐评分卡、流失评分卡

（2）开发步骤

- 立项：确定场景、产品和人群

- 数据准备与处理：选取数据、清洗数据、特征工程

- 模型构建：参数估计

- 模型评估：性能测试

- 验证/审计：验证建模的合理性

- 模型部署：上线

- 模型监控：持续监控并优化

（3）常用模型

2. 数据集介绍

「拍拍贷信贷申请审核」竞赛数据集

- 查看数据集基本信息、关键字段的含义和缺失值

- 特征构造的方法：求和、比例、频率、平均

- 什么是好的特征

- 稳定性高：内外部环境稳定时，特征的分布也要稳定

- 区分度高：未来的违约与非违约人群在特征上的分布需要显著不同

- 差异性大：不能对全部人群或绝大部分人群上有单一的取值

- 符合业务逻辑：特征与信用风险的关联关系要符合风控业务逻辑

3. 特征构建的方法

- 类别变量不能求和、平均、最值等，可以求频率和个数（不同时间切片）

- 时间切片太长，大部分样本的时间跨度无法满足

- 时间切片太短，抓取不到足够多的信息，且变量不稳定

- 通过计算登录日期与放款日期之间的间隔天数，可以看到绝大部分的天数在180天以内

- 时间切片选择：30、60、90、120、150、180

- 计算逻辑：针对idx在时间切片内的（注意消除线性相关性对模型产生的影响）

- 登陆次数

- 不同登录方式的个数

- 不同登录方式的平均个数

4. 数据的质量检验与处理

（1）数据集中度

在变量中，某单一数值的占比占了全部样本值的绝大多数（如学历）。

具有极高的集中度的字段或变量，需要按照风险程度（坏样本率：违约率）进行区分：

- “多数值”与“少数值”对应的坏样本率没有显著差别

- 包含信息较少，对模型开发没有太大价值

- 少数值的产生往往由于误差或者噪声，可以直接将字段删除

- 有显著差别，且坏样本率“少数值”<“多数值”

- 更关注风险高的一组，所以少数值得存在并不会带来额外的意义

- 直接将字段删除

- 有显著差别，且坏样本率“少数值”>“多数值”

- 少数值得存在表明该值对应的风险很高，字段需要保留

tips：10的对数是2.303，1/10的对数是-2.303，可以利用这个来比较比率，更直观

（2）数据缺失

数据缺失的两个维度：

• 字段维度：某个字段在全部样本上的缺失值个数的占比

• 样本维度：某条样本在所有字段上的缺失值的占比

缺失机制不同，处理方法也不同：

• 完全非随机缺失：有缺失的样本的违约率显著高于无缺失样本

• 完全随机缺失：有缺失的样本的违约率与无缺失样本无明显差异

  • 如果缺失样本的占比很少，可将样本删除

  • 如果缺失样本的占比较高，需要将字段删除

处理方法：

• 舍弃该字段或该条记录：缺失占比太高

• 补缺：缺失占比不高（前提，否则会产生较大的偏差），可用均值法、众数法、回归法等

  • 数值型变量：均值法（完全随机缺失）、抽样法（完全随机缺失）、回归法（针对随机缺失）

  • 类别型变量：抽样法，众数法

• 作为特殊值（通常做法）：将缺失堪称一种特殊值（划分为单独的箱）

判断变量类型的准则：

• 当且仅当变量取值为数值，且不同值的个数比较多时，视为数值型变量

• 其他情况下均视为类别型变量

（3）异常值（outliners）

判断：聚类法、分位点法

处理：删除、替换

注意：某些异常值可能有特殊意义，如PBOC征信记录查询次数过多，很有可能申请人资金需求迫切，未来逾期概率可能会较高。这样的数据不宜删除或用正常值替换。需要用其他的方法（比如与其他值合并作为一个箱）

（4）数据含义一致性

不一致的原因：录入时对于同一含义的值做了不同记录，一般是大小写的区别、空格或特殊符号等

此时要将数据替换为一致的

目标：建立Logistic Regression的特征必须是数值型

所以：需要对类别型变量进行编码

 

and：

       1. 建模时，为了获取评分模型的稳定性，需要对数值型特征做分箱处理

1. 代入模型之前，需要对特征做单变量与多变量分析的工作

 

 

一、特征的分箱

什么是分箱：

• 数值型变量：分成若干有限的几个分段

• 类别型变量：如果取值个数很多，将其合并为个数较少的几个分段

为什么要分箱：

• 评分结果需要有一定的稳定性

  • 当借款人的总体信用资质不变时，评分结果也应保持稳定

  • 例如：月收入从6k变为7k，在其他因素不变的情况下，评分结果也不会发生改变

• 类别型变量，当取值个数很多时，如果不分箱，会导致变量膨胀

  • n个城市，使用onehot会产生n个变量，采用哑变量编码会产生n-1个变量

分箱的要求：

• 不需要分箱的变量：取值个数较少的类别型变量

• 分箱结果

  • 有序性：对于有序型变量（包括数值型-工资、有序离散型-学历）

  • 平衡性：（严格情况）每一项的占比不能相差太大，一般要求占比最小的不低于5%

  • 单调性：（严格情况）有序型变量分箱后每箱的坏样本率要求与箱呈单调关系

  • 个数：在5或7个以内

分箱的优缺点：

• 优点

  • 稳定：分箱后，变量原始值在啊一定范围内的波动不会影响到评分结果

  • 缺失值/异常值处理：缺失值可以作为一个单独的箱，或者与其他值进行合并作为一个箱

  • 无需归一化：从数值型变成类别型，没有尺度差异

• 缺点

  • 有一定的信息丢失

  • 需要编码：类别型不能直接带入逻辑回归模型中，需要进行一次数值编码

常用的分箱方法：

分箱的初衷：将相似度高的样本归为一组

• 有监督分箱：考虑的是特征业务含义的相似度

  • 方法：

    • 卡方分箱法：以卡方分布和卡方值为基础，判断某个因素是否会影响目标变量（卡方检验：性别是否会影响违约概率）

      • 适用于数值型变量（具体方法见下文）

      • 如果变量是类别型的，也可以用卡方分箱法

        • 无序且取值个数较大（省份）

          • • 解决方法：分箱前进行一次数值编码，用数字代替类别型值。常用的数值编码是该数值对应的平均坏样本率

          • 例如：用每个省在样本里的坏样本率代替省级行政区

        • 有序（学历）

          • 解决方法：先排序，然后按照数值高低替换，进行分箱

      • 优点

        • 解释性强：有很强的统计意义

        • 能够解决多分类场景的分箱：对类别数没有限制，适用于二分类、多分类

      • 缺点：计算量大，需要对数值型变量先做离散，然后迭代地选择最优分箱法

        • 假设原变量先离散成p个区间，最后合并为q个区间，则需要计算(p-1)(p+q-1)/2个卡方值决策树分箱法

  • 优点：与目标变量结合，最大程度低将目标变量的信息反映在特征中

  • 缺点：计算量大

• 无监督分箱：考虑的是特征在样本上的分布的相似度

  • 方法：

    • 等距

    • 等频

    • 聚类

  • 优点：计算简单

  • 缺点

    • 合理性得不到保证

    • 不能充分利用目标变量的信息

带有特殊值（如缺失）的分箱：

连续型变量的分箱工作需要预先将这些特殊值排除在外，即特殊值不参与分箱，看成单独的一箱，其他正常值参与分箱。分箱个数=预设个数-特殊值个数

• 检验坏样本率的单调性时，不考虑特殊值的坏样本率（特殊值无法和其他数值进行比较）

• 特殊值占比较小（低于5%）时，考虑将特殊值与正常值中的一箱进行合并（通常与最小的or最大的）

卡方检验：判断某个因素是否会影响目标变量   H0假设： 观察频数与期望频数没有差别，即，该因素不会影响目标变量 x2：表示观察值与理论值之间的偏差程度。 就是用（期望-实际）^2/期望，把所有值加在一起 m：该因素的取值个数 k：类别数 自由度：(m-1)*(k-1)   根据x2分布和自由度，可以确定，在H0假设成立的情况下，获得当前统计量甚至更极端情况的概率P   if：p很小，说明观察值与理论值偏离程度太大，应拒绝H0；该因素下的m种类别有显著差异   if：p值大于预期水平，那么，不能拒绝H0，该因素不会影响到目标变量

卡方分箱法：采取自底向上不断合并的方法，在每一步的合并过程中，依靠最小的卡方值来寻找最优的合并项。 核心思想：如果某两个区间可以被合并，那么两个区间的坏样本需要有最接近的分布，进而意味着两个区间的卡方值时最小的 终止条件（1、2通用，3、4评分卡）： 某次合并后，最小的卡放置的p值超过0.9（或0.95、0.99） 某从合并后，总的未合并的区间数达到指定的数目（如5、10、15） 每箱的坏样本率单调（分箱后，具有风控业务含义） 如果不满足，需要选择相邻的箱进行合并，知道满足为止 如果有多重合并的方式，可按照某种准则挑选最优的合并方案 方案1：利用卡方分箱法缩减分箱数目（重新设定分箱数，检验单调性） 当分箱数只有2箱的情况下，单调性的存在性失去意义 方案2：对于当前不满足单调性的箱，与之前或之后的箱合并。合并原则： 合并之后，非单调的程度减轻 如果两种方案都可以减轻非但单调性，可以选择“较优”的一种。较优的含义： 合并后，卡方值更低的 合并后，所有箱的占比更加平衡的 即判断分箱后的分布均匀性，balance越小越均匀 原变量分为m箱，各箱占比为pi，则balance等于各箱占比的平方和 当pi都等于1/m时，balance最小 当pi中有一个为1，其余为0时，balance最大 只有某些变量，坏样本率的非单调性有一定的业务含义，允许保留U型/倒U型的坏样本率 每箱同时包含好、坏样本（为了能计算WOE） 如果不满足，需要和相邻的某一箱合并，选择左or右，同样由较小的卡方值决定 步骤： 将数值变量A排序后分成区间较多的若干组，设为A1,A2,...,An 计算A1,A2合并后的卡方值，A2,A3，直至A(n-1),An 找出上一步所有合并后的卡方值中最小的一个，假设为A(i-1),Ai，将其合并形成新的A(i-1) 不断重复2、3，直至满足终止条件

二、WOE与特征信息值

编码：用数值代替非数值（例如，用3组0~255之间的整数对颜色进行编码）

目的：让模型能够对其进行数学运算

 

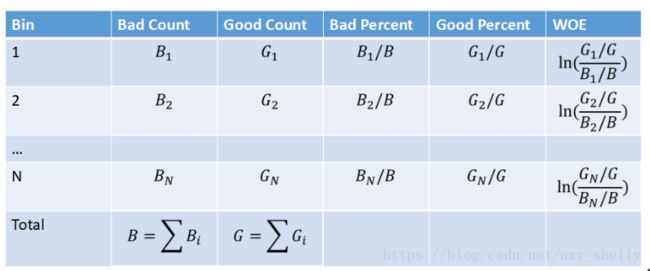
WOE（Weight of Evidence）编码：

WOE公式：

1. WOE的符号性质：

        如果某箱的WOE是正的，表明该箱的坏样本率低于整个样本的平均坏样本率。即，相对更加容易出现好样本

        

1. WOE的单调性质：WOE的单调性与坏样本率的单调性相反

        

注意点：

1. Gi和Bi必须为大于0的正数，这样才能使某一箱的WOEi都有意义。因此，分箱时每一箱都必须同时包含好坏样本

2. 分子、分母可以反过来，但是同一个模型里，所有变量的处理方式是一致的。

3. WOE的计算方式对后续Logistic Regression模型的变量的符号是有一定要求的（？啥要求）

优点：

• 提高模型的性能：能够提高模型的预测精度（以每一箱中的相对全体的log odds的超出作为编码依据）

• 统一变量的尺度：一般为[-4,4]

• 分层抽样的WOE不变性：如果建模需要对好坏样本进行分层抽样，则抽样后计算的WOE与未抽样计算的WOE是一致的

缺点：

• 要求每箱中同时包含好坏样本：

• 对多类别标签无效：如果目标变量取值个数超过2个，分箱后的WOE是无法计算的

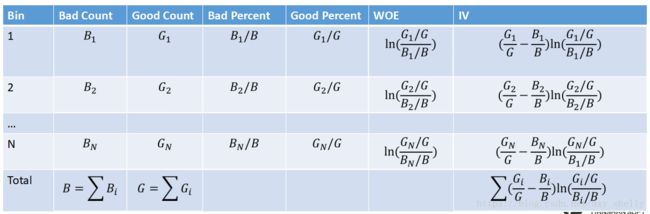
特征信息值（IV）：

衡量变量重要性，挑选出相对更加重要的变量，为后续的分析提供降维的能力。

特征信息值（Information Value）的计算公式：

IV是WOE的加权，权重是(Gi/G-Bi/B)。如果WOE的计算分子、分母相反，则权重也相反。

IV的性质：

1. 非负性

2. 权重性：WOE反映的是每箱中好坏比相对全体样本好坏比的超出（excess），IV反映的是该箱体量的意义下，这种超出的显著性

        如：A1箱好坏各占2%、1%，A2箱好坏各占20%、10%

• • WOE角度：二者一致，都是ln2

  • IV角度：前者体量2%-1%，后者体量20%-10%，后者的显著性更强一点

注意：

1. IV衡量的是特征总体的重要性，而非每一箱的重要性

   • IV越大，该变量的重要程度越高

   • IV值不宜太大，否则有过拟合的风险

2. 与WOE一样，IV也要求每一箱中同时包含好坏样本

3. IV不仅受到变量重要性的影响，同时也与分箱方式有关（所以要注意分箱的合理性）

   • 一个变量分箱粒度越细，IV会升高

   • 若干个变量分箱的个数差异不大时，才能比较IV

三、单变量分析与多变量分析

单变量分析（Single Facotr Analysis）：

通常先选择IV高于阈值（如0.2）的变量，然后再挑选出分箱较均匀的变量

1. 变量的重要性（IV）：当IV异常高（如超过1），此时变量的分箱方式可能是不稳定的

• • >=0.2：有较高的重要性

  • 0.1~0.2：有较弱的重要性

  • <0.1：几乎没有重要性

1. 变量分布的稳定性：合适的变量，各箱占比不会很悬殊。

   • 如果有一箱的占比远低于其他箱，那该变量的稳定性也较弱

多变量分析（Multi Facotr Analysis）：

完成单变量分析，利用多变量分析进一步缩减变量规模，需要对变量的整体性做把控，形成全局更优的变量体系。

主要从两个角度分析变量特性并挑选：

• 变量间的两两线性相关性

  • 不允许存在，原因如下

    • 说明变量间存在一定的信息冗余，没必要保留，会增加模型开发、部署与维护的负担

    • 影响回归模型的参数估计，产生较大偏差

  • 判断方法：相关性矩阵

  • 解决方法：保留IV值较高的一个

  • 处理流程：

    1. 将变量按照IV进行降序排列f1,f2,...,fp

    2. 令i=1，计算(fi,fi+1),(fi,fi+2)....(fi,fp)的相关系数

    3. 如果（fi,fj）相关系数较大，则剔除fj（相关系数通常用较高的阈值来对比，比如0.7~0.9之间的数）

    4. 令i=i+1

    5. 重复2~4步骤，知道剩余变量中不存在较高的线性相关性

• 变量间的多重共线性（multicolinearity）

  • 多重共线性：一组变量中，某一个变量与其他变量的线性组合存在较强的相关性

  • 不允许存在的原因同线性相关性

  • 衡量：方差膨胀因子（VIF）

    • R^2是f1,f2,...,fi对fi的线性回归的决定系数

    • 一般用10来衡量。VIF>10，认为变量间存在多重共线性

    • • 逐步从f1,f2,...,fj剔除一个变量，剩余的变量与fi计算VIF

      • 若剔除fk后，VIF<10

        • 从fi与fk中剔除IV较低的一个

      • 若每次剔除一个变量不能降低VIF，则每次剔除2个变量，直至变量间不存在多重共线性